MO TST 2021部分题目题解

D3T2

题意：

题解：

不难想到答案应该差不多是\(\frac{k}2\)左右，且应该越密集越好，也就是\(kn+1\)的完全图。

也就是说有\(n\)个组，其中有\(n-1\)个组有\(k\)个点，有一个组有\(k+1\)个点，两两间都有边。

答案可以很容易算出来是：

\[\frac{n\binom{k}{2}+k}{nk+1} \]

证明：

用到神仙的概率证明：

考虑一个\(m\)个点的图，我们随机地将这\(m\)个点排成一行：\(p_1,p_2...p_m\)。

我们从前到后贪心地分配颜色：颜色为左边相连的个数最少的颜色。

设\(S(i)\)表示\(i\)连向左边的边数，可以发现贡献最多是\(\lfloor\frac{S(i)}{n}\rfloor\)。

最终只需要计算：

\[E(\sum_{i=1}^m \lfloor \frac{S(i)}n\rfloor)=\sum_{i=1}^{kn}\lfloor \frac{i}{n} \rfloor \times E([v:\{S(v)=i\}]) \]

设\(F(i)=E([v:\{S(v)=i\}]\)。

显而易见\(F(i)=m\times \frac{1}{kn+1}\)。

所以直接带进去算一下得到:

\[E=\frac{m}{kn+1}\times \sum _{i=0}^{kn}=\frac{n\binom{k}{2}+k}{nk+1}\times m \]

非常amazing!

刚好就是上面的值，证毕。

D4T2

题意：

题解：

可以将满足要求的段在图中画出来：

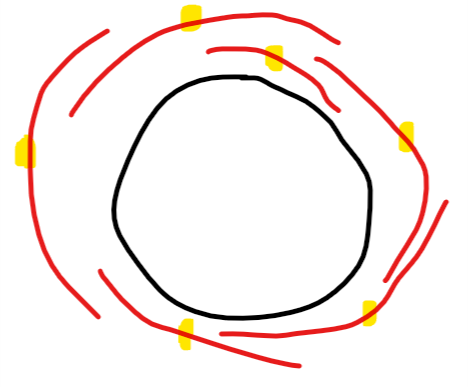
设这些段的集合为\(A_i\),其中黄色的点为中点。

满足条件的\(b_k\)的个数也就是黄色点的个数。

其中黄色点的个数又\(\leq\)所有\(A_i\)的并的大小。

可以列出式子：

\(k\leq |\bigcup_{i=1}^kA_i|\)，其中\(k\)为\(b_i\geq1\)的下标的个数。

同时对\(\{A_1,A_2...A_k\}\)做一些调整，删除一些不必要的集合使得并不变。

假设删成了\({A_{i_1},A_{i_2},A_{i_3}...A_{i_s}}\),其中\(s\)时极小的。

可以发现这些段满足以下性质：
任意间隔为二的段不交，将环展开大概这样，同时也可以发现任意一个位置最多会被覆盖2次：

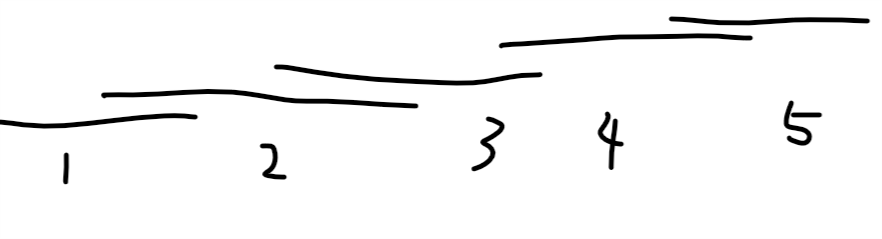
也就是：

\(k\leq |\bigcup_{i=1}^kA_i|=|\bigcup_{j=1}^sA_{i_j}|\)。

其实我们还有一个条件没有用，就是\(b_k\geq1\)，翻译过来就是段的平均数\(\geq 1\)。

也就是说\(A_i\leq \sum _{x\in A_i} a_x\)。

所以：

\(k\leq |\bigcup_{i=1}^kA_i|=|\bigcup_{j=1}^sA_{i_j}|\leq \sum _{j=1}^s\sum _{x\in A_{i_j}}a_x\leq 2\sum_{i=1}^{2n+1} a_i\)。

D2T3

题意：

A,B在轮流玩一个游戏：初始黑板上有\((n+1)^r\)个数字:\(\prod p_i^{a_i} ,(0\leq a_i\leq n)\) ,\(p_i\)为互不相同的质数。

A的操作： 擦掉\(a,b\)，写上\((a,b)\),也就是\(\gcd (a,b)\)

B的操作： 擦掉\(a,b\)，写上\([a,b]\),也就是\(\text{lcm}(a,b)\)

\(A\)要使最后的数尽可能小，\(B\)要使最后的数尽可能大，求最后的数是多少。

题解：

设\(M=\prod p_i\)，可以很容易猜到答案\(Ans=M^{\lfloor \frac{n}2\rfloor}\)。

设剩下的数为\(X\),下面证明\(A\)可以保证\(X|Ans\),且\(B\)可以保证\(Ans|X\)。

个数的奇偶性不同，两个人的策略是不同的：

1. n是奇数，黑板上的数的个数为偶数，一定是A走完最后一步
2. n是偶数，黑板上的数的个数为奇数，一定是A走完还剩两个数

当n是奇数时A的策略

第一步，A执行操作\((1,M^n)\)，令\(\alpha=(1,M^n)=1\)

考虑\(B\)的操作:

1. \([x,M^n/x]\),则A可以执行\((\alpha,[x,M^n/x])\),由于\(\alpha|[x,M^n/x]\),这样可以除去添加的\([x,M^n/x]\),所以一个回合本质上少了\(x\)和\(M^n/x\)两个数。
2. \([x,y],x,y\neq \alpha,xy\neq M\),则A执行操作\((M^n/x,M^n/y)\),可以发现\((M^n/x,M^n/y)\cdot [x,y]=M^n\)。
3. 否则B的操作形如\([\alpha,x]\)，假设\(Ans|x\)(否则可以把\(x\)变成\(Ans\),这样并不会使\(B\)的操作边劣，同时也不会影响到A),则这个操作实质上是除去了\(\alpha\),由于\(\alpha|Ans\)。然后A可以直接操作\((x,M^n/x)\),然后令\(\alpha = (x,M^n/x)\)。

分析A的操作，可以发现每时每刻\(\alpha\)一定是存在黑板上的。同时对于任意的\(x|Ans\)，\(x\)的个数一定是\(\geq M^n/x\)的个数的，其中\(\alpha\)的个数一定\(>M^n/\alpha\)的个数，但是根据操作3，A并没有删除\(\alpha\),所以其它的\(x,(满足x|Ans)\)的个数任然可能\(>M^n/x\)的个数。同时\(\alpha|Ans\),所以A可以在黑板上保留一个Ans的因子。

当n是偶数时A的策略

这时候A会在黑板上剩下两个数\(\alpha,\beta\)。我们需要使得\([\alpha,\beta]|Ans\)，下面我们证明A可以保证\(\alpha,\beta|Ans\)。

第一步,A执行操作\((1,M^n)\),令\(\alpha =1,\beta=Ans\)。

考虑B的操作：

1. \([x,y],(x,y\neq \beta)\)。则A可以按照n是奇数的规则，因为不会影响到\(\beta\),只需要保证\(\alpha|Ans\)即可。
2. \([\alpha ,\beta]\)，则A执行操作\((x,M^n/x)\)，令\(\beta=[\alpha,\beta],\alpha=(x,M^n/x)\)，\(x\)是任意数。这样只会消除\(x,M^n/x,\alpha,\beta\)（\(\alpha,\beta\)都是原来的）。
3. \([\beta,x],x\neq \alpha\),则A执行操作\(([\beta,x],M^n/x)\),令\(\beta=([\beta,x],M^n/x)\)。

得到的结论和上面差不多，剩下两个数\(\alpha,\beta\)都满足是\(Ans\)的因子。

当n是偶数时B的策略

初始令\(\alpha = Ans\)。

可以发现B可以完全照抄A在n是奇数是的策略，只需要将\(x\)看作\(M^n/x\)，然后两方的操作就反过来了。

也就是B可以保证剩下的数\(\alpha|Ans\)，也就是\(Ans|M^n/\alpha\)。

当n是奇数时B的策略

也和A在偶数的时候的策略差不多。

初始设\(\alpha=M^{\frac{n-1}2},\beta=M^{\frac{n+1}2}\)

只需要保证剩下的数\(\alpha,\beta\)满足\(Ans|(\alpha,\beta)\)即可。

同理将每个数\(x\),看作\(M^n/x\),然后将\(gcd,lcm\)反过来，可以保证\(M^n/\alpha|Ans\),同时\(M^n/\beta|Ans\)。也就是说\(Ans|\alpha,\beta\)。

策略可以抄A在偶数的时候的策略。