4.15 每日一题题解

Treepath

• 题目链接：https://ac.nowcoder.com/acm/problem/14248

涉及知识点：

• 树上dfs/dp

solution：

• \(以任意一个节点dfs（默认以1号节点dfs）\)
• \(因为树上任意两点之间的距离是固定的，所以我们可以dfs得到所有点距离1号节点的长度\)
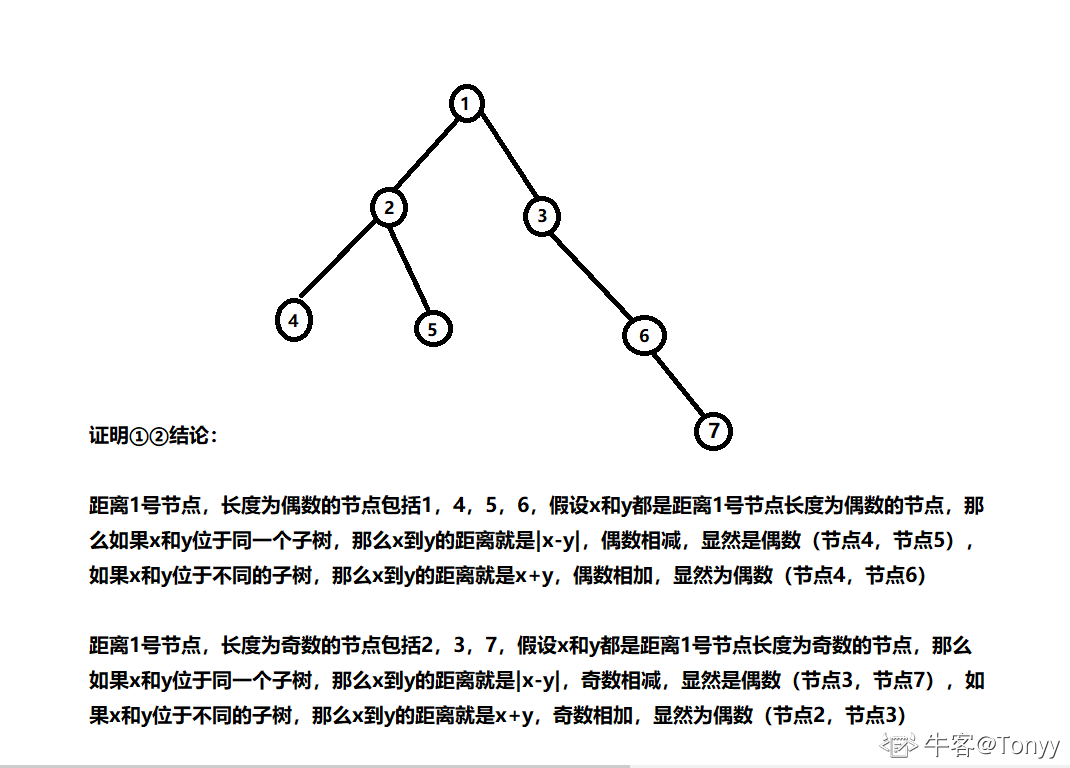
• \(存在两个结论（证明看下图）：\)
• \(①长度为偶数的任意两个节点之间的距离一定是偶数\)
• \(②长度为奇数的任意两个节点之间的距离也一定是偶数\)
• $最后记录距离1号节点长度为奇数的节点个数cnt1，距离1号节点长度为偶数的节点个数cnt2 $
• \(答案就是(cnt1*(cnt1-1)/2) + (cnt2*(cnt2-1)/2)\)
  

std:

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn = 1e5 + 5;
struct node{
  int t,nex;
};
node a[maxn<<1];
int head[maxn],tot,cnt[maxn];
void add(int x,int y){
    a[++tot].t = y,a[tot].nex = head[x],head[x] = tot;
}
void dfs(int x,int fa,int len)
{
    cnt[x] = len;
    for(int i=head[x]; i ; i=a[i].nex){
        if(a[i].t != fa)
            dfs(a[i].t , x , len + 1);
    }
}
int main()
{
    int n,x,y,cnt1 = 0 ,cnt2 = 0;
    cin>>n;
    for(int i=1;i<n;i++)
        cin>>x>>y,add(x,y),add(y,x);
    dfs(1 , 0 , 0);
    for(int i=1;i<=n;i++){
        if(cnt[i]%2)cnt1++;
        else cnt2++;
    }
    cout<<(1ll*cnt1*(cnt1 - 1)/2) + (1ll*cnt2*(cnt2 - 1)/2)<<endl;
    return 0;
}