Splay伸展树入门(单点操作,区间维护)附例题模板
Pps:终于学会了伸展树的区间操作,做一个完整的总结,总结一下自己的伸展树的单点操作和区间维护,顺便给未来的自己总结复习用。
splay是一种平衡树,【平均】操作复杂度O(nlogn)。首先平衡树先是一颗二叉搜索树,刚刚开始学的时候找题hash数字的题先测板子。。。
后来那题被学长改了数据不能用平衡树测了。。。一道二分数字的题。
二叉搜索树的功能是,插入一个数字,在O(logn)的时间内找到它,并操作,插入删除等。但是可能会让二叉搜索树退化成链,复杂度达到O(n)
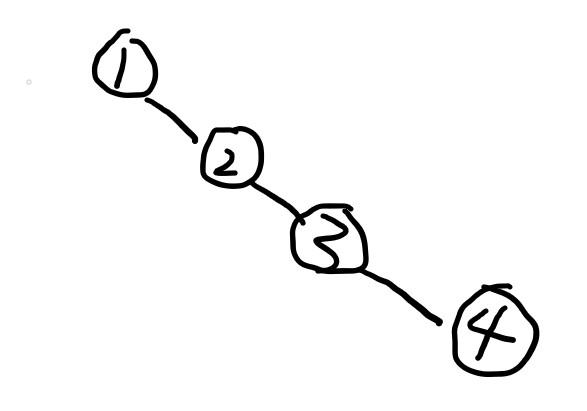
而平衡树就是通过一系列操作改变树的形态保存,尽可能把树的高度保持在logn,上图显然存在等价的树它不是一条链,
treap, avl, 红黑树,splay,替罪羊树。。。的各种巨巨发明的平衡方法,我选择了学splay,直接原因几个学长都用splay
而且splay相对红黑树等好写,能在ACM比赛的有限时间中改出来,而且能像线段树一样维护区间信息。
Splay不是严格平衡的,它是通过对每次操作的结点,操作后让它通过一系列旋转(zig, zag),伸展(splay)到根。80%的操作发生在20%的数据上,我们只要让它到根,尽快的取到就可以了。虽然它还是会退化成链,但是tarjan证明过它的均摊复杂度是O(nlogn)的。
我们先实现二叉搜索树的功能,存一个数字,判断它是否存在。
那么其实我们只要在插入数字,和查找数字后把那个结点旋转到根就满足了上面的要求。
先懂思路,大概文字能看的懂就好,代码实现可以慢慢继续往下看
其实旋转是无脑的。分为两种,右旋(zig),左旋(zag)。比如把x是它父节点的左儿子,那么它要往上走就要zig。反之就要zag
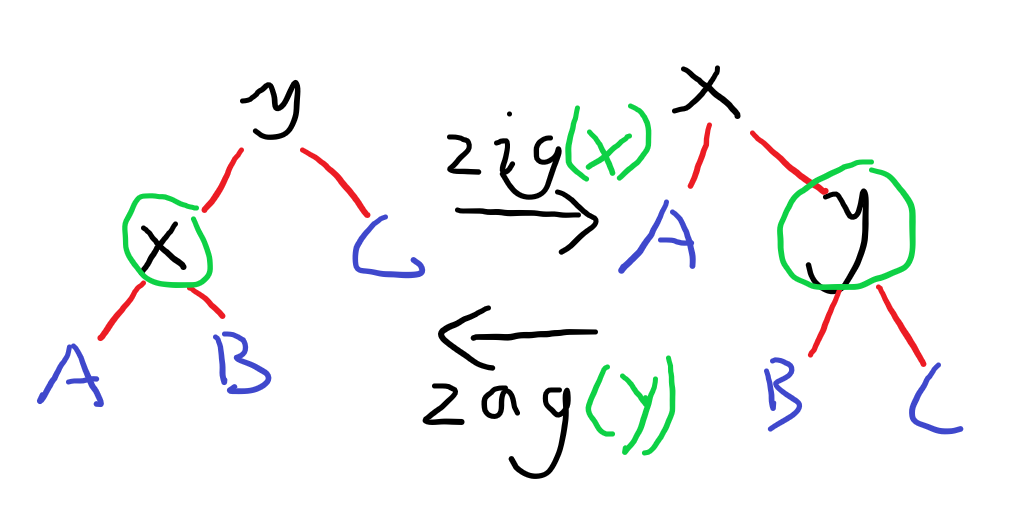
其中,x,y是节点,A,B,C可能是子树,也可以是空。左边到右边,旋转x,它是y的左儿子,就右旋转。右边到左边,y是x的右儿子就要左旋。
旋转方向的判断就判断是它父亲的左儿子还是右儿子即可。

仅仅上面的旋转是不够,Splay是需要双旋操作的。仅仅单旋的复杂度是O(n)的。
1,如果要旋转的结点x的父结点是根,那么只需要单旋。否则需要双旋转。
2,如果x和它的父节点y,同属于一种类型。这里的类型是指它们都是它父节点的右儿子,或者都是它父节点的左儿子。要先旋转y,再旋转x。
简单的解释就这样。复杂的细分就是其他巨巨博客说的zig-zig, zag-zag, zig - zag, zag-zig
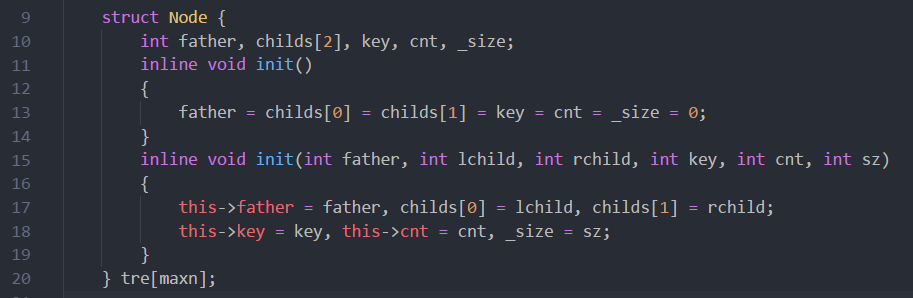
静态splay,key是关键字,那里判断大小的值,cnt是key出现的次数。比如你插入两个3,只要cnt++就好了,不用插入两个值为3的结点。
father表示这个结点的父结点是谁,childs[2]表示它儿子结点是谁,_size表示这个结点的子树总共有多少结点。
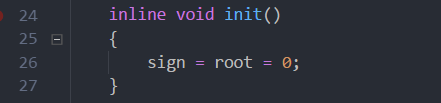
静态链表建的树,root表示整颗splay的根,0一直是不用的根。sign表示我们用的空间从结构体sign+1取,而不用new出来。
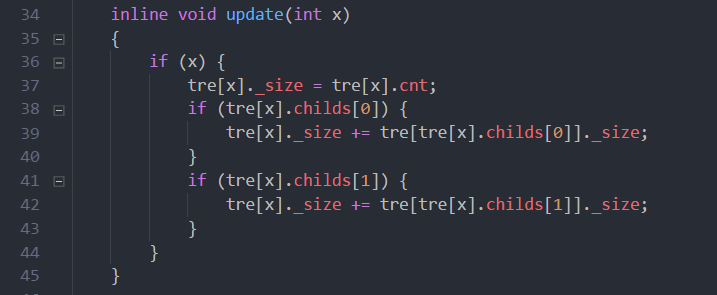
重新设置结点x的结点大小,主要是在旋转,伸展的过程中需要一路update上去。
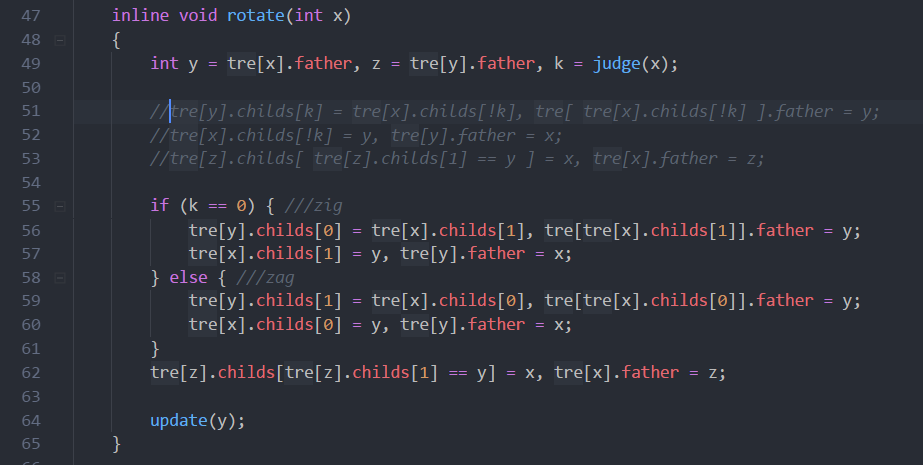
然后我的旋转函数,zig和zag可以合并。我注释那部分。像我这样比较菜的只会zig,zag分开写的顺一点。。。
我们用变量把x, y, z全记住,然后改指针就好了。拿zig为例。
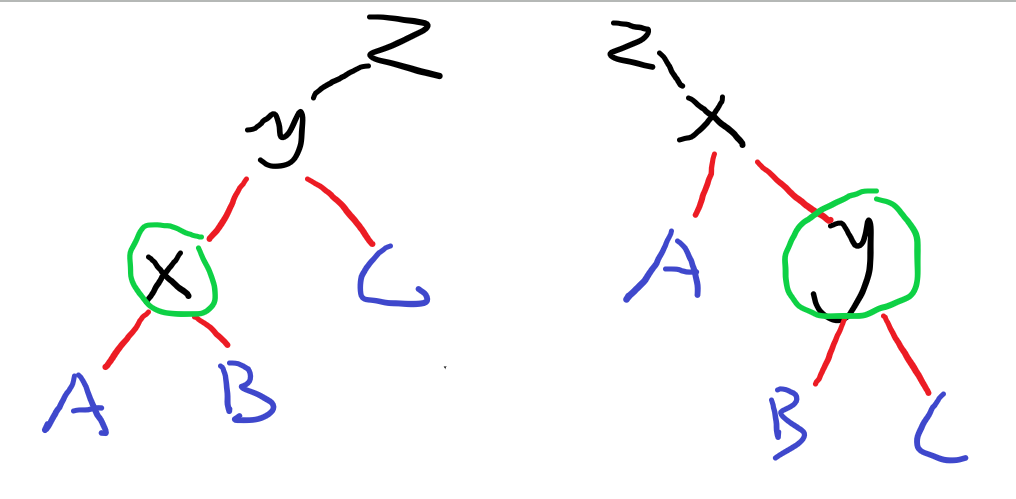
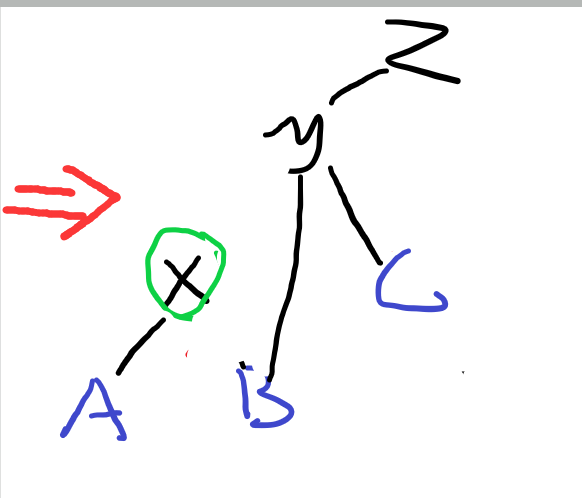
第一行改变了x与B的关系。
![]()

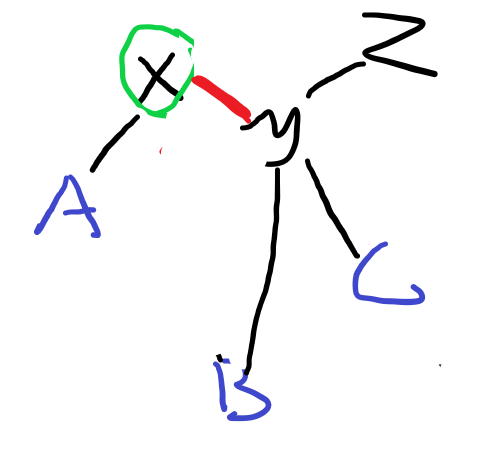
第二行是x, y的关系,下图红线
![]()
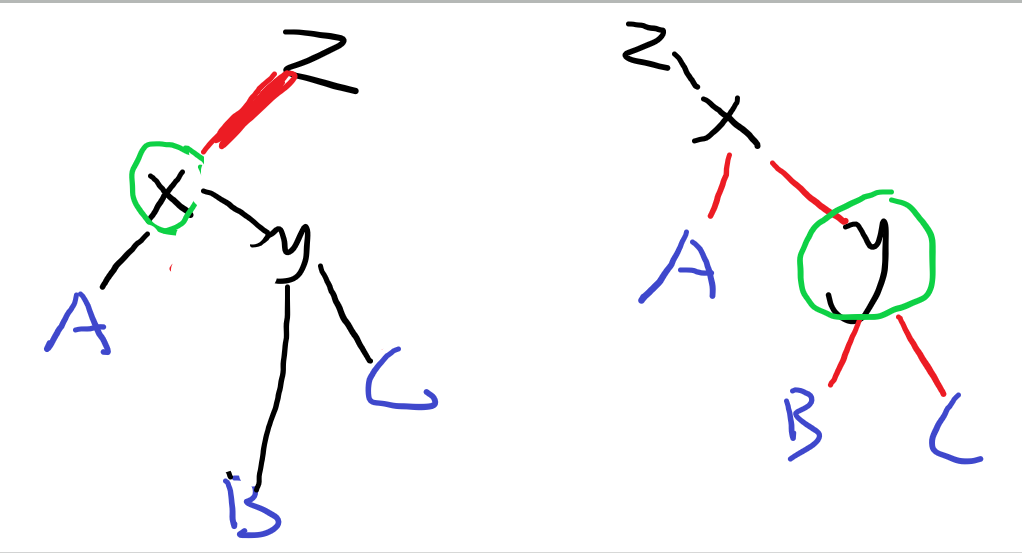
接下来如果z存在。把x, z的关系改好。就完成了一次旋转rotate ,就和最终的右图一样了。具体x是z的左儿子还是右儿子要判断。
![]()
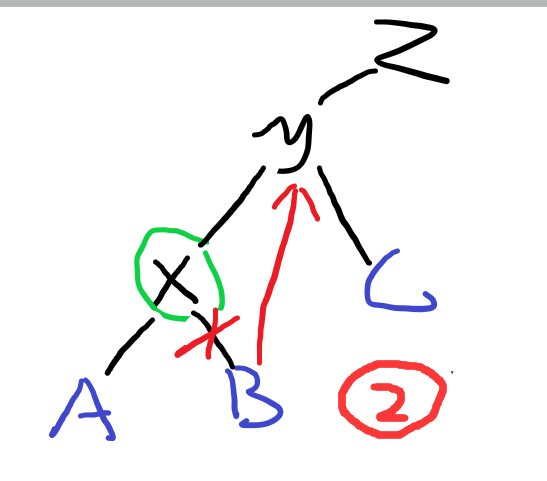
另外,可以注意到。rotate函数中我只update了y结点。理论上我改变了这么多结点,需要update的应该不止呀。这里其实是因为旋转完y是最低的结点。其他结点还需要继续splay。既然还需要改变,就不需要现在就急着splay。
把x结点旋转,goal是旋转后x的父节点。如果splay(x, 0)就是把x旋转到根。后面区间操作部分才需要修改goal.
if(goal == 0) root = x; 也是判断x是否旋转到根,没有旋转到根,根结点就不需要改变。在单点操作中if可以不需要直接root=x,但是区间操作中必须有。
然后我们插入数据。
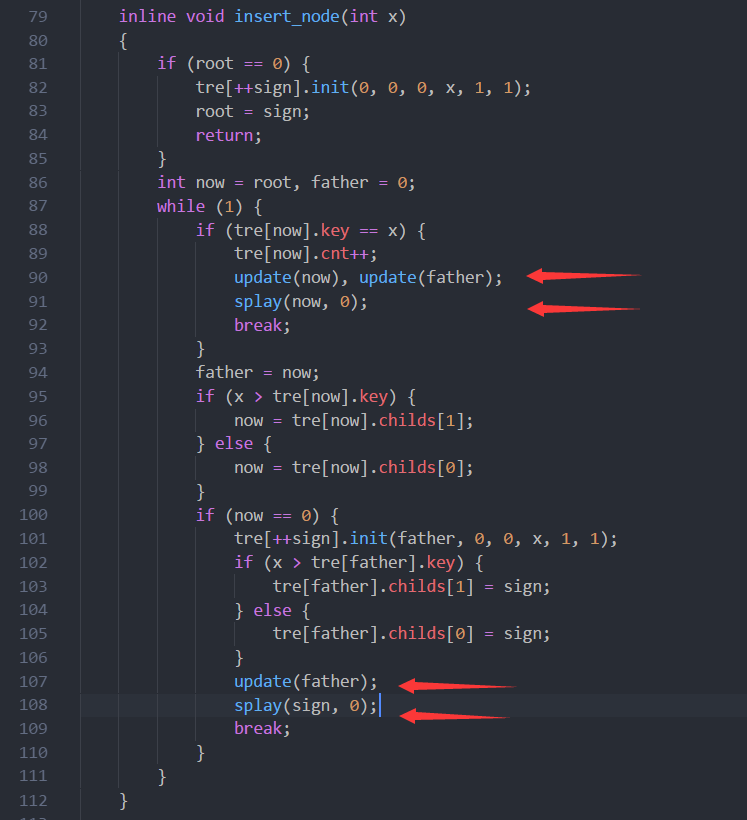
然后插入一个权值为x的数字。就是普通二叉排序树的插入。注意在找到结点和没找到结点创建节点后。把该节点splay到根。
init函数请参考上文的结构体。
然后解决些问题,找根节点的前驱后继。小于根节点最大的数,和大于根节点最小的数。
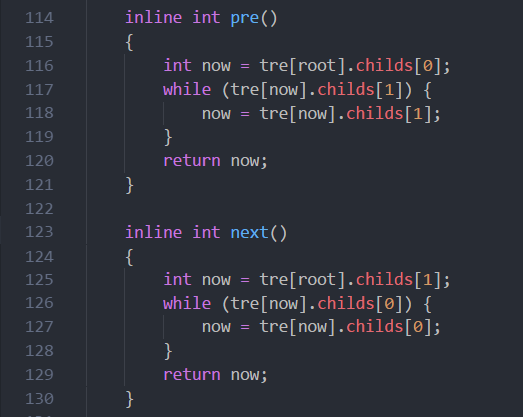
找key为x的节点的排名
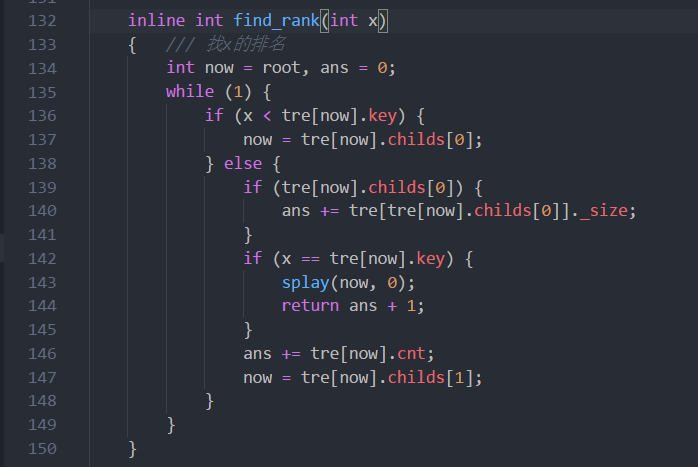
找排名为x的数
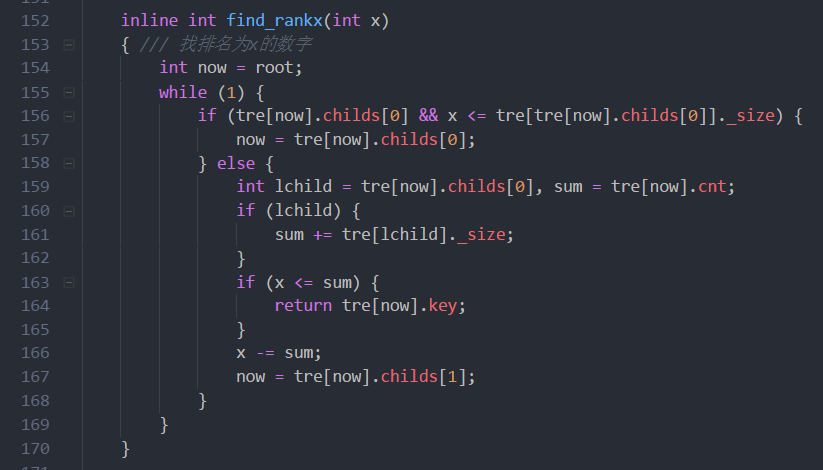
上面几个函数应该挺好看懂的,然后还有一个删除操作。splay的删除比较简单。他的思想是把待删除节点splay到root,删除根节点成为两颗子树,所以splay tree也有人叫分裂树。在把待删除旋转到根以后。
1,如果根节点的cnt>1,我们cnt--就结束了。
2,否则,原来的根节点必然是要丢掉的。在此条件下
1,如果左右子树都是空,那么整颗树也就空了,直接重置一颗空树。
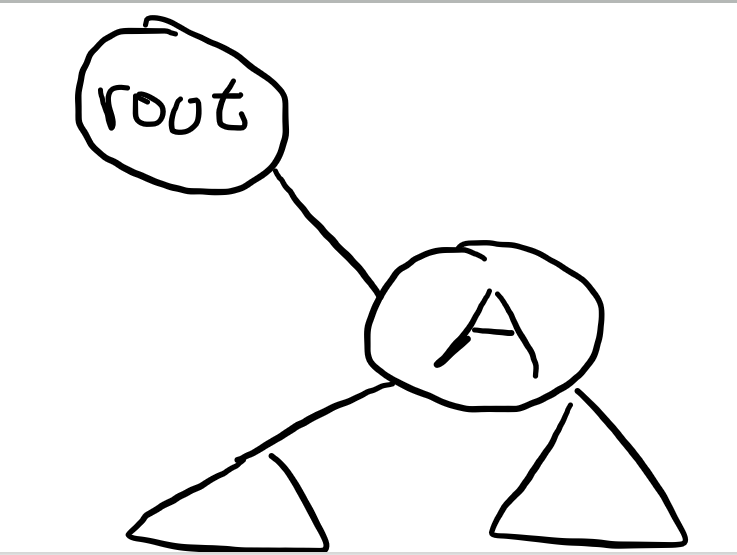
2,左子树,或右子树右一个是空。如图,我们只要把root指向A, 原来的root丢掉,把A的father=0;
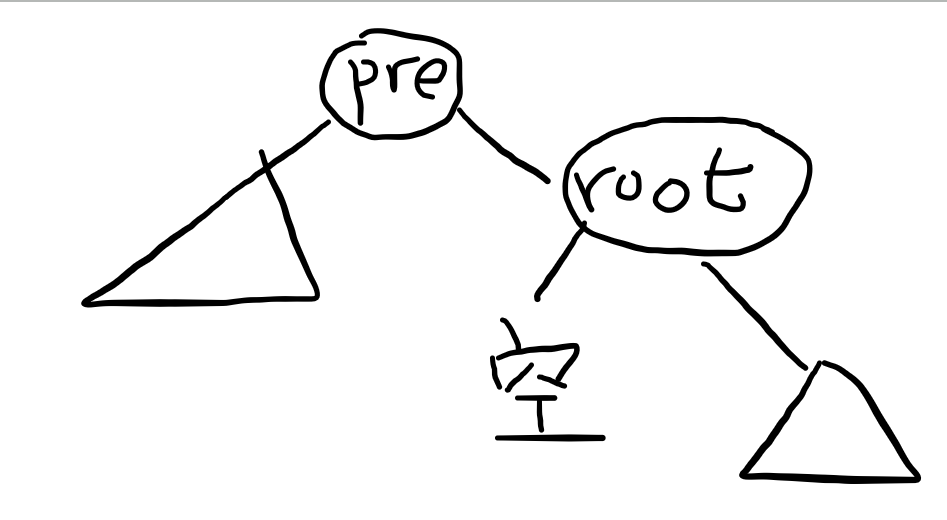
3,如果左右子树都存在。我们需要把root的前继旋转到根。因为是前继,所有结果会变成下图那样。root的左子树一点是空的。那么我们直接改变pre与root的右儿子的关系就好了。
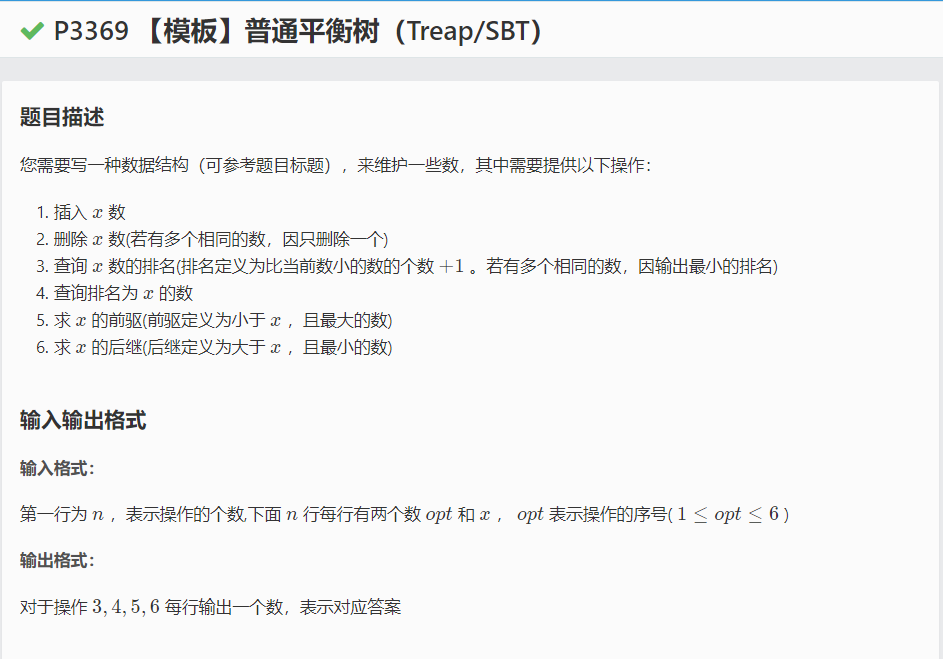
例题:洛谷P3369 https://www.luogu.org/problemnew/show/P3369
参考代码:

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 typedef long long LL; 5 const int maxn = 5e5 + 7; 6 7 struct Splay_Tree { 8 9 struct Node { 10 int father, childs[2], key, cnt, _size; 11 inline void init() { 12 father = childs[0] = childs[1] = key = cnt = _size = 0; 13 } 14 inline void init(int father, int lchild, int rchild, int key, int cnt, int sz) { 15 this -> father = father, childs[0] = lchild, childs[1] = rchild; 16 this -> key = key, this -> cnt = cnt, _size = sz; 17 } 18 } tre[maxn]; 19 int sign, root; 20 21 inline void init() { 22 sign = root = 0; 23 } 24 25 inline bool judge(int x) { 26 return tre[ tre[x].father ].childs[1] == x; 27 } 28 29 inline void update(int x) { 30 if(x) { 31 tre[x]._size = tre[x].cnt; 32 if(tre[x].childs[0]) { 33 tre[x]._size += tre[ tre[x].childs[0] ]._size; 34 } 35 if(tre[x].childs[1]) { 36 tre[x]._size += tre[ tre[x].childs[1] ]._size; 37 } 38 } 39 } 40 41 inline void rotate(int x) { 42 int y = tre[x].father, z = tre[y].father, k = judge(x); 43 44 //tre[y].childs[k] = tre[x].childs[!k], tre[ tre[x].childs[!k] ].father = y; 45 //tre[x].childs[!k] = y, tre[y].father = x; 46 //tre[z].childs[ tre[z].childs[1] == y ] = x, tre[x].father = z; 47 48 if(k == 0) { ///zig 49 tre[y].childs[0] = tre[x].childs[1], tre[ tre[x].childs[1] ].father = y; 50 tre[x].childs[1] = y, tre[y].father = x; 51 } else { ///zag 52 tre[y].childs[1] = tre[x].childs[0], tre[ tre[x].childs[0] ].father = y; 53 tre[x].childs[0] = y, tre[y].father = x; 54 } 55 tre[z].childs[ tre[z].childs[1] == y ] = x, tre[x].father = z; 56 57 update(y); 58 } 59 60 inline void splay(int x,int goal) { 61 for(int father; (father = tre[x].father) != goal; rotate(x) ) { 62 if(tre[father].father != goal) { 63 rotate(judge(x) == judge(father) ? father : x); 64 } 65 } 66 root = x; 67 } 68 69 inline void insert_node(int x) { 70 if(root == 0) { 71 tre[++sign].init(0, 0, 0, x, 1, 1); 72 root = sign; 73 return ; 74 } 75 int now = root, father = 0; 76 while(1) { 77 if(tre[now].key == x) { 78 tre[now].cnt ++; 79 update(now), update(father); 80 splay(now, 0); 81 break; 82 } 83 father = now; 84 if(x > tre[now].key) { 85 now = tre[now].childs[1]; 86 } else { 87 now = tre[now].childs[0]; 88 } 89 if(now == 0) { 90 tre[++sign].init(father, 0, 0, x, 1, 1); 91 if(x > tre[father].key) { 92 tre[father].childs[1] = sign; 93 } else { 94 tre[father].childs[0] = sign; 95 } 96 update(father); 97 splay(sign, 0); 98 break; 99 } 100 } 101 } 102 103 inline int pre() { 104 int now = tre[root].childs[0]; 105 while(tre[now].childs[1]) { 106 now = tre[now].childs[1]; 107 } 108 return now; 109 } 110 111 inline int next() { 112 int now = tre[root].childs[1]; 113 while(tre[now].childs[0]) { 114 now = tre[now].childs[0]; 115 } 116 return now; 117 } 118 119 inline int find_rank(int x) { /// 找x的排名 120 int now = root, ans = 0; 121 while(1) { 122 if(x < tre[now].key) { 123 now = tre[now].childs[0]; 124 } 125 else { 126 if(tre[now].childs[0]) { 127 ans += tre[ tre[now].childs[0] ]._size; 128 } 129 if(x == tre[now].key) { 130 splay(now, 0); 131 return ans + 1; 132 } 133 ans += tre[now].cnt; 134 now = tre[now].childs[1]; 135 } 136 } 137 } 138 139 inline int find_rankx(int x) { /// 找排名为x的数字 140 int now = root; 141 while(1) { 142 if(tre[now].childs[0] && x <= tre[ tre[now].childs[0] ]._size ) { 143 now = tre[now].childs[0]; 144 } else { 145 int lchild = tre[now].childs[0], sum = tre[now].cnt; 146 if(lchild) { 147 sum += tre[lchild]._size; 148 } 149 if(x <= sum) { 150 return tre[now].key; 151 } 152 x -= sum; 153 now = tre[now].childs[1]; 154 } 155 } 156 } 157 158 inline void del(int x) { 159 find_rank(x); 160 if(tre[root].cnt > 1) { 161 tre[root].cnt --; 162 update(root); 163 return ; 164 } 165 if(!tre[root].childs[0] && !tre[root].childs[1]) { 166 tre[root].init(); 167 root = 0; 168 return ; 169 } 170 if(!tre[root].childs[0]) { 171 int old_root = root; 172 root = tre[root].childs[1], tre[root].father = 0, tre[old_root].init(); 173 return ; 174 } 175 if(!tre[root].childs[1]) { 176 int old_root = root; 177 root = tre[root].childs[0], tre[root].father = 0, tre[old_root].init(); 178 return ; 179 } 180 int pre_node = pre(), old_root = root; 181 splay(pre_node, 0); 182 tre[root].childs[1] = tre[old_root].childs[1]; 183 tre[ tre[old_root].childs[1] ].father = root; 184 tre[old_root].init(); 185 update(root); 186 } 187 188 inline bool find(int x) { 189 int now = root; 190 while(1) { 191 if(now == 0) { 192 return 0; 193 } 194 if(x == tre[now].key) { 195 splay(now, 0); 196 return 1; 197 } 198 if(x > tre[now].key) { 199 now = tre[now].childs[1]; 200 } else { 201 now = tre[now].childs[0]; 202 } 203 } 204 } 205 206 } S; 207 208 int n, opt, x; 209 210 int main() { 211 while(~scanf("%d",&n)) { 212 S.init(); 213 for(int i = 1; i <= n; i ++ ) { 214 scanf("%d %d",&opt, &x); 215 switch(opt) { 216 case 1: 217 S.insert_node(x); 218 break; 219 case 2: 220 S.del(x); 221 break; 222 case 3: 223 printf("%d\n",S.find_rank(x)); 224 break; 225 case 4: 226 printf("%d\n",S.find_rankx(x)); 227 break; 228 case 5: 229 S.insert_node(x); 230 printf("%d\n",S.tre[S.pre()].key); 231 S.del(x); 232 break; 233 case 6: 234 S.insert_node(x); 235 printf("%d\n",S.tre[S.next()].key); 236 S.del(x); 237 break; 238 } 239 } 240 } 241 return 0; 242 }
splay的区间维护。
我们可以把下标作为key,插入平衡树。把L-1旋转到根,R+1旋转到根的右子树。根据平衡树的性质一点是这样的。这样区间[L,R]就到了根的右子树的左子树了。如图。
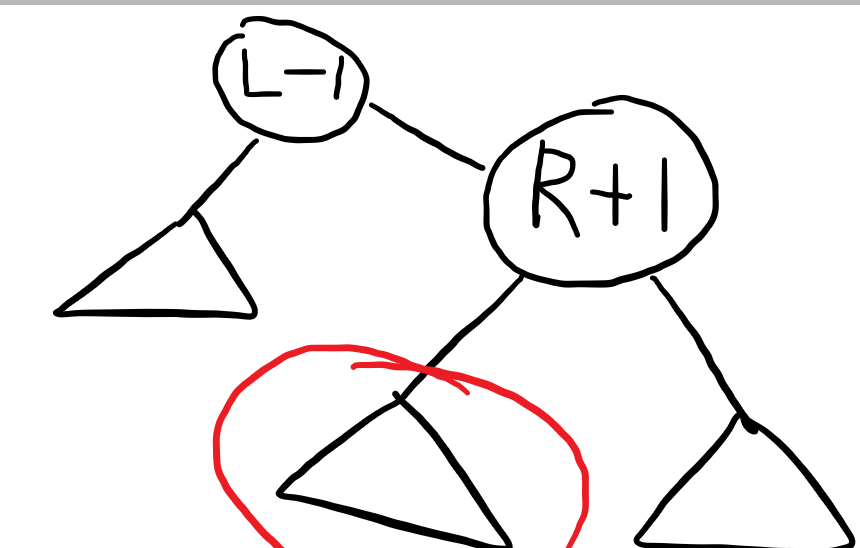
这样我们对区间的操作都可以写在节点上,还可以直接给节点打lazy标记。
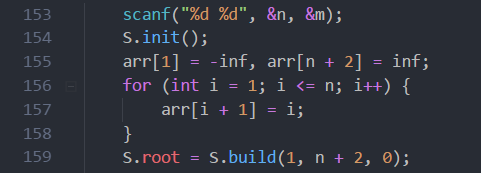
我们需要给数组的n个元素开头来个-inf, 末尾来个inf,保持树的结构,然后类似线段树那样递归建树,直接就是平衡的。比较懒的一个一个insert也可以。
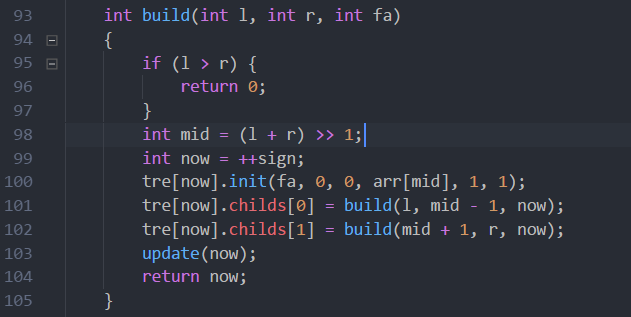
然后就是上面说的旋转L-1,R+1区间,然后给节点打标记了。
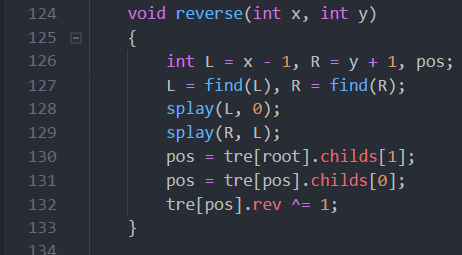
然后就是pushdown了,这部分初学的时候,我懵逼在了这里,尤其是为什么要swap左右节点的指针。貌似会改变平衡树的有序性。这里要自己想一想。
网上竟然没有一份代码解释了这里囧。。。
个人理解:首先我们找L,R的时候通过的是节点的size(详情看我的find函数),而不是直接找key为L的值,而key的cnt也就是节点位置重复元素都是1。我们确实不需要右儿子的key大于节点,左儿子的key小于这个性质。而我们在旋转L-1,R+1的节点后,[L,R]区间又体现为一个节点。每次都是同一个。
这里的pushdown只是延迟标记,我们要证明swap的正确性只要证明swap到底的正确性即可。
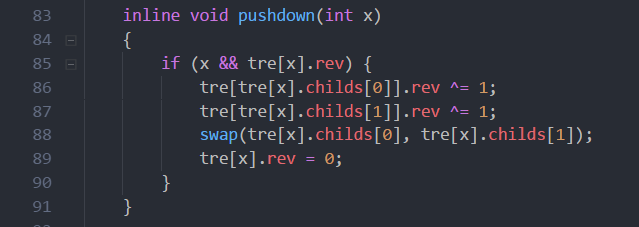
例题:洛谷P3391 只有区间翻转的例题 https://www.luogu.org/problemnew/show/P3391
参考代码:

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 typedef long long LL; 5 const int maxn = 5e5 + 7; 6 const int inf = 1e9 + 7; 7 8 int n, m, arr[maxn]; 9 10 struct Splay_Tree { 11 12 struct Node { 13 int father, childs[2], key, cnt, _size, rev; 14 inline void init() { 15 father = childs[0] = childs[1] = key = cnt = _size = rev = 0; 16 } 17 inline void init(int father, int lchild, int rchild, int key, int cnt, int sz) { 18 this -> father = father, childs[0] = lchild, childs[1] = rchild; 19 this -> key = key, this -> cnt = cnt, _size = sz; 20 this -> rev = 0; 21 } 22 } tre[maxn]; 23 int sign, root; 24 25 inline void init() { 26 sign = root = 0; 27 } 28 29 inline bool judge(int x) { 30 return tre[ tre[x].father ].childs[1] == x; 31 } 32 33 inline void update(int x) { 34 if(x) { 35 tre[x]._size = tre[x].cnt; 36 if(tre[x].childs[0]) { 37 tre[x]._size += tre[ tre[x].childs[0] ]._size; 38 } 39 if(tre[x].childs[1]) { 40 tre[x]._size += tre[ tre[x].childs[1] ]._size; 41 } 42 } 43 } 44 45 inline void rotate(int x) { 46 47 int y = tre[x].father, z = tre[y].father, k = judge(x); 48 pushdown(y), pushdown(x); 49 //tre[y].childs[k] = tre[x].childs[!k], tre[ tre[x].childs[!k] ].father = y; 50 //tre[x].childs[!k] = y, tre[y].father = x; 51 //tre[z].childs[ tre[z].childs[1] == y ] = x, tre[x].father = z; 52 if(k == 0) {///zig 53 tre[y].childs[0] = tre[x].childs[1], tre[ tre[x].childs[1] ].father = y; 54 tre[x].childs[1] = y, tre[y].father = x; 55 } else { ///zag 56 tre[y].childs[1] = tre[x].childs[0], tre[ tre[x].childs[0] ].father = y; 57 tre[x].childs[0] = y, tre[y].father = x; 58 } 59 tre[z].childs[ tre[z].childs[1] == y ] = x, tre[x].father = z; 60 61 update(y); 62 63 } 64 65 inline void splay(int x,int goal) { 66 for(int father; (father = tre[x].father) != goal; rotate(x) ) { 67 if(tre[father].father != goal) { 68 rotate(judge(x) == judge(father) ? father : x); 69 } 70 } 71 if(goal == 0) { root = x; } 72 } 73 74 inline void pushdown(int x) { 75 if(x && tre[x].rev) { 76 tre[ tre[x].childs[0] ].rev ^= 1; 77 tre[ tre[x].childs[1] ].rev ^= 1; 78 swap(tre[x].childs[0], tre[x].childs[1]); 79 tre[x].rev = 0; 80 } 81 } 82 83 int build(int l, int r, int fa) { 84 if(l > r) { return 0; } 85 int mid = (l + r) >> 1; 86 /* 87 tre[++sign].init(fa, 0, 0, arr[mid], 1, 1); 88 tre[sign].childs[0] = build(l, mid - 1, sign); 89 tre[sign].childs[1] = build(mid + 1, r, sign); 90 update(sign); 91 return sign; 92 */ 93 ///now是必须的,sign在递归build的过程中变化了,上面就是死循环的例子 94 int now = ++ sign; 95 tre[now].init(fa, 0, 0, arr[mid], 1, 1); 96 tre[now].childs[0] = build(l, mid - 1, now); 97 tre[now].childs[1] = build(mid + 1, r, now); 98 update(now); 99 return now; 100 } 101 102 int find(int x) { 103 int now = root; 104 while(1) { 105 pushdown(now); 106 if(x <= tre[ tre[now].childs[0] ]._size) { 107 now = tre[now].childs[0]; 108 } else { 109 x -= tre[ tre[now].childs[0] ]._size + 1; 110 if(!x) { 111 return now; 112 } 113 now = tre[now].childs[1]; 114 } 115 } 116 } 117 118 void reverse(int x, int y) { 119 int L = x - 1, R = y + 1, pos; 120 L = find(L), R = find(R); 121 splay(L, 0); 122 splay(R, L); 123 pos = tre[root].childs[1]; 124 pos = tre[pos].childs[0]; 125 tre[pos].rev ^= 1; 126 } 127 128 inline void dfs(int now) { 129 pushdown(now); 130 if(tre[now].childs[0]) { dfs(tre[now].childs[0]); } 131 if(tre[now].key != -inf && tre[now].key != inf) { 132 printf("%d ", tre[now].key); 133 } 134 if(tre[now].childs[1]) { dfs(tre[now].childs[1]); } 135 } 136 137 } S; 138 139 int main() 140 { 141 scanf("%d %d", &n, &m); 142 S.init(); 143 arr[1] = -inf, arr[n + 2] = inf; 144 for(int i = 1; i <= n; i ++ ) { 145 arr[i + 1] = i; 146 } 147 S.root = S.build(1, n + 2, 0); 148 for(int i = 1; i <= m; i ++ ) { 149 int x, y; 150 scanf("%d %d", &x, &y); 151 S.reverse(x + 1, y + 1); 152 } 153 S.dfs(S.root); 154 return 0; 155 }


