决策树之ID3算法

文章目录

• 预备知识
• • 信息熵(information entropy)
  • 条件熵
  • 信息增益(information gain)
  • 递归返回条件
• ID3算法
• 代码实现
• • 绘图结果
• 参考博客

预备知识

信息熵(information entropy)

一句话概括：信息熵用来度量信息的不确定性，或者说用来度量样本集合的纯度，信息熵越小则信息的不确定性越低，样本集合纯度越高。生成决策树的过程就是不确定度降低的过程，或者说就是样本纯度提高的过程。
公式：假设样本集合为D，样本集合中有k类样本（$k=1,2,...|y|$），$p_k$代表第k类样本在样本集合D中的比例，则信息熵定义为：
$$Ent(D)=-\sum _{k=1}^{|y|}{p}_{k}lo{g}_2{p}_k(1)$$

---

条件熵

一句话概括:已知某个属性a,其有V个可能取值{$a^1,a^2,...,a^V$},每个取值$a^{\ast }$将样本集合D划分为V个子集{$D^1,D^2,...,D^V$},分别对这V个子集求信息熵并赋予权重$\frac{|D^v|}{|D|}$再求和,权重越大即样本数越多，代表分支节点的影响越大。条件熵定义如下:
$$Ent(D,a)=\sum _{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)(2)$$

---

信息增益(information gain)

一句话概括:信息增益越大，则按某属性a对样本集合D划分后，子集(子节点)较父集的样本纯度提升的越高,或者说不确定性降低的越多。其定义为：样本集合D的信息熵减去按某属性a划分后的条件熵。
$$Gain(D,a)=Ent(D)-\sum _{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)(3)$$

---

递归返回条件

• 节点中包含的样本全部属于同一个类别C，则无需划分

• 当属性集为空，或 所有样本在所有属性上取值一样则无法划分

• 当前节点的样本集合为空，则不能划分

---

ID3算法

ID3算法就是以信息增益来选择划分属性。举一个例子，下面是一个西瓜数据集，用来学习一棵是不是好瓜的决策树，显然$|y|=2$（$C_1=是,C_2=否$）

编号	色泽	根蒂	敲声	纹理	脐部	触感	好瓜
1	青绿	蜷缩	浊响	清晰	凹陷	硬滑	是
2	乌黑	蜷缩	沉闷	清晰	凹陷	硬滑	是
3	乌黑	蜷缩	浊响	清晰	凹陷	硬滑	是
4	青绿	蜷缩	沉闷	清晰	凹陷	硬滑	是
5	浅白	蜷缩	浊响	清晰	凹陷	硬滑	是
6	青绿	稍蜷	浊响	清晰	稍凹	软粘	是
7	乌黑	稍蜷	浊响	稍糊	稍凹	软粘	是
8	乌黑	稍蜷	浊响	清晰	稍凹	硬滑	是
9	乌黑	稍蜷	沉闷	稍糊	稍凹	硬滑	否
10	青绿	硬挺	清脆	清晰	平坦	软粘	否
11	浅白	硬挺	清脆	模糊	平坦	硬滑	否
12	浅白	蜷缩	浊响	模糊	平坦	软粘	否
13	青绿	稍蜷	浊响	稍糊	凹陷	硬滑	否
14	浅白	稍蜷	沉闷	稍糊	凹陷	硬滑	否
15	乌黑	稍蜷	浊响	清晰	稍凹	软粘	否
16	浅白	蜷缩	浊响	模糊	平坦	硬滑	否
17	青绿	蜷缩	沉闷	稍糊	稍凹	硬滑	否

• 首先确定以哪个属性作为根节点
  step1:
  根节点包含样本集合D中的所有样例，其中正例$p_1$占$\frac{8}{17}$，反例$p_2$占$\frac{9}{17}$，代入公式(1)计算信息熵:
  $$Ent(D)=-\sum _{k=1}^{|y|}{p}_{k}lo{g}_2{p}_k=-(\frac{8}{17}lo{g}_2\frac{8}{17}+\frac{9}{17}lo{g}_2\frac{9}{17})=0.998$$
  step2:
  再以属性“色泽”为例，它有三个可能的取值{青绿,乌黑,浅白}，将样本集合D划分为了三个样本子集{$D^1,D^2,D^3$}，如下表所示,分别计算其信息熵。

---

$$D^1$$

编号	色泽	根蒂	敲声	纹理	脐部	触感	好瓜
1	青绿	蜷缩	浊响	清晰	凹陷	硬滑	是
4	青绿	蜷缩	沉闷	清晰	凹陷	硬滑	是
6	青绿	稍蜷	浊响	清晰	稍凹	软粘	是
10	青绿	硬挺	清脆	清晰	平坦	软粘	否
13	青绿	稍蜷	浊响	稍糊	凹陷	硬滑	否
17	青绿	蜷缩	沉闷	稍糊	稍凹	硬滑	否

样本子集$D^1$样本数为6，$|y|=2$，正例$p_1$占$\frac{3}{6}$，反例$p_2$占$\frac{3}{6}$，代入公式(1)：

$$E(D^1)=-(\frac{3}{6}lo{g}_2\frac{3}{6}+\frac{3}{6}lo{g}_2\frac{3}{6})=1.000$$

---

$$D^2$$

编号	色泽	根蒂	敲声	纹理	脐部	触感	好瓜
2	乌黑	蜷缩	沉闷	清晰	凹陷	硬滑	是
3	乌黑	蜷缩	浊响	清晰	凹陷	硬滑	是
7	乌黑	稍蜷	浊响	稍糊	稍凹	软粘	是
8	乌黑	稍蜷	浊响	清晰	稍凹	硬滑	是
9	乌黑	稍蜷	沉闷	稍糊	稍凹	硬滑	否
15	乌黑	稍蜷	浊响	清晰	稍凹	软粘	否

样本子集$D^2$的样本数为6，$|y|=2$，正例$p_1$占$\frac{2}{3}$，反例$p_2$占$\frac{1}{3}$，代入公式(1)：
$$Ent(D^2)=-(\frac{2}{3}lo{g}_2\frac{2}{3}+\frac{1}{3}lo{g}_2\frac{1}{3})=0.918$$

---

$$D^3$$

编号	色泽	根蒂	敲声	纹理	脐部	触感	好瓜
5	浅白	蜷缩	浊响	清晰	凹陷	硬滑	是
11	浅白	硬挺	清脆	模糊	平坦	硬滑	否
12	浅白	蜷缩	浊响	模糊	平坦	软粘	否
14	浅白	稍蜷	沉闷	稍糊	凹陷	硬滑	否
16	浅白	蜷缩	浊响	模糊	平坦	硬滑	否

样本子集$D^3$的样本数为5，$|y|=2$，正例$p_1$占$\frac{1}{5}$，反例$p_2$占$\frac{4}{5}$，代入公式(1)：
$$Ent(D^3)=-(\frac{1}{5}lo{g}_2\frac{1}{5}+\frac{4}{5}lo{g}_2\frac{4}{5})=0.722$$

---

step3：
对$Ent(D^1)，Ent(D^2)，Ent(D^3)$分别赋予权重计算条件熵:
$子集D^1和D^2占样本集合D的\frac{6}{17},子集D^3占\frac{5}{17}$
$$Ent(D,色泽)=\frac{6}{17}\ast 1.000+\frac{6}{17}\ast 0.918+\frac{5}{17}\ast 0.722=0.889$$
step4:
计算通过"色泽"属性对样本集合$D$划分的信息增益:
$$Gain(D,色泽)=Ent(D)-Ent(D,色泽)=0.998-0.889=0.109$$
step5:
重复以上步骤计算按其余属性划分样本集合$D$的信息增益:
$$Gain(D,根蒂)=0.143$$$$Gain(D,敲声)=0.141$$$$Gain(D,纹理)=0.381$$$$Gain(D,脐部)=0.289$$$$Gain(D,触感)=0.006$$
step6：
将信息增益最大的属性作为划分属性，显然"纹理"属性信息增益最大，所以将"纹理"属性作为根节点。划分结果如图所示。

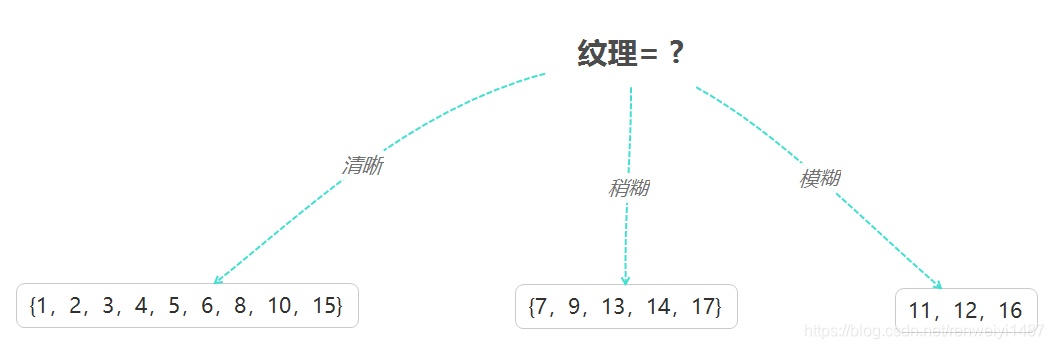
• 然后对每个分支节点做进一步的划分
  以第一个分支节点为例，样本集合$D^1$中有9个样例，可用属性集合为{色泽，根蒂，敲声，脐部，触感，好瓜}，由$D^1$计算各属性增益:

$$Gain(D^1,色泽)=0.043$$$$Gain(D^1,根蒂)=0.0485$$$$Gain(D^1,敲声)=0.331$$$$Gain(D^1,脐部)=0.458$$$$Gain(D^1,触感)=0.458$$
“根蒂”，“脐部”，“触感”三个属性信息增益均最大，可任选其一

• 对每个分支节点做以上操作最后得到完整的决策树:

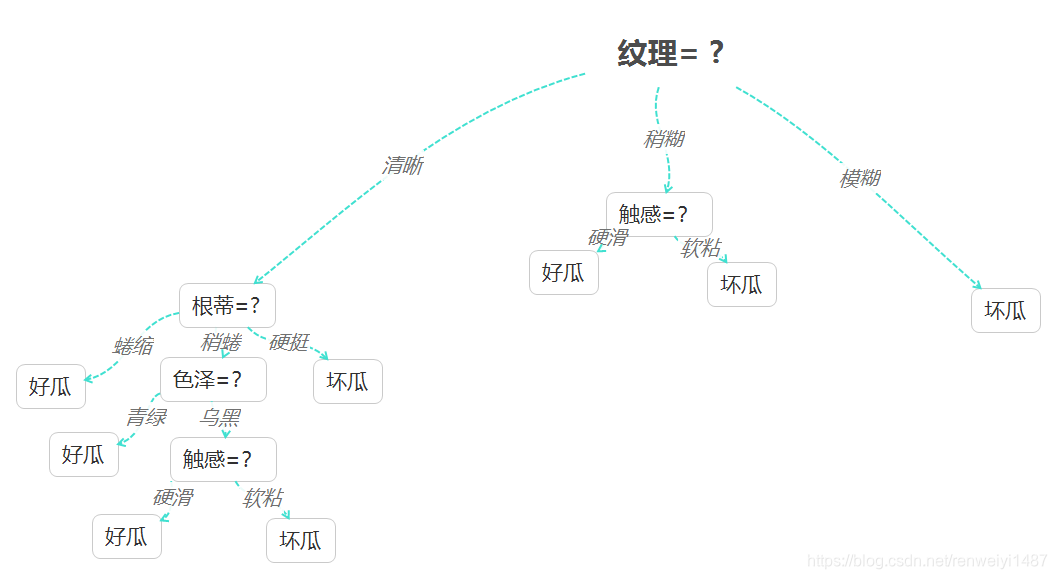
代码实现

# _*_ coding: UTF-8 _*_

import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['KaiTi']
mpl.rcParams['font.serif'] = ['KaiTi']

"""绘决策树的函数"""
decisionNode = dict(boxstyle="sawtooth", fc="0.8")  # 定义分支点的样式
leafNode = dict(boxstyle="round4", fc="0.8")  # 定义叶节点的样式
arrow_args = dict(arrowstyle="<-")  # 定义箭头标识样式


# 计算树的叶子节点数量
def getNumLeafs(myTree):
   numLeafs = 0
   firstStr = list(myTree.keys())[0]
   secondDict = myTree[firstStr]
   for key in secondDict.keys():
      if type(secondDict[key]).__name__ == 'dict':
         numLeafs += getNumLeafs(secondDict[key])
      else:
         numLeafs += 1
   return numLeafs


# 计算树的最大深度
def getTreeDepth(myTree):
   maxDepth = 0
   firstStr = list(myTree.keys())[0]
   secondDict = myTree[firstStr]
   for key in secondDict.keys():
      if type(secondDict[key]).__name__ == 'dict':
         thisDepth = 1 + getTreeDepth(secondDict[key])
      else:
         thisDepth = 1
      if thisDepth > maxDepth:
         maxDepth = thisDepth
   return maxDepth


# 画出节点
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
   createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', \
                           xytext=centerPt, textcoords='axes fraction', va="center", ha="center", \
                           bbox=nodeType, arrowprops=arrow_args)


# 标箭头上的文字
def plotMidText(cntrPt, parentPt, txtString):
   lens = len(txtString)
   xMid = (parentPt[0] + cntrPt[0]) / 2.0 - lens * 0.002
   yMid = (parentPt[1] + cntrPt[1]) / 2.0
   createPlot.ax1.text(xMid, yMid, txtString)


def plotTree(myTree, parentPt, nodeTxt):
   numLeafs = getNumLeafs(myTree)
   depth = getTreeDepth(myTree)
   firstStr = list(myTree.keys())[0]
   cntrPt = (plotTree.x0ff + \
             (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.y0ff)
   plotMidText(cntrPt, parentPt, nodeTxt)
   plotNode(firstStr, cntrPt, parentPt, decisionNode)
   secondDict = myTree[firstStr]
   plotTree.y0ff = plotTree.y0ff - 1.0 / plotTree.totalD
   for key in secondDict.keys():
      if type(secondDict[key]).__name__ == 'dict':
         plotTree(secondDict[key], cntrPt, str(key))
      else:
         plotTree.x0ff = plotTree.x0ff + 1.0 / plotTree.totalW
         plotNode(secondDict[key], \
                  (plotTree.x0ff, plotTree.y0ff), cntrPt, leafNode)
         plotMidText((plotTree.x0ff, plotTree.y0ff) \
                     , cntrPt, str(key))
   plotTree.y0ff = plotTree.y0ff + 1.0 / plotTree.totalD


def createPlot(inTree):
   fig = plt.figure(1, facecolor='white')
   fig.clf()
   axprops = dict(xticks=[], yticks=[])
   createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
   plotTree.totalW = float(getNumLeafs(inTree))
   plotTree.totalD = float(getTreeDepth(inTree))
   plotTree.x0ff = -0.5 / plotTree.totalW
   plotTree.y0ff = 1.0
   plotTree(inTree, (0.5, 1.0), '')
   plt.show()

if __name__=='__main__':
    createPlot()

from math import log
import operator
import treePlotter

dataSet = [['青绿'	,'蜷缩'	,'浊响'	,'清晰'	,'凹陷'	,'硬滑'	,'好瓜'],
           ['乌黑'	,'蜷缩'	,'沉闷'	,'清晰'	,'凹陷'	,'硬滑'	,'好瓜'],
           ['乌黑'	,'蜷缩'	,'浊响'	,'清晰'	,'凹陷'	,'硬滑'	,'好瓜'],
           ['青绿'	,'蜷缩'	,'沉闷'	,'清晰'	,'凹陷'	,'硬滑'	,'好瓜'],
           ['浅白'	,'蜷缩'	,'浊响'	,'清晰'	,'凹陷'	,'硬滑'	,'好瓜'],
           ['青绿'	,'稍蜷'	,'浊响'	,'清晰'	,'稍凹'	,'软粘'	,'好瓜'],
           ['乌黑'	,'稍蜷'	,'浊响'	,'稍糊'	,'稍凹'	,'软粘'	,'好瓜'],
           ['乌黑'	,'稍蜷'	,'浊响'	,'清晰'	,'稍凹'	,'硬滑'	,'好瓜'],
           ['乌黑'	,'稍蜷'	,'沉闷'	,'稍糊'	,'稍凹'	,'硬滑'	,'坏瓜'],
           ['青绿'	,'硬挺'	,'清脆'	,'清晰'	,'平坦'	,'软粘'	,'坏瓜'],
           ['浅白'	,'硬挺'	,'清脆'	,'模糊'	,'平坦'	,'硬滑'	,'坏瓜'],
           ['浅白'	,'蜷缩'	,'浊响'	,'模糊'	,'平坦'	,'软粘'	,'坏瓜'],
           ['青绿'	,'稍蜷'	,'浊响'	,'稍糊'	,'凹陷'	,'硬滑'	,'坏瓜'],
           ['浅白'	,'稍蜷'	,'沉闷'	,'稍糊'	,'凹陷'	,'硬滑'	,'坏瓜'],
           ['乌黑'	,'稍蜷'	,'浊响'	,'清晰'	,'稍凹'	,'软粘'	,'坏瓜'],
           ['浅白'	,'蜷缩'	,'浊响'	,'模糊'	,'平坦'	,'硬滑'	,'坏瓜'],
           ['青绿'	,'蜷缩'	,'沉闷'	,'稍糊'	,'稍凹'	,'硬滑'	,'坏瓜']]

A = ['色泽','根蒂','敲声','纹理','脐部','触感']

dataSet1 = [[1, 1, 'yes'],
               [1, 1, 'yes'],
               [1, 0, 'no'],
               [0, 1, 'no'],
               [0, 1, 'no']]
labels = ['no surfacing','flippers']

def isEqual(D):# 判断所有样本是否在所有的属性上取值相同
    for i in range(len(D)):#遍历样例
        for j in range(i+1,len(D)):#遍历之后的样例
            for k in range(len(D[i])-1):#遍历属性
                if D[i][k] != D[j][k]:
                    return False
                else:
                    continue
    return True

def mostClass(cList):
    classCount={}#计数器
    for className in cList:
        if className not in classCount.keys():
            classCount[className] = 0
        classCount[className] += 1
    sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1), reverse=True)
    print(sortedClassCount[0][0])
    return sortedClassCount[0][0]

def Ent(dataSet):
    sampleNum = len(dataSet)#样例总数
    classCount = {}#类标签计数器
    for sample in dataSet:
        curLabel = sample[-1]#当前的类标签是样例的最后一列
        if curLabel not in classCount.keys():
            classCount[curLabel] = 0
        classCount[curLabel] += 1
    infoEnt = 0.0# 初始化信息熵
    for key in classCount.keys():
        prob = float(classCount[key])/sampleNum
        infoEnt -= prob * log(prob,2)
    return infoEnt

def splitD(dataSet,value,index):
    retDataSet = []
    for sample in dataSet:  # 遍历数据集，并抽取按axis的当前value特征进划分的数据集(不包括axis列的值)
        if sample[index] == value:  #
            reducedFeatVec = sample[:index]
            reducedFeatVec.extend(sample[index + 1:])
            retDataSet.append(reducedFeatVec)
            # print axis,value,reducedFeatVec
    if retDataSet == []:#如果为空集返回当前集合
        return dataSet
    return retDataSet

def chooseBestAttrToSplit(dataSet):
    #属性数量
    attrsNum = len(dataSet[0])-1
    #print(range(attrsNum))
    #计算信息熵
    entD = Ent(dataSet)
    #计算信息增益
    bestInfoGain = 0.0
    bestAttr = -1
    for i in range(attrsNum): #遍历每个样例的当前属性的属性值加入集合i
        attrList = [sample[i] for sample in dataSet]
        attrsValue = set(attrList)
        entDA = 0.0 # 初始化条件熵
        for value in attrsValue:#计算条件熵
            subDataSet = splitD(dataSet,value,i)#按属性值划分子集
            weight = len(subDataSet)/float(len(dataSet))#计算权重
            entDA += weight * Ent(subDataSet)
        infoGain = entD - entDA
        if(infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestAttr = i
    return bestAttr
        #选取信息增益最大的属性

parent = []

def treeGenerate(D,A):
    CnameList = [sample[-1] for sample in D]#遍历每一个样例，将每个样例的类标签组成一个集合
    if CnameList.count(CnameList[0]) == len(CnameList):#当结点包含的样本全属于同一类别，无需划分，直接返回类标签
        return CnameList[0]
    if len(A) == 0 or isEqual(D):#如果A为空集或者所有样本在所有属性上取值相同，则无法划分，返回所含样本最多的类别
        return mostClass(CnameList)
    #从A中选择最优的划分属性
    bestAttrIndex = chooseBestAttrToSplit(D) #获取最优属性下标
    bestAttrName = A[bestAttrIndex]#获取最优属性名字
    #使用字典存储树信息
    treeDict = {bestAttrName:{}}
    del(A[bestAttrIndex])# 删除已经选取的特征
    attrList = [sample[bestAttrIndex] for sample in D] #获取每个样例最佳划分属性的属性值列表
    attrsValue = set(attrList)
    for value in attrsValue:
        subA = A[:]
        if len(D) == 0:#如果子集D为空集则，返回父集中样本最多的类
            return mostClass(CnameList)
        else:
            treeDict[bestAttrName][value] = treeGenerate(splitD(D,value,bestAttrIndex),subA)
    return treeDict

if __name__ == '__main__':
    tree = treeGenerate(dataSet,A)
    treePlotter.createPlot(tree)

绘图结果

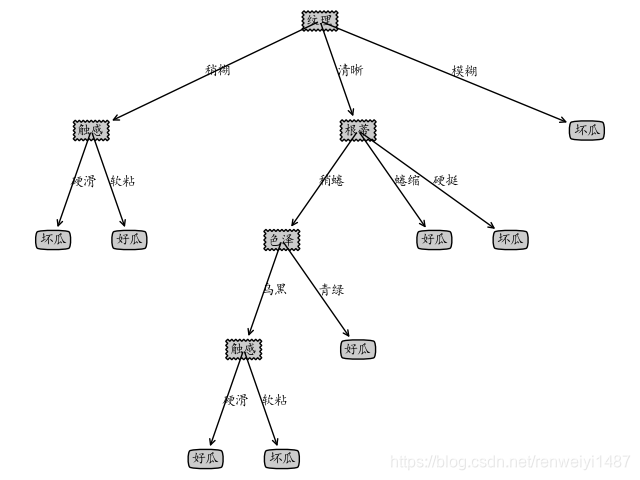
参考博客

[1]决策树算法及Python实现
[2]Pandas matplotlib 画图无法显示中文字体的问题
[3]西瓜书