解数独（Python）

0.目录

1.介绍

2.一些通用函数

3.全局变量（宏变量）

4.数独预处理（约束传播）

5.解数独（深度优先搜索+最小代价优先）

6.主函数

7.总代码

1.介绍

数独是一个非常有趣味性的智力游戏，数独起源于18世纪初瑞士数学家欧拉等人研究的拉丁方阵（Latin Square）。
参与者需要根据9×9盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行、每一列、每一个宫内的数字均含1-9，不重复。
一个数独谜题是由81个方块组成的网格。大部分爱好者把列标为1-9，把行标为A-I，把9个方块的一组（列，行，或者方框）称为一个单元，把处于同一单元的方块称为对等方块。谜题中有些方块是空白的，其他的填入了数字。
每个方块都属于3个单元，有20个对等方块。
当每个单元的方块填入了1到9的一个排列时，谜题就解决了。
本文采用解空间搜索的深度优先搜索（最小代价优先）加约束传播算法来解数独。
代码总体分为五个部分：
1.通用函数
2.全局变量（宏变量）
3.数独预处理（约束传播）
4.解数独（深度优先搜索+最小代价优先）
5.主函数

2.一些通用函数

import time

def cross(A, B):
    # 例如：A = 'ABC', B = '123'
    # 则返回['A1', 'A2', 'A3', 'B1', 'B2', 'B3', 'C1', 'C2', 'C3']
    return [a+b for a in A for b in B]

def arr_to_dict(A, B):
    # 例如：A = ['A', 'B', 'C'], B = ['1', '2', '3']
    # 则返回{'A': '1', 'B': '2', 'C': '3'}
    return dict(zip(A, B))

def str_to_arr(str_sudoku):
    # 传入：str_sudoku = '4.....8.5.3..........7......2.....6.....8.4......1.......6.3.7.5..2.....1.4......'
    # 返回['4', '.', '.', '.', '.', '.', '8', ... , '.', '.']
    return [c for c in str_sudoku if c in cols or c in '0.']

def show_str_sudoku(str_sudoku):
    # 解析字符串形式的数独并展示
    for i, value in enumerate(str_sudoku):
        if i%3 == 0 and i%9 != 0:
            print('|', end=' ')
        print(value, end=' ')
        if (i+1)%9 == 0:
            print()
        if i == 26 or i == 53:
            print('------+-------+------')

def show_dict_sudoku(dict_sudoku):
    # 解析字典形式的数独并展示
    width = 1 + max(len(dict_sudoku[s]) for s in squares)
    line = '+'.join(['-' * (width * 3)] * 3)
    for r in rows:
        print(''.join(dict_sudoku[r + c].center(width) + ('|' if c in '36' else '') for c in cols))
        if r in 'CF': print(line)
    print()

cross函数：输出A、B交叉组合而成的字符串
arr_to_dict函数：将数组形式的数独转化为字典形式的数独
str_to_arr函数：将字符串形式的数独转化为数组形式的数独
show_str_sudoku函数：解析字符串形式的数独并显示
show_dict_sudoku函数：解析字典形式的数独并显示

3.全局变量（宏变量）

用Python按如下方式来实现单元、对等方块、方块的概念：

cols = '123456789'
rows = 'ABCDEFGHI'
# squares表示 9*9个元素编号:['A1', 'A2', 'A3', ... , 'I8', 'I9']
squares = cross(rows, cols)
# unitlist表示 3*9个单元列表:
unitlist = ([cross(rows, c) for c in cols] + [cross(r, cols) for r in rows] + [cross(rs, cs) for rs in ('ABC','DEF','GHI') for cs in ('123','456','789')])
# units表示 某个元素编号:与之相关的3个单元列表
units = dict((s, [u for u in unitlist if s in u]) for s in squares)
# peers表示 某个元素编号:与之相关的20个元素编号
peers = dict((s, set(sum(units[s], []))-set([s])) for s in squares)

squares代表81个元素编号
unitlist代表27个不能出现重复数字的单元
units表示某个元素编号以及与之对应的3个单元列表
peers表示某个元素编号以及与之相关的20个元素编号

4.数独预处理（约束传播）

初始数独的样子：

以下是简单的预处理函数：

# 一.数独预处理
def parse_sudoku(str_sudoku):
    # values代表各位置上可能的取值:{'A1': '123456789', 'A2': '123456789', ... , 'I8': '123456789', 'I9': '123456789'}
    values = dict((s, cols) for s in squares)
    # arr_sudoku为数组形式, dict_sudoku为字典形式, 均为81位
    arr_sudoku = str_to_arr(str_sudoku)
    dict_sudoku = arr_to_dict(squares, arr_sudoku)# {'A1': '4', 'A2': '.', ... , 'I8': '.', 'I9': '.'}

    for key,value in dict_sudoku.items():
        if value in cols and not assign(values, key, value):
            return False

    return values

def assign(values, key, value):
    # 从values[key]中删除除了value以外的所有值，因为value是唯一的值
    # 如果在过程中发现矛盾，则返回False
    other_values = values[key].replace(value, '')
    if all(eliminate(values, key, num) for num in other_values):
        return values
    else:
        return False

def eliminate(values, key, num):
    # 从values[key]中删除值num，因为num是不可能的
    if num not in values[key]:
        return values
    values[key] = values[key].replace(num, '')

    return values

共三个函数。values[key]代表在key这个位置上的可能取值。
parse_sudoku函数：预处理的入口函数
assign函数：从values[key]中删除除了value以外的所有值
eliminate函数：从values[key]中删除值num
处理完后的数独为：

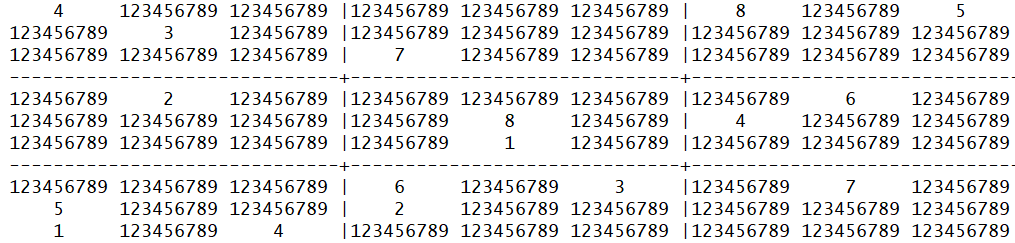
以上只是简单的进行的数独的预处理。
但是其实根据数独的规则，我们可以得到以下两条原则：
(1).如果一个方块只有一个可能值，把这个值从方块的对等方块（的可能值）中排除;
(2).如果一个单元只有一个可能位置来放某个值，就把值放那。
于是我们根据这个策略可以改写eliminate函数：

def eliminate(values, key, num):
    # 从values[key]中删除值num，因为num是不可能的
    if num not in values[key]:
        return values
    values[key] = values[key].replace(num, '')

    # 这里采用了约束传播
    # 1.如果一个方块只有一个可能值，把这个值从方块的对等方块（的可能值）中排除。
    if len(values[key]) == 0:
        return False
    elif len(values[key]) == 1:
        only_value = values[key]
        # 从与之相关的20个元素中删除only_value
        if not all(eliminate(values, peer, only_value) for peer in peers[key]):
            return False

    # 2.如果一个单元只有一个可能位置来放某个值，就把值放那。
    for unit in units[key]:
        dplaces = [s for s in unit if num in values[s]]
        if len(dplaces) == 0:
            return False
        elif len(dplaces) == 1:
            only_key = dplaces[0]
            if not assign(values, only_key, num):
                return False

    return values

于是数独的预处理结果变为了：

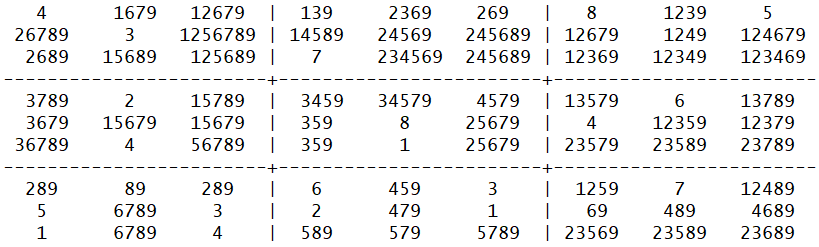
这样是不是就把问题规模一下子简化了很多。

5.解数独（深度优先搜索+最小代价优先）

因为没有规定数独只有唯一解，所以以下程序实际上求解了数独的所有解。

# 二.解数独
def solve_sudoku(str_sudoku):
    return search_sudoku(parse_sudoku(str_sudoku))

def search_sudoku(values):
    if values is False:
        return False
    if all(len(values[s]) == 1 for s in squares):
        return values

    # 选择可能值数目最少的方块, 进行深度优先搜索
    n, key = min((len(values[key]), key) for key in squares if len(values[key]) > 1)
    return some_result(search_sudoku(assign(values.copy(), key, num)) for num in values[key])

def some_result(values):
    for result in values:
        if result:
            return result
    return False

solve_sudoku函数：是真正的解数独的入口，将数独预处理完毕的结果抛给search_sudoku函数求解
search_sudoku函数：是一个递归函数，采用的代价函数是选择可能值数目最少的方块，然后进行深度优先搜索遍历。
some_result函数：是在深度优先搜索的结果中找出满足条件的数独返回。如果想要所有解，那么可以改成返回一个解的列表。
如果想要程序更快，那么就可以只找一个解。可以在深度优先搜索的循环代码中，返回找到的满足条件的解即可。

6.主函数

if __name__ == '__main__':
    # str_sudoku为字符串形式, 为81位
    str_sudoku = ['4.....8.5.3..........7......2.....6.....8.4......1.......6.3.7.5..2.....1.4......']
    # str_sudoku = ['4.....8.5.3..........7......2.....6.....8.4......1.......6.3.7.5..2.....1.4......',
    #               '003020600900305001001806400008102900700000008006708200002609500800203009005010300',
    #               '.....6....59.....82....8....45........3........6..3.54...325..6..................']

    for sudoku in str_sudoku:
        start = time.clock()
        solve_result = solve_sudoku(sudoku)
        end = time.clock()
        print('初始数独为：')
        show_str_sudoku(sudoku)
        print('解为：')
        show_dict_sudoku(solve_result)
        print("求解数独运行时间为: %f s" % (end - start))

解出来数独的结果为：

7.总代码

'''
    数独是一个非常有趣味性的智力游戏
    参与者需要根据9×9盘面上的已知数字，推理出所有剩余空格的数字，
    并满足每一行、每一列、每一个宫内的数字均含1-9，不重复。
'''
__author__ = 'PyLearn'
import time

def cross(A, B):
    # 例如：A = 'ABC', B = '123'
    # 则返回['A1', 'A2', 'A3', 'B1', 'B2', 'B3', 'C1', 'C2', 'C3']
    return [a+b for a in A for b in B]

def arr_to_dict(A, B):
    # 例如：A = ['A', 'B', 'C'], B = ['1', '2', '3']
    # 则返回{'A': '1', 'B': '2', 'C': '3'}
    return dict(zip(A, B))

def str_to_arr(str_sudoku):
    # 传入：str_sudoku = '4.....8.5.3..........7......2.....6.....8.4......1.......6.3.7.5..2.....1.4......'
    # 返回['4', '.', '.', '.', '.', '.', '8', ... , '.', '.']
    return [c for c in str_sudoku if c in cols or c in '0.']

def show_str_sudoku(str_sudoku):
    # 解析字符串形式的数独并展示
    for i, value in enumerate(str_sudoku):
        if i%3 == 0 and i%9 != 0:
            print('|', end=' ')
        print(value, end=' ')
        if (i+1)%9 == 0:
            print()
        if i == 26 or i == 53:
            print('------+-------+------')

def show_dict_sudoku(dict_sudoku):
    # 解析字典形式的数独并展示
    width = 1 + max(len(dict_sudoku[s]) for s in squares)
    line = '+'.join(['-' * (width * 3)] * 3)
    for r in rows:
        print(''.join(dict_sudoku[r + c].center(width) + ('|' if c in '36' else '') for c in cols))
        if r in 'CF': print(line)
    print()

cols = '123456789'
rows = 'ABCDEFGHI'
# squares表示 9*9个元素编号:['A1', 'A2', 'A3', ... , 'I8', 'I9']
squares = cross(rows, cols)
# unitlist表示 3*9个单元列表:
unitlist = ([cross(rows, c) for c in cols] + [cross(r, cols) for r in rows] + [cross(rs, cs) for rs in ('ABC','DEF','GHI') for cs in ('123','456','789')])
# units表示 某个元素编号:与之相关的3个单元列表
units = dict((s, [u for u in unitlist if s in u]) for s in squares)
# peers表示 某个元素编号:与之相关的20个元素编号
peers = dict((s, set(sum(units[s], []))-set([s])) for s in squares)

# 一.数独预处理
def parse_sudoku(str_sudoku):
    # values代表各位置上可能的取值:{'A1': '123456789', 'A2': '123456789', ... , 'I8': '123456789', 'I9': '123456789'}
    values = dict((s, cols) for s in squares)
    # arr_sudoku为数组形式, dict_sudoku为字典形式, 均为81位
    arr_sudoku = str_to_arr(str_sudoku)
    dict_sudoku = arr_to_dict(squares, arr_sudoku)# {'A1': '4', 'A2': '.', ... , 'I8': '.', 'I9': '.'}

    for key,value in dict_sudoku.items():
        if value in cols and not assign(values, key, value):
            return False

    return values

def assign(values, key, value):
    # 从values[key]中删除除了value以外的所有值，因为value是唯一的值
    # 如果在过程中发现矛盾，则返回False
    other_values = values[key].replace(value, '')
    if all(eliminate(values, key, num) for num in other_values):
        return values
    else:
        return False

def eliminate(values, key, num):
    # 从values[key]中删除值num，因为num是不可能的
    if num not in values[key]:
        return values
    values[key] = values[key].replace(num, '')

    # 这里采用了约束传播
    # 1.如果一个方块只有一个可能值，把这个值从方块的对等方块（的可能值）中排除。
    if len(values[key]) == 0:
        return False
    elif len(values[key]) == 1:
        only_value = values[key]
        # 从与之相关的20个元素中删除only_value
        if not all(eliminate(values, peer, only_value) for peer in peers[key]):
            return False

    # 2.如果一个单元只有一个可能位置来放某个值，就把值放那。
    for unit in units[key]:
        dplaces = [s for s in unit if num in values[s]]
        if len(dplaces) == 0:
            return False
        elif len(dplaces) == 1:
            only_key = dplaces[0]
            if not assign(values, only_key, num):
                return False

    return values

# 二.解数独
def solve_sudoku(str_sudoku):
    return search_sudoku(parse_sudoku(str_sudoku))

def search_sudoku(values):
    if values is False:
        return False
    if all(len(values[s]) == 1 for s in squares):
        return values

    # 选择可能值数目最少的方块, 进行深度优先搜索
    n, key = min((len(values[key]), key) for key in squares if len(values[key]) > 1)
    return some_result(search_sudoku(assign(values.copy(), key, num)) for num in values[key])

def some_result(values):
    for result in values:
        if result:
            return result
    return False

if __name__ == '__main__':
    # str_sudoku为字符串形式, 为81位
    str_sudoku = ['4.....8.5.3..........7......2.....6.....8.4......1.......6.3.7.5..2.....1.4......']
    # str_sudoku = ['4.....8.5.3..........7......2.....6.....8.4......1.......6.3.7.5..2.....1.4......',
    #               '003020600900305001001806400008102900700000008006708200002609500800203009005010300',
    #               '.....6....59.....82....8....45........3........6..3.54...325..6..................']

    for sudoku in str_sudoku:
        start = time.clock()
        solve_result = solve_sudoku(sudoku)
        end = time.clock()
        print('初始数独为：')
        show_str_sudoku(sudoku)
        print('解为：')
        show_dict_sudoku(solve_result)
        print("求解数独运行时间为: %f s" % (end - start))