数据结构开发(12):栈与队列
0.目录
1.栈的概念及实现
2.队列的概念及实现
3.两个有趣的问题
- 3.1 是否可以用栈实现队列?
- 3.2 是否可以用队列实现栈?
4.小结
1.栈的概念及实现
1.1 顺序栈的实现
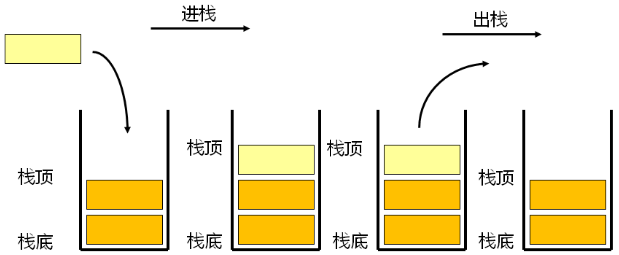
栈的定义:
- 栈是一种特殊的线性表
- 栈仅能在线性表的一端进行操作
- 栈顶(Top):允许操作的一端
- 栈底(Bottom):不允许操作的一端
栈的特点——后进先出( Last In First Out ):
栈的操作:
- 创建栈( Stack() )
- 销毁栈( ~Stack() )
- 清空栈( clear() )
- 进栈( push() )
- 出栈( pop() )
- 获取栈顶元素( top() )
- 获取栈的大小( size() )
栈的实现:

栈的顺序实现:
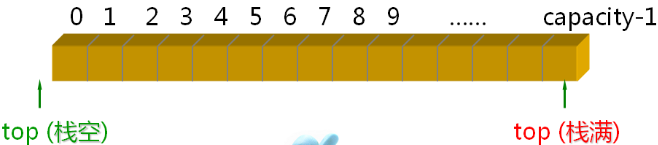
StaticStack 设计要点:
- 类模板
- 使用原生数组作为栈的存储空间
- 使用模板参数决定栈的最大容量

顺序栈的实现(在StLib项目中创建Stack.h和StaticStack.h):
Stack.h
#ifndef STACK_H
#define STACK_H
#include "Object.h"
namespace StLib
{
template <typename T>
class Stack : public Object
{
public:
virtual void push(const T& e) = 0;
virtual void pop() = 0;
virtual T top() const = 0;
virtual void clear() = 0;
virtual int size() const = 0;
};
}
#endif // STACK_H
StaticStack.h
#ifndef STATICSTACK_H
#define STATICSTACK_H
#include "Stack.h"
#include "Exception.h"
namespace StLib
{
template <typename T, int N>
class StaticStack : public Stack<T>
{
protected:
T m_space[N]; // 栈存储空间,N为模板参数
int m_top; // 栈顶标识
int m_size; // 当前栈大小
public:
StaticStack()
{
m_top = -1;
m_size = 0;
}
int capacity() const
{
return N;
}
void push(const T& e)
{
if( m_size < N )
{
m_space[m_top + 1] = e;
m_top++;
m_size++;
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No space in current stack ...");
}
}
void pop()
{
if( m_size > 0 )
{
m_top--;
m_size--;
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No element in current stack ...");
}
}
T top() const
{
if( m_size > 0 )
{
return m_space[m_top];
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No element in current stack ...");
}
}
void clear()
{
m_top = -1;
m_size = 0;
}
int size() const
{
return m_size;
}
};
}
#endif // STATICSTACK_H
main.cpp测试
#include <iostream>
#include "StaticStack.h"
using namespace std;
using namespace StLib;
int main()
{
StaticStack<int, 5> stack;
try
{
stack.pop();
}
catch(const Exception& e)
{
cout << e.message() << endl;
cout << e.location() << endl;
}
for(int i=0; i<5; i++)
{
stack.push(i);
}
while( stack.size() > 0 )
{
cout << stack.top() << endl;
stack.pop();
}
return 0;
}
运行结果为:
No element in current stack ...
f:\allcode\qtcreator\datastructure\stlib\StaticStack.h:52
4
3
2
1
0
(StaticStack是有缺陷的。当存储的元素为类类型时,StaticStack的对象在创建时,会多次调用元素类型的构造函数,影响效率。)
示例——StaticStack的缺陷:
#include <iostream>
#include "StaticStack.h"
using namespace std;
using namespace StLib;
class Test : public Object
{
public:
Test()
{
cout << "Test()" << endl;
}
~Test()
{
cout << "~Test()" << endl;
}
};
int main()
{
StaticStack<Test, 10> stack;
cout << stack.size() << endl;
return 0;
}
运行结果为:
Test()
Test()
Test()
Test()
Test()
Test()
Test()
Test()
Test()
Test()
0
~Test()
~Test()
~Test()
~Test()
~Test()
~Test()
~Test()
~Test()
~Test()
~Test()
1.2 链式栈的实现
链式栈的存储实现:
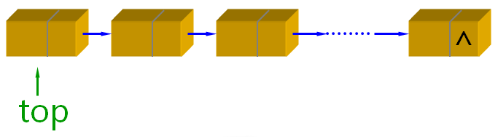
链式栈的设计要点:
- 类模板,抽象父类 Stack 的直接子类
- 在内部组合使用 LinkList 类,实现栈的链式存储
- 只在单链表成员对象的头部进行操作
链式栈的实现(在StLib项目中创建LinkStack.h):
LinkStack.h
#ifndef LINKSTACK_H
#define LINKSTACK_H
#include "Stack.h"
#include "LinkList.h"
namespace StLib
{
template <typename T>
class LinkStack : public Stack<T>
{
protected:
LinkList<T> m_list;
public:
void push(const T& e)
{
m_list.insert(0, e);
}
void pop()
{
if( m_list.length() > 0 )
{
m_list.remove(0);
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No element in current stack ...");
}
}
T top() const
{
if( m_list.length() > 0 )
{
return m_list.get(0);
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No element in current stack ...");
}
}
void clear()
{
m_list.clear();
}
int size() const
{
return m_list.length();
}
};
}
#endif // LINKSTACK_H
main.cpp测试
#include <iostream>
#include "LinkStack.h"
using namespace std;
using namespace StLib;
class Test : public Object
{
public:
Test()
{
cout << "Test()" << endl;
}
~Test()
{
cout << "~Test()" << endl;
}
};
int main()
{
LinkStack<Test> stack;
cout << stack.size() << endl;
return 0;
}
运行结果为:
0
栈的应用实践:
- 符号匹配问题
- 在C语言中有一些成对匹配出现的符号
- 括号:( ), [ ], { }, < >
- 引号:' ', " "
- 在C语言中有一些成对匹配出现的符号
问题——如何实现编译器中的符号成对检测?
算法思路:
- 从第一个字符开始扫描
- 当遇见普通字符时忽略
- 当遇见左符号时压入栈中
- 当遇见右符号时弹出栈顶符号,并进行匹配
- 结束
- 成功:所有字符扫描完毕,且栈为空
- 失败:匹配失败或所有字符扫描完毕但栈非空
符号匹配:
#include <iostream>
#include "LinkStack.h"
using namespace std;
using namespace StLib;
bool is_left(char c)
{
return (c == '(') || (c == '{') || (c == '[') || (c == '<');
}
bool is_right(char c)
{
return (c == ')') || (c == '}') || (c == ']') || (c == '>');
}
bool is_quot(char c)
{
return (c == '\'') || (c == '\"');
}
bool is_match(char l, char r)
{
return ( (l == '(') && (r == ')') ) ||
( (l == '{') && (r == '}') ) ||
( (l == '[') && (r == ']') ) ||
( (l == '<') && (r == '>') ) ||
( (l == '\'') && (r == '\'') ) ||
( (l == '\"') && (r == '\"') );
}
bool scan(const char* code)
{
LinkStack<char> stack;
int i = 0;
bool ret = true;
code = (code == NULL) ? "" : code;
while( ret && (code[i] != '\0') )
{
if( is_left(code[i]) )
{
stack.push(code[i]);
}
else if( is_right(code[i]) )
{
if( (stack.size() > 0) && is_match(stack.top(), code[i]) )
{
stack.pop();
}
else
{
ret = false;
}
}
else if( is_quot(code[i]) )
{
if( (stack.size() == 0) || !is_match(stack.top(), code[i]) )
{
stack.push(code[i]);
}
else if( is_match(stack.top(), code[i]) )
{
stack.pop();
}
}
i++;
}
return ret && (stack.size() == 0);
}
int main()
{
cout << scan("abcd") << endl;
cout << scan("<a{b(\'x\')c}d>") << endl;
cout << scan("({)}") << endl;
cout << scan("if((stack.size()==0)||!is_match(stack.top(),code[i])){stack.push(code[i]);}else if(is_match(stack.top(),code[i])){stack.pop();}") << endl;
return 0;
}
运行结果为:
1
1
0
1
深度思考——开放性问题:
- 使用单链表对象实现链式栈时,为什么选择在单链表的头部进行操作?如果选择在尾部进行操作是否也能实现栈的功能?
2.队列的概念及实现
2.1 队列的顺序实现
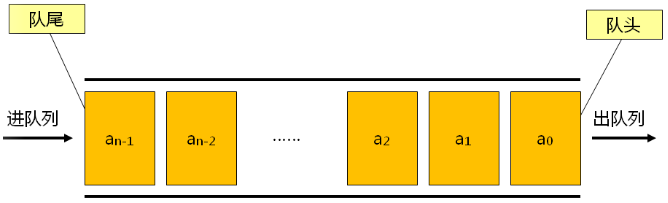
队列是一种特殊的线性表
队列仅能在线性表的两端进行操作
- 队头( Front ):取出数据元素的一端
- 队尾( Rear ):插入数据元素的一端
队列的特性——先进先出( First In First Out ):
队列的操作:
- 创建队列( Queue() )
- 销毁队列( ~Queue() )
- 清空队列( clear() )
- 进队列( add() )
- 出队列( remove() )
- 获取队头元素( front() )
- 获取队列的长度( length() )
队列的实现:

队列的顺序实现:
StaticQueue 设计要点:
- 类模板
- 使用原生数组作为队列的存储空间
- 使用模板参数决定队列的最大容量

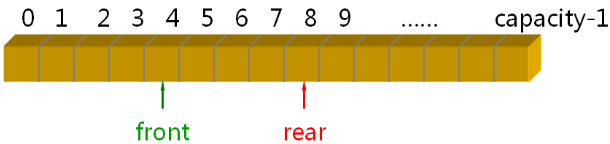
StaticQueue 实现要点(循环计数法):
- 关键操作
- 进队列:
m_space[m_rear] = e; m_rear = (m_rear + 1) % N; - 出队列:
m_front = (m_front + 1) % N;
- 进队列:
- 队列的状态
- 队空:
( m_length == 0 ) && ( m_front == m_rear ) - 队满:
( m_length == N ) && ( m_front == m_rear )
- 队空:
顺序栈的实现(在StLib项目中创建Queue.h和StaticQueue.h):
Queue.h
#ifndef QUEUE_H
#define QUEUE_H
#include "Object.h"
namespace StLib
{
template <typename T>
class Queue : public Object
{
public:
virtual void add(const T& e) = 0;
virtual void remove() = 0;
virtual T front() const = 0;
virtual void clear() = 0;
virtual int length() const = 0;
};
}
#endif // QUEUE_H
StaticQueue.h
#ifndef STATICQUEUE_H
#define STATICQUEUE_H
#include "Queue.h"
#include "Exception.h"
namespace StLib
{
template <typename T, int N>
class StaticQueue : public Queue<T>
{
protected:
T m_space[N]; // 队列存储空间,N为模板参数
int m_front; // 队头标识
int m_rear; // 队尾标识
int m_length; // 当前队列的长度
public:
StaticQueue()
{
m_front = 0;
m_rear = 0;
m_length = 0;
}
int capacity() const
{
return N;
}
void add(const T& e)
{
if( m_length < N )
{
m_space[m_rear] = e;
m_rear = (m_rear + 1) % N;
m_length++;
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No space in current queue ...");
}
}
void remove()
{
if( m_length > 0 )
{
m_front = (m_front + 1) % N;
m_length--;
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No element in current queue ...");
}
}
T front() const
{
if( m_length > 0 )
{
return m_space[m_front];
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No element in current queue ...");
}
}
void clear()
{
m_front = 0;
m_rear = 0;
m_length = 0;
}
int length() const
{
return m_length;
}
};
}
#endif // STATICQUEUE_H
main.cpp测试
#include <iostream>
#include "StaticQueue.h"
using namespace std;
using namespace StLib;
int main()
{
StaticQueue<int, 5> queue;
for(int i=0; i<5; i++)
{
queue.add(i);
}
while( queue.length() > 0 )
{
cout << queue.front() << endl;
queue.remove();
}
return 0;
}
运行结果为:
0
1
2
3
4
(StaticQueue也是有缺陷的。类似的,当数据元素为类类型,StaticQueue的对象在创建时,会多次调用元素类型的构造函数,影响效率。)
2.2 队列的链式实现
队列的链式存储实现:
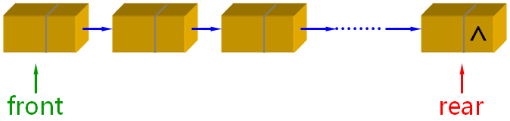
链式队列的设计要点:
- 类模板,抽象父类 Queue 的直接子类
- 在内部使用链式结构实现元素的存储
- 只在链表的头部和尾部进行操作
队列的链式实现(LinkQueue.h):
LinkQueue.h
#ifndef LINKQUEUE_H
#define LINKQUEUE_H
#include "Queue.h"
#include "LinkList.h"
namespace StLib
{
template <typename T>
class LinkQueue : public Queue<T>
{
protected:
LinkList<T> m_list;
public:
void add(const T& e)
{
m_list.insert(e);
}
void remove()
{
if( m_list.length() > 0 )
{
m_list.remove(0);
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No element in current queue ...");
}
}
T front() const
{
if( m_list.length() > 0 )
{
return m_list.get(0);
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No element in current queue ...");
}
}
void clear()
{
m_list.clear();
}
int length() const
{
return m_list.length();
}
};
}
#endif // LINKQUEUE_H
main.cpp测试
#include <iostream>
#include "LinkQueue.h"
using namespace std;
using namespace StLib;
int main()
{
LinkQueue<int> lq;
for(int i=0; i<5; i++)
{
lq.add(i);
}
while( lq.length() > 0 )
{
cout << lq.front() << endl;
lq.remove();
}
return 0;
}
运行结果为:
0
1
2
3
4
问题:
使用 LinkList 类实现链式队列是否合适,是否有更好的方案?
(链式队列的性能比较差,并不高效。插入操作经历了遍历的过程!时间复杂度为O(n)。)
队列链式存储实现的优化:

链式队列的设计优化:
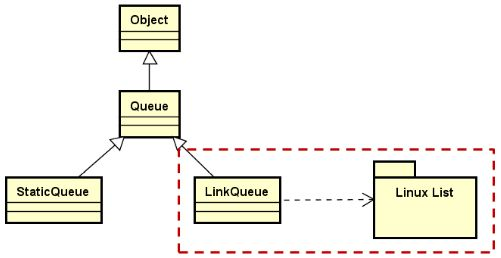
基于Linux内核链表的队列:
LinkQueue.h
#ifndef LINKQUEUE_H
#define LINKQUEUE_H
#include "Queue.h"
#include "LinuxList.h"
#include "Exception.h"
namespace StLib
{
template <typename T>
class LinkQueue : public Queue<T>
{
protected:
struct Node : public Object
{
list_head head;
T value;
};
list_head m_header;
int m_length;
public:
LinkQueue()
{
m_length = 0;
INIT_LIST_HEAD(&m_header);
}
void add(const T& e)
{
Node* node = new Node();
if( node != NULL )
{
node->value = e;
list_add_tail(&node->head, &m_header);
m_length++;
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No memory to add new element ...");
}
}
void remove()
{
if( m_length > 0 )
{
list_head* toDel = m_header.next;
list_del(toDel);
m_length--;
delete list_entry(toDel, Node, head);
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No element in current queue ...");
}
}
T front() const
{
if( m_length > 0 )
{
return list_entry(m_header.next, Node, head)->value;
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No element in current queue ...");
}
}
void clear()
{
while( m_length > 0 )
{
remove();
}
}
int length() const
{
return m_length;
}
~LinkQueue()
{
clear();
}
};
}
#endif // LINKQUEUE_H
main.cpp测试
#include <iostream>
#include "LinkQueue.h"
using namespace std;
using namespace StLib;
class Test : public Object
{
public:
Test()
{
cout << "Test()" << endl;
}
~Test()
{
cout << "~Test()" << endl;
}
};
int main()
{
LinkQueue<Test> lq;
cout << lq.length() << endl;
return 0;
}
运行结果为:
0
3.两个有趣的问题
3.1 是否可以用栈实现队列?
问题:
- 栈和队列在实现上非常类似,是否可以用栈实现队列?
问题分析:
- 用栈实现队列等价于用“后进先出”的特性实现“先进先出”的特性!
解决方案设计:
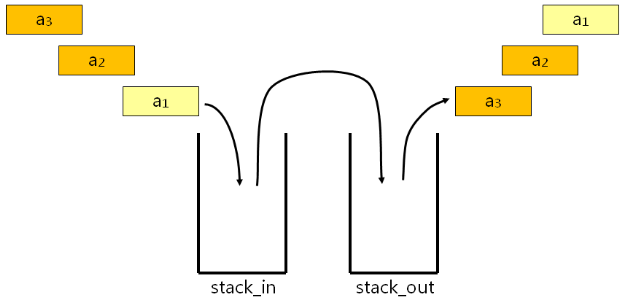
实现思路:
- 准备两个栈用于实现队列:stack_in 和 stack_out
- 当有新元素入队时:将其压入 stack_in
- 当需要出队时:
stack_out.size() == 0:- 将 stack_in 中的元素逐一弹出并压入 stack_out
- 将 stack_out 的栈顶元素弹出
stack_out.size() > 0:- 将 stack_out 的栈顶元素弹出
用栈实现队列(实现StackToQueue类):
#include <iostream>
#include "LinkStack.h"
#include "LinkQueue.h"
using namespace std;
using namespace StLib;
template <typename T>
class StackToQueue : public Queue<T>
{
protected:
mutable LinkStack<T> m_stack_in;
mutable LinkStack<T> m_stack_out;
void move() const
{
if( m_stack_out.size() == 0 )
{
while( m_stack_in.size() > 0 )
{
m_stack_out.push(m_stack_in.top());
m_stack_in.pop();
}
}
}
public:
void add(const T& e)
{
m_stack_in.push(e);
}
void remove()
{
move();
if( m_stack_out.size() > 0 )
{
m_stack_out.pop();
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No element in current queue ...");
}
}
T front() const
{
move();
if( m_stack_out.size() > 0 )
{
return m_stack_out.top();
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No element in current queue ...");
}
}
void clear()
{
m_stack_in.clear();
m_stack_out.clear();
}
int length() const
{
return m_stack_in.size() + m_stack_out.size();
}
};
int main()
{
StackToQueue<int> sq;
for(int i=0; i<5; i++)
{
sq.add(i);
}
while( sq.length() > 0 )
{
cout << sq.front() << endl;
sq.remove();
}
return 0;
}
运行结果为:
0
1
2
3
4
(虽然能用栈实现队列,但是效率不高。)
3.2 是否可以用队列实现栈?
问题:
- 反之,是否可以用队列实现栈?
问题分析:
- 本质为,用队列“先进先出”的特性实现栈“后进先出”的特性!
解决方案设计:
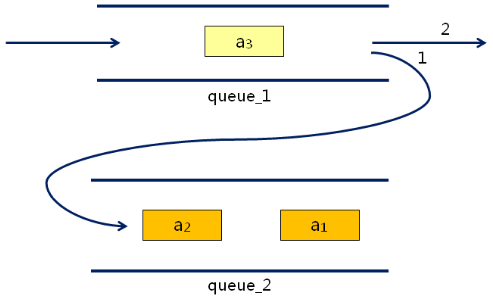
实现思路:
- 准备两个队列用于实现栈:queue_1 [in] 和 queue_2 [out]
- 当有新元素入栈时:将其加入队列 [in]
- 当需要出栈时:
- 将队列 [in] 中的 n-1 个元素出队列,并进入队列 [out] 中
- 将队列 [in] 中的最后一个元素出队列(出栈)
- 交换两个队列的角色:queue_1 [out] 和 queue_2 [in]
用队列实现栈(实现QueueToStack类):
#include <iostream>
#include "LinkStack.h"
#include "LinkQueue.h"
using namespace std;
using namespace StLib;
template <typename T>
class QueueToStack : public Stack<T>
{
protected:
mutable LinkQueue<T> m_queue_1;
mutable LinkQueue<T> m_queue_2;
LinkQueue<T>* m_pIn;
LinkQueue<T>* m_pOut;
void move() const
{
int n = m_pIn->length() - 1;
for(int i=0; i<n; i++)
{
m_pOut->add(m_pIn->front());
m_pIn->remove();
}
}
void swap()
{
LinkQueue<T>* temp = NULL;
temp = m_pIn;
m_pIn = m_pOut;
m_pOut = temp;
}
public:
QueueToStack()
{
m_pIn = &m_queue_1;
m_pOut = &m_queue_2;
}
void push(const T& e)
{
m_pIn->add(e);
}
void pop()
{
if( m_pIn->length() > 0 )
{
move();
m_pIn->remove();
swap();
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No element in current stack ...");
}
}
T top() const
{
if( m_pIn->length() > 0 )
{
move();
return m_pIn->front();
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No element in current stack ...");
}
}
void clear()
{
m_queue_1.clear();
m_queue_2.clear();
}
int size() const
{
return m_queue_1.length() + m_queue_2.length();
}
};
int main()
{
QueueToStack<int> qs;
for(int i=0; i<5; i++)
{
qs.push(i);
}
while( qs.size() > 0 )
{
cout << qs.top() << endl;
qs.pop();
}
return 0;
}
运行结果为:
4
3
2
1
0
(虽然能用队列实现栈,但是效率不高。)
4.小结
- 栈是一种特殊的线性表
- 栈只允许在线性表的一端进行操作
- StaticStack 使用原生数组作为内部存储空间
- StaticStack 的最大容量由模板参数决定
- 链式栈的实现组合使用了单链表对象
- 在单链表的头部进行操作能够实现高效的入栈和出栈操作
- 栈“后进先出”的特性适用于检测成对出现的符号
- 栈非常适合于需要“就近匹配”的场合
- 队列是一种特殊的线性表,具有先进先出的特性
- 队列只允许在线性表的两端进行操作,一端进,一端出
- StaticQueue 使用原生数组作为内部存储空间
- StaticQueue 的最大容量由模板参数决定
- StaticQueue 采用循环计数法提高队列操作的效率
- StaticQueue 在初始化时可能多次调用元素类型的构造函数
- LinkList 的组合使用能够实现队列的功能,但是不够高效
- LinkQueue 的最终实现组合使用了Linux内核链表
- LinkQueue 中入队和出队操作可以在常量时间内完成
- 栈和队列在实现上非常类似,可以相互转化实现
- 两个栈“后进先出”叠加得到“先进先出”的特性
- 两个队列“先进先出”相互配合得到“后进先出”的特性
- 栈和队列相互转化的学习有助于强化本质的理解


 浙公网安备 33010602011771号
浙公网安备 33010602011771号