[洛谷 P3376] 网络最大流 | 模板 Edmonds Karp(EK算法) 入门

题目链接

题目描述

如题，给出一个网络图，以及其源点和汇点，求出其网络最大流。

输入格式

第一行包含四个正整数 $n$,$m$,$s$,$t$，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含三个正整数 u_i ,v_i,w_i ，表示第 i 条有向边从 u_i 出发，到达 v_i，边权为 w_i即该边最大流量为 w_i）。
输出格式

一行，包含一个正整数，即为该网络的最大流。
输入输出样例

4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 40

50

样例输入输出 1 解释

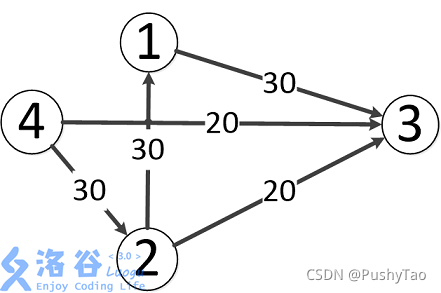
以下代码来源于《算法竞赛入门指南》

在最大流问题中，容量$c$和流量$f$满足三个性质：容量限制，即$f(u,v)$ $\le$ $c(u,v)$、斜对称性即 $f(u,v)$ = $-$ $f(v,u)$和流量平衡(对于除了节点$s$ 和 节点$t$ 外的任意节点$u$，$$\sum _{(u,v)\in E}f(u,v)=0$$)。
问题的目标是最大化 $|f|$ = $$\sum _{(s,v)\in E}f(s,v)=\sum _{(u,t)\in E}f(u,t)$$，即从$s$点流出的净流量（其也等于流入$t$点的净流量）。

算法思想：
从零流（所有边的流量均为0）开始不断增加流量，保持每次增加流量之后，都满足容量限制、斜对称性和流量平衡三个条件。
称每条边上容量与流量之差为残余容量，简称残量
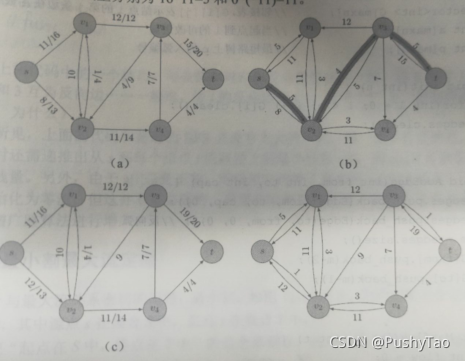
根据下图$a$得到残量网络$b$，同样的可以由$c$得到$d$。
注意残量网络中的边数可能达到原图中的边数的两倍，在原图中：$c=16$,$f=11$的边在残量网络中对应正反两条边，残量分别为$16-11=5$和$0-(-11)=11$

该算法基于这样一个事实：残量网络中任意一条从$s$到$t$的有向道路都对应一条原图中的增广路，只需要求出该道路中所有残量的最小值$d$，把对应的所有边上的流量增加$d$即可，这个过程称为增广过程。如果增广前的流量满足三个条件，增广后依然满足。显然，只要残量网络中存在增广路，流量就可以增大。可以证明他的逆命题也成立：如果残量网络中不存在增广路，则当前流就是最大流。这便是著名的增广路定理

当且仅当残量网络中不存在$s$$-$$t$的有向道路(增广路)时，此时的流时从$s$到$t$的最大流

struct Edge {
	int u, v;
	ll cap, flow;
	Edge(int uu, int vv, ll _cap, ll _flow) {
		u = uu, v = vv, cap = _cap, flow = _flow;
	}
};
struct EdmondsKarp {
	ll n, m;
	vector<Edge> edges;
	vector<int> G[maxn];
	ll a[maxn], p[maxn];
	void init(int n) {
		for (int i = 0; i <= n; i++) G[i].clear();
		edges.clear();
	}
	void add(int u, int v, ll cap) {
		edges.push_back(Edge(u, v, cap, 0));
		edges.push_back(Edge(v, u, 0, 0));
		m = edges.size();
		G[u].push_back(m - 2);
		G[v].push_back(m - 1);
	}
	ll maxFlow(int s, int t) {
		ll Flow = 0;
		while (true) {
			memset(a, 0, sizeof a);
			queue<int> que;
			que.push(s);
			a[s] = INF;
			while (que.size()) {
				int u = que.front();
				que.pop();
				for (int i = 0; i < G[u].size(); i++) {
					int id = G[u][i];
					Edge &e = edges[id];///不加&也是可以的
					int to = e.v;
					if (!a[to] && e.cap > e.flow) {
						p[to] = id;
						a[to] = min(a[u], e.cap - e.flow);
						que.push(to);
					}
				}
				if (a[t]) break;
			}
			if (!a[t]) break;
			for (int u = t; u != s; u = edges[p[u]].u) {
				edges[p[u]].flow += a[t];
				edges[p[u] ^ 1].flow -= a[t];
			}
			Flow += a[t];
		}
		return Flow;
	}
} slove;
int n, m, s, t;
int main() {
	cin >> n >> m >> s >> t;
	slove.init(n);
	slove.n = n;
	for (int i = 1; i <= m; i++) {
		int u = read, v = read;
		ll cap = read;
		slove.add(u,v,cap);
	}
	
	cout << slove.maxFlow(s,t) <<endl;
	return 0;
}