Deep Learning-深度学习（六）

深度学习进阶

1、卷积神经网络基础

　　在之前的手写数字识别中，运用全连接的神经网络会有两个问题，即①图片输入之后空间信息会缺失；②模型的参数过多会发生过拟合的现象。为了弥补这种错误，于是引入了卷积神经网络。

1.1 卷积计算

　　卷积，数学分析中的一种积分变换的方法。在卷积神经网络中，卷积神经网络中，卷积层的实现方式是数学中的互相关运算，这与数学分析中的卷积有所不同，运算过程如图所示：

　　

 

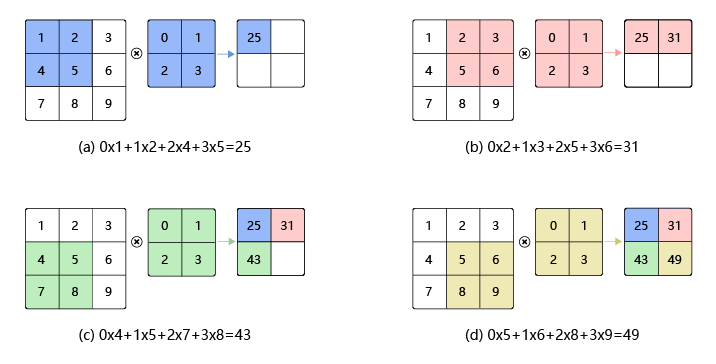
　　其中，卷积核也称作滤波器，假设卷积核的高和宽分别是K(h)和K(w)，则将称为K(h)×K(w)卷积。如上图所示，每一组2×2的数组即为卷积核，通过滑动，从而得到四个值a,b,c,d。

　　卷积核的计算过程为：

　　

　　其中， a 代表输入图片， b 代表输出特征图，w 是卷积核参数，它们都是二维数组，∑u,v  表示对卷积核参数进行遍历并求和。

　　以上图为例，其中的u，v就都能分别取0和1，即卷积核的长宽所能的长度，该例子计算如下：

 

　　

 

　　

　　此外，需要注意的是，卷积的每一步有时还有添加偏置的步骤，即加一个余项。

 

1.2 填充

 

　　在上面的例子中，输入图片尺寸为3×3，输出图片尺寸为2×2，经过一次卷积之后，图片尺寸变小。卷积输出特征图的尺寸计算方法如下（卷积核的高和宽分别为kh和kw​）：

　　

 

 

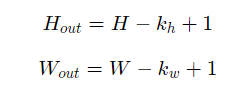
 　　即如果输入尺寸为4，卷积核大小为3时，输出尺寸为4−3+1=2。因为通过卷积过后，图片的大小会减小，为了避免图片变小，通常会在外围进行填充，如下图：

　　

 

　　

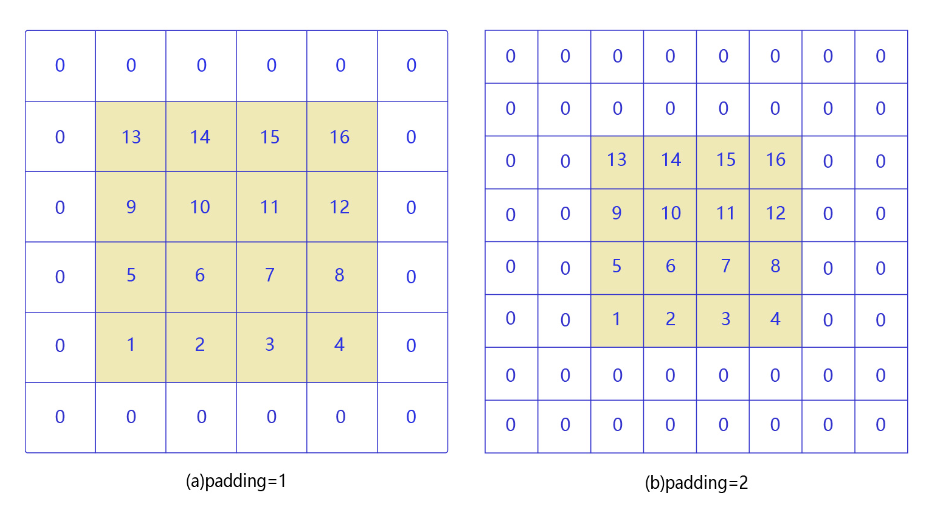
  • 如图（a）所示：填充的大小为1，填充值为0。填充之后，输入图片尺寸从4×4变成了6×6，使用3×3的卷积核，输出图片尺寸为4×4。

  • 如图（b）所示：填充的大小为2，填充值为0。填充之后，输入图片尺寸从4×4变成了8×8，使用3×3的卷积核，输出图片尺寸为6×6。

 

　　如果在图片高度方向，在第一行之前填充ph1​行，在最后一行之后填充ph2​行；在图片的宽度方向，在第1列之前填充pw1​列，在最后1列之后填充pw2列；则填充之后的图片尺寸为

(H+ph1+ph2)×(W+pw1+pw2)。经过大小为kh×kw的卷积核操作之后，输出图片的尺寸为：

 

　　

 

 

　　在卷积计算过程中，通常会在高度或者宽度的两侧采取等量填充，即ph1=ph2=ph,  pw1=pw2=pw​，上面计算公式也就变为：

　　

 

 

　　此外，卷积核的大小通常使用1，3，5，7这样的奇数。

 

 1.3 步幅

　　最开始的例子是以步幅为1的例子，即每次移动一个像素点，下图为步幅为2的例子，每次移动两个像素点：

　　

 

 

　　当宽和高方向的步幅分别为sh和sw时，输出特征图尺寸的计算公式是：

　　

 

　　

　　假设输入图片尺寸是H×W=100×100，卷积核大小kh×kw=3×3，填充ph=pw=1，步幅为sh=sw=2，则输出特征图的尺寸为：

　　

 

 

1.4 感受野

 　　最后输出的特征的值是原来的输入的像素矩阵通过卷积核的运算的到的，因此输入图像上的每一个点的变化都会引起输出的改变，因此将对应于与卷积核运算的输入数据的方阵区域称之为感受野，以此来感受输入数据的变化。如3×3的卷积核对应于3×3的感受野：

　　

 

　　但是经过更多层卷积过后，感受野的范围会更大，如通过两层3×3的卷积，就会有5×5的感受野：

　　

 

 

1.5 多输入通道、多输出通道和批量操作

　　在实际运用过程中，针对不同的特征，可能通过不同通道来进行处理，所以很多情况是在多通道的条件下进行的。

　　

1.5.1 多输入通道场景

　　在图片当中，其实是有三个维度的，即RGB三个通道，因此这里是需要三个通道进行计算的。要计算卷积的输出结果，卷积核的形式也会发生变化，假设输入图片的通道数为Cin​，

输入数据的形状是Cin×Hin×Win，计算的过程为：

　　

　　过程为：

  1. 对每个通道分别设计一个2维数组作为卷积核，卷积核数组的形状是Cin×kh×kw。

  2. 对任一通道Cin∈[0,Cin)C，分别用大小为kh×kw的卷积核在大小为Hin×Win的二维数组上做卷积。

  3. 将这Cin个通道的计算结果相加，得到的是一个形状为Hout×Wout的二维数组。

 

1.5.2 多输出通道场景

​　　即卷积核也有多个，实现过程为：

　　

 

  1. 对任一输出通道cout∈[0,Cout)，分别使用上面描述的形状为Cin×kh×kw的卷积核对输入图片做卷积。

  2. 将这Cout​个形状为Hout×Wout的二维数组拼接在一起，形成维度为Cout×Hout×Wou​的三维数组。

 

1.5.3 批量操作

　　在卷积神经网络的计算中，通常将多个样本放在一起形成一个mini-batch进行批量操作，通过图示可以很直观的看出来：

　　

 

 

2、卷积算子实例

 2.1简单的黑白边界检测

　　使用Conv2D算子完成一个图像边界检测的任务。图像左边为光亮部分，右边为黑暗部分，需要检测出光亮跟黑暗的分设置宽度方向的卷积核为[1,0,−1]，此卷积核会将宽度方向间隔为1的两个像素点的数值相减。当卷积核在图片上滑动时，如果它所覆盖的像素点位于亮度相同的区域，则左右间隔为1的两个像素点数值的差为0。只有当卷积核覆盖的像素点有的处于光亮区域，有的处在黑暗区域时，左右间隔为1的两个点像素值的差才不为0。将此卷积核作用到图片上，输出特征图上只有对应黑白分界线的地方像素值才不为0界处。

　　代码为：

　　

 1 import matplotlib.pyplot as plt
 2 import numpy as np
 3 import paddle
 4 from paddle.nn import Conv2D
 5 from paddle.nn.initializer import Assign
 6 
 7 # 创建初始化权重参数w
 8 w = np.array([1, 0, -1], dtype='float32')
 9 # 将权重参数调整成维度为[cout, cin, kh, kw]的四维张量
10 w = w.reshape([1, 1, 1, 3])
11 # 创建卷积算子，设置输出通道数，卷积核大小，和初始化权重参数
12 # kernel_size = [1, 3]表示kh = 1, kw=3
13 # 创建卷积算子的时候，通过参数属性weight_attr指定参数初始化方式
14 # 这里的初始化方式时，从numpy.ndarray初始化卷积参数
15 conv = Conv2D(in_channels=1, out_channels=1, kernel_size=[1, 3],
16        weight_attr=paddle.ParamAttr(
17           initializer=Assign(value=w)))
18 
19 # 创建输入图片，图片左边的像素点取值为1，右边的像素点取值为0
20 img = np.ones([50,50], dtype='float32')
21 img[:, 30:] = 0.
22 # 将图片形状调整为[N, C, H, W]的形式
23 x = img.reshape([1,1,50,50])
24 # 将numpy.ndarray转化成paddle中的tensor
25 x = paddle.to_tensor(x)
26 # 使用卷积算子作用在输入图片上
27 y = conv(x)
28 # 将输出tensor转化为numpy.ndarray
29 out = y.numpy()
30 f = plt.subplot(121)
31 f.set_title('input image', fontsize=15)
32 plt.imshow(img, cmap='gray')
33 f = plt.subplot(122)
34 f.set_title('output featuremap', fontsize=15)
35 # 卷积算子Conv2D输出数据形状为[N, C, H, W]形式
36 # 此处N, C=1，输出数据形状为[1, 1, H, W]，是4维数组
37 # 但是画图函数plt.imshow画灰度图时，只接受2维数组
38 # 通过numpy.squeeze函数将大小为1的维度消除
39 plt.imshow(out.squeeze(), cmap='gray')
40 plt.show()

 

　　结果为：

　　

 

 

　　查看卷积层的相关参数和数值：

　　

1 # 查看卷积层的权重参数名字和数值
2 print(conv.weight)
3 # 参看卷积层的偏置参数名字和数值
4 print(conv.bias)

 

　　结果为：

　　

 

 

　　

2.2 图像中物体边缘检测

 　　对于真实的图片，也可以使用合适的卷积核(3*3卷积核的中间值是8，周围一圈的值是8个-1)对其进行操作，用来检测物体的外形轮廓，观察输出特征图跟原图之间的对应关系，如下代码所示：

 　　

 1 import matplotlib.pyplot as plt
 2 from PIL import Image
 3 import numpy as np
 4 import paddle
 5 from paddle.nn import Conv2D
 6 from paddle.nn.initializer import Assign
 7 img = Image.open('./1.png')
 8 
 9 # 设置卷积核参数
10 w = np.array([[-1,-1,-1], [-1,8,-1], [-1,-1,-1]], dtype='float32')/8
11 w = w.reshape([1, 1, 3, 3])
12 # 由于输入通道数是3，将卷积核的形状从[1,1,3,3]调整为[1,3,3,3]
13 w = np.repeat(w, 3, axis=1)
14 # 创建卷积算子，输出通道数为1，卷积核大小为3x3，
15 # 并使用上面的设置好的数值作为卷积核权重的初始化参数
16 conv = Conv2D(in_channels=3, out_channels=1, kernel_size=[3, 3], 
17             weight_attr=paddle.ParamAttr(
18               initializer=Assign(value=w)))
19     
20 # 将读入的图片转化为float32类型的numpy.ndarray
21 x = np.array(img).astype('float32')
22 # 图片读入成ndarry时，形状是[H, W, 3]，
23 # 将通道这一维度调整到最前面
24 x = np.transpose(x, (2,0,1))
25 # 将数据形状调整为[N, C, H, W]格式
26 x = x.reshape(1, 3, img.height, img.width)
27 x = paddle.to_tensor(x)
28 y = conv(x)
29 out = y.numpy()
30 plt.figure(figsize=(20, 10))
31 f = plt.subplot(121)
32 f.set_title('input image', fontsize=15)
33 plt.imshow(img)
34 f = plt.subplot(122)
35 f.set_title('output feature map', fontsize=15)
36 plt.imshow(out.squeeze(), cmap='gray')
37 plt.show()

 

　　结果为：

　　

 

 

2.3 图像均值模糊

 　　另外一种比较常见的卷积核（5*5的卷积核中每个值均为1）是用当前像素跟它邻域内的像素取平均，这样可以使图像上噪声比较大的点变得更平滑，如下代码所示：

 　　

 1 import paddle
 2 import matplotlib.pyplot as plt
 3 from PIL import Image
 4 import numpy as np
 5 from paddle.nn import Conv2D
 6 from paddle.nn.initializer import Assign
 7 # 读入图片并转成numpy.ndarray
 8 # 换成灰度图
 9 img = Image.open('./test.jpg').convert('L')
10 img = np.array(img)
11 
12 # 创建初始化参数
13 w = np.ones([1, 1, 5, 5], dtype = 'float32')/25
14 conv = Conv2D(in_channels=1, out_channels=1, kernel_size=[5, 5], 
15         weight_attr=paddle.ParamAttr(
16          initializer=Assign(value=w)))
17 x = img.astype('float32')
18 x = x.reshape(1,1,img.shape[0], img.shape[1])
19 x = paddle.to_tensor(x)
20 y = conv(x)
21 out = y.numpy()
22 
23 plt.figure(figsize=(20, 12))
24 f = plt.subplot(121)
25 f.set_title('input image')
26 plt.imshow(img, cmap='gray')
27 
28 f = plt.subplot(122)
29 f.set_title('output feature map')
30 out = out.squeeze()
31 plt.imshow(out, cmap='gray')
32 
33 plt.show()

 

 　　结果为：

　　

 

3、池化

　　池化是使用某一位置的相邻输出的总体统计特征代替网络在该位置的输出，其好处是当输入数据做出少量平移时，经过池化函数后的大多数输出还能保持不变。比如：当识别一张图像是否是人脸时，我们需要知道人脸左边有一只眼睛，右边也有一只眼睛，而不需要知道眼睛的精确位置，这时候通过池化某一片区域的像素点来得到总体统计特征会显得很有用。由于池化之后特征图会变得更小，如果后面连接的是全连接层，能有效的减小神经元的个数，节省存储空间并提高计算效率。

　　

 

3.1 平均池化

 　　（a）：平均池化。这里使用大小为2×22\times22×2的池化窗口，每次移动的步幅为2，对池化窗口覆盖区域内的像素取平均值，得到相应的输出特征图的像素值。

3.2 最大池化

　　（b）：最大池化。对池化窗口覆盖区域内的像素取最大值，得到输出特征图的像素值。当池化窗口在图片上滑动时，会得到整张输出特征图。池化窗口的大小称为池化大小，用kh×kw表示。在卷积神经网络中用的比较多的是窗口大小为2×2，步幅为2的池化。

　　

　　与卷积核类似，池化窗口在图片上滑动时，每次移动的步长称为步幅，当宽和高方向的移动大小不一样时，分别用sw​和sh​表示。也可以对需要进行池化的图片进行填充，填充方式与卷积类似，假设在第一行之前填充ph1​行，在最后一行后面填充ph2​行。在第一列之前填充pw1列，在最后一列之后填充pw2​列，则池化层的输出特征图大小为：

 

　　

 

　　在卷积神经网络中，通常使用2×2大小的池化窗口，步幅也使用2，填充为0，则输出特征图的尺寸为：

　　

 

　

4、批归一化

 　　目的是对神经网络中间层的输出进行标准化处理，使得中间层的输出更加稳定。对于深度神经网络来说，由于参数是不断更新的，即使输入数据已经做过标准化处理，但是对于比较靠后的那些层，其接收到的输入仍然是剧烈变化的，通常会导致数值不稳定，模型很难收敛。BatchNorm能够使神经网络中间层的输出变得更加稳定，并有如下三个优点：

　　

  • 使学习快速进行（能够使用较大的学习率）

  • 降低模型对初始值的敏感性

  • 从一定程度上抑制过拟合

　　

　　其主要思路是在训练时以mini-batch为单位，对神经元的数值进行归一化，使数据的分布满足均值为0，方差为1。具体计算过程如下：

　　①：计算mini-batch内样本的均值，其中x^(i)表示mini-batch中的第i个样本。：

　　

 

　　②：计算mini-batch内样本的方差：

　　　

 

 

　　先计算一个批次内样本的均值和方差，然后再对输入数据做归一化，将其调整成均值为0，方差为1的分布。

 

　　③：计算标准化后的输出，其中ϵ是一个微小值，其主要作用是为了防止分母为0。：

　　

 

　　示例1：当输入数据形状是[N,K]时，一般对应全连接层的输出，示例代码如下所示。

　　

 1 # 输入数据形状是 [N, K]时的示例
 2 import numpy as np
 3 import paddle
 4 from paddle.nn import BatchNorm1D
 5 # 创建数据
 6 data = np.array([[1,2,3], [4,5,6], [7,8,9]]).astype('float32')
 7 # 使用BatchNorm1D计算归一化的输出
 8 # 输入数据维度[N, K]，num_features等于K
 9 bn = BatchNorm1D(num_features=3)    
10 x = paddle.to_tensor(data)
11 y = bn(x)
12 print('output of BatchNorm1D Layer: \n {}'.format(y.numpy()))
13 
14 # 使用Numpy计算均值、方差和归一化的输出
15 # 这里对第0个特征进行验证
16 a = np.array([1,4,7])
17 a_mean = a.mean()
18 a_std = a.std()
19 b = (a - a_mean) / a_std
20 print('std {}, mean {}, \n output {}'.format(a_mean, a_std, b))

 

　　结果为：

　　

 

 

　　示例2： 当输入数据形状是[N,C,H,W]时， 一般对应卷积层的输出，示例代码如下所示：

　　

 1 # 输入数据形状是[N, C, H, W]时的batchnorm示例
 2 import numpy as np
 3 import paddle
 4 from paddle.nn import BatchNorm2D
 5 
 6 # 设置随机数种子，这样可以保证每次运行结果一致
 7 np.random.seed(100)
 8 # 创建数据
 9 data = np.random.rand(2,3,3,3).astype('float32')
10 # 使用BatchNorm2D计算归一化的输出
11 # 输入数据维度[N, C, H, W]，num_features等于C
12 bn = BatchNorm2D(num_features=3)
13 x = paddle.to_tensor(data)
14 y = bn(x)
15 print('input of BatchNorm2D Layer: \n {}'.format(x.numpy()))
16 print('output of BatchNorm2D Layer: \n {}'.format(y.numpy()))
17 
18 # 取出data中第0通道的数据，
19 # 使用numpy计算均值、方差及归一化的输出
20 a = data[:, 0, :, :]
21 a_mean = a.mean()
22 a_std = a.std()
23 b = (a - a_mean) / a_std
24 print('channel 0 of input data: \n {}'.format(a))
25 print('std {}, mean {}, \n output: \n {}'.format(a_mean, a_std, b))
26 
27 # 提示：这里通过numpy计算出来的输出
28 # 与BatchNorm2D算子的结果略有差别，
29 # 因为在BatchNorm2D算子为了保证数值的稳定性，
30 # 在分母里面加上了一个比较小的浮点数epsilon=1e-05

　　结果为：

　　

 

 

5、丢弃法

　　深度学习中一种常用的抑制过拟合的方法，其做法是在神经网络学习过程中，随机删除一部分神经元。训练时，随机选出一部分神经元，将其输出设置为0，这些神经元将不对外传递信号。应用Dropout之后，会将标了×\times×的神经元从网络中删除，让它们不向后面的层传递信号。在学习过程中，丢弃哪些神经元是随机决定，因此模型不会过度依赖某些神经元，能一定程度上抑制过拟合。

　　

 

 

　　但是在使用Dropout的神经网络中，会存在因为随机删除神经元导致最后的预测值偏小，同时因为在预测的时候不会删除数据，导致训练时的和预测时的会不一致，基于这两个问题，飞桨提出了两个解决方法：

　　①：downscale_in_infer：训练时以比例r随机丢弃一部分神经元，不向后传递它们的信号；预测时向后传递所有神经元的信号，但是将每个神经元上的数值乘以 (1−r)。

 

　　②：upscale_in_train：训练时以比例r随机丢弃一部分神经元，不向后传递它们的信号，但是将那些被保留的神经元上的数值除以 (1−r)；预测时向后传递所有神经元的信号，不做任何处理。

 

　　

　　在飞桨Dropout API中，通过mode参数来指定用哪种方式对神经元进行操作，

　　paddle.nn.Dropout(p=0.5, axis=None, mode="upscale_in_train”, name=None)

　　主要参数如下：

  • p (float) ：将输入节点置为0的概率，即丢弃概率，默认值：0.5。该参数对元素的丢弃概率是针对于每一个元素而言，而不是对所有的元素而言。举例说，假设矩阵内有12个数字，经过概率为0.5的dropout未必一定有6个零。

  • mode(str) ：丢弃法的实现方式，有'downscale_in_infer'和'upscale_in_train'两种，默认是'upscale_in_train'。

 

　　实例：

　　

 1 # dropout操作
 2 import paddle
 3 import numpy as np
 4 
 5 # 设置随机数种子，这样可以保证每次运行结果一致
 6 np.random.seed(100)
 7 # 创建数据[N, C, H, W]，一般对应卷积层的输出
 8 data1 = np.random.rand(2,3,3,3).astype('float32')
 9 # 创建数据[N, K]，一般对应全连接层的输出
10 data2 = np.arange(1,13).reshape([-1, 3]).astype('float32')
11 # 使用dropout作用在输入数据上
12 x1 = paddle.to_tensor(data1)
13 # downgrade_in_infer模式下
14 drop11 = paddle.nn.Dropout(p = 0.5, mode = 'downscale_in_infer')
15 droped_train11 = drop11(x1)
16 # 切换到eval模式。在动态图模式下，使用eval（）切换到求值模式，该模式禁用了dropout。
17 drop11.eval()
18 droped_eval11 = drop11(x1)
19 # upscale_in_train模式下
20 drop12 = paddle.nn.Dropout(p = 0.5, mode = 'upscale_in_train')
21 droped_train12 = drop12(x1)
22 # 切换到eval模式
23 drop12.eval()
24 droped_eval12 = drop12(x1)
25 
26 x2 = paddle.to_tensor(data2)
27 drop21 = paddle.nn.Dropout(p = 0.5, mode = 'downscale_in_infer')
28 droped_train21 = drop21(x2)
29 # 切换到eval模式
30 drop21.eval()
31 droped_eval21 = drop21(x2)
32 drop22 = paddle.nn.Dropout(p = 0.5, mode = 'upscale_in_train')
33 droped_train22 = drop22(x2)
34 # 切换到eval模式
35 drop22.eval()
36 droped_eval22 = drop22(x2)
37     
38 print('x1 {}, \n droped_train11 \n {}, \n droped_eval11 \n {}'.format(data1, droped_train11.numpy(),  droped_eval11.numpy()))
39 print('x1 {}, \n droped_train12 \n {}, \n droped_eval12 \n {}'.format(data1, droped_train12.numpy(),  droped_eval12.numpy()))
40 print('x2 {}, \n droped_train21 \n {}, \n droped_eval21 \n {}'.format(data2, droped_train21.numpy(),  droped_eval21.numpy()))
41 print('x2 {}, \n droped_train22 \n {}, \n droped_eval22 \n {}'.format(data2, droped_train22.numpy(),  droped_eval22.numpy()))

 

　　结果为：

　　

 

 

6、总结

　　通过对卷积神经的基础知识进一步的学习，对其基础概念以及相关API的运用以处理前向计算与后向计算的错误的处理，此外对飞桨API的了解也更加深刻。但是对于其中的很多细节很大程度上是一知半解的。

 

 

7、参考资料

卷积神经网络基础：https://aistudio.baidu.com/aistudio/projectdetail/4407490 

图像边缘处理：https://aistudio.baidu.com/aistudio/projectdetail/2064017?channelType=0&channel=0

posted @ 2022-08-08 22:14  I'MPGB  阅读(64)  评论(0)  编辑  收藏  举报