Deep Learning-深度学习（一）

深度学习入门

1、人工智能、机器学习、深度学习

1.1 人工智能（AI）

　　一个比较宽泛的概念。即用来模拟人的智能的理论，并对这个模拟出来的智能进行延伸和开拓。通俗来讲就是要达到用机器模拟人类的聪慧来处理更加复杂的事情这一目的的一个集理论知识和技术、系统的一门学科。发展到现在分支众多、仍旧是较为笼统的。更多的是停留在一个以目的为框架的这样一个位置。

 

1.2 机器学习（ML）　

　　是能够对人工智能理论一个较为有效的实现的一个方向。是人工智能的核心，研究计算机如何模拟以及实现人的学习行为，能够获得新的知识以及技能，并能够进行自身的不断更新、知识重构、自我完善的功能。

　　其实现分为两步：训练和预测。训练（归纳），就是和人一样，能够在日常生活中获得一般的、普遍的规律。在计算机学习中，要归纳得出抽象的规律是通过一定量的数据样本的处理才能得到的，值得注意的是这个样本是需要同时具有输入X与对应输出Y，这样的数据对（模型对）才能够让及其学习其中X与Y之间对应的关系的。预测（演绎），在训练的基础上能够得到的规律对之后的未知输入X进行对应的输出Y的一个预测。当对应的预测得出的Y是与真实情况相一致的，那么则可以认为该模型是有效的。

　　通过分析，可以发现机器学习过程中确定模型的三个关键要素为：假设、评价、优化。即对数据的处理，对规律进行假设，评价其是否具有有效性，以及对模型进行优化，使得模型更加具有有效性。

 

1.3 深度学习（DL）

　　是在机器学习中的又一个分支，同于传统的机器学习，深度学习的理论结构为模型假设、评价函数和优化算法，但他们的根本差别在于假设的复杂度。其中最为吸引人的眼球的点就是神经网络概念。

　　神经网络，在学习的时候有一个机器对照片进行读取的例子，因为机器是将信息数据化，而无法像人一样能够进行像素的直接识别。而像素到具体对应的数字信息这个过程是需要很多的数据转化，而且对于不同的像素，转化方式是不同的。因此为了解决这个问题，于是对应不同的神经元能够通过不同的组织来实现不同器官神经系统的专一化的特点，提出神经网络的概念，能够对复杂信息进行有效处理。神经网络的基本结构如下：

 

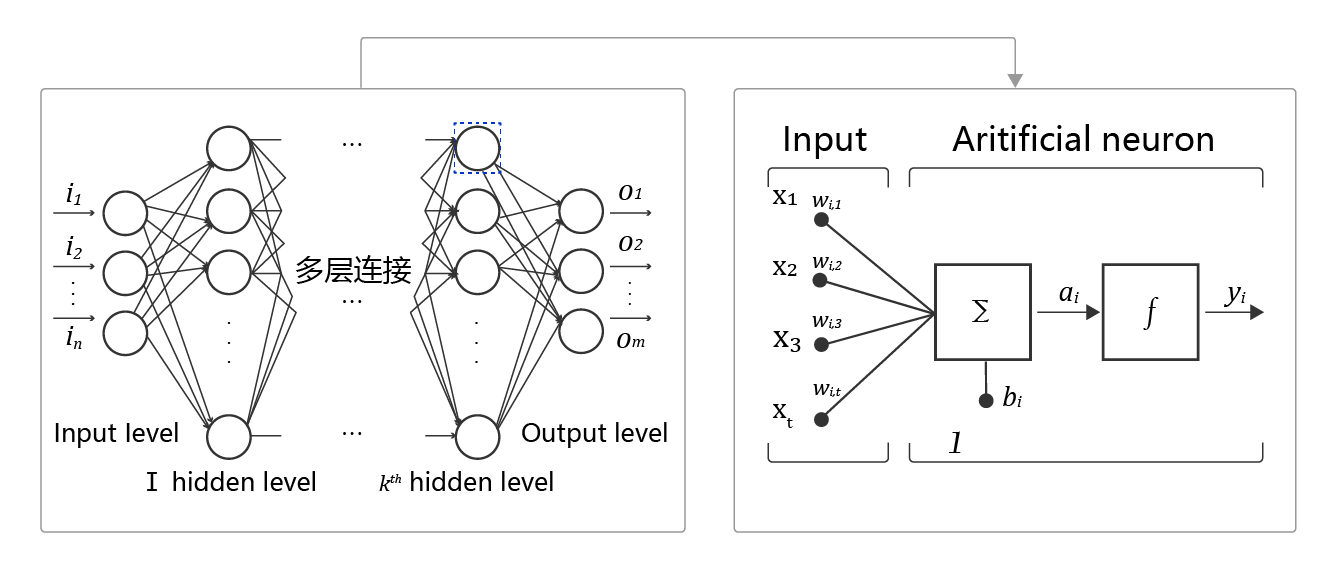
　　其中主要的概念有：①神经元，即神经网络中的每个节点，我理解其为构成最终输出的未处理原始数据的一个元素，是它所对应的信息板块数据的加权和以及激活函数构成，即对这一板块的数据的单独处理。②多层连接，即各种要素都汇聚在一起，也即是大量的神经元按照不同的方式排布，构成最终的神经网络，即完成这一个“器官”的功能。③前向计算，即从数据的输入到最后得到输出的这样一个过程。④计算图。展示计算逻辑的图。其中的计算逻辑即对很多参数进行不同函数进行处理：Y=f3​(f2​(f1​(w1​⋅x1​+w2​⋅x2​+w3​⋅x3​+b)+…)…)…)。

 

 

1.4 三者之间的关系

　　

 

 

2、深度学习环境的搭建

　　这里可以通过两种方式进行安装，即CPU的paddlepaddle安装以及GPU的paddlepaddle安装，以越高级越好的原则，这里选择安装GPU的paddlepaddle安装。

　　首先既然是要利用pip()命令进行安装，那么首先需要安装python这里需要3.6/3.7/3.8/3.9/3.10版本，下载地址为：Download Python | Python.org。同时pip 版本 20.2.2或更高版本 (64 bit)。

　　其次要查看自己电脑是否有GPU，查看方式为任务管理器->性能，如果有GPU即可。此外查看GPU的算力是否在3.5以上（查到GPU版本，对照算力表即可)，接着对应相关版本的CUDA工具包和其cuDNN补丁进行安装和下载。这里推荐使用CUDA10.2版本。具体版本和对应的cuDNN补丁表为：

  • CUDA 工具包10.1/10.2 配合 cuDNN v7.6.5

  • CUDA 工具包 11.0 配合 cuDNN v8.0.2

  • CUDA 工具包 11.1 配合 cuDNN v8.1.1

  • CUDA 工具包 11.2 配合 cuDNN v8.2.1

　　对应的下载地址，CUDA 工具包：CUDA Toolkit Archive | NVIDIA Developer。 cuDNN：https://developer.nvidia.com/rdp/cudnn-download。

　　成功安装后，再在命令行利用pip命令进行paddlepaddle的安装，其对应版本的命令为：

　　CUDA10.1的PaddlePaddle

　　python -m pip install paddlepaddle-gpu==2.3.0.post101 -f https://www.paddlepaddle.org.cn/whl/windows/mkl/avx/stable.html

　　CUDA10.2的PaddlePaddle

　　python -m pip install paddlepaddle-gpu==2.3.0 -i https://mirror.baidu.com/pypi/simple

　　CUDA11.0的PaddlePaddle

　　python -m pip install paddlepaddle-gpu==2.3.0.post110 -f https://www.paddlepaddle.org.cn/whl/windows/mkl/avx/stable.html

　　CUDA11.1的PaddlePaddle

　　python -m pip install paddlepaddle-gpu==2.3.0.post111 -f https://www.paddlepaddle.org.cn/whl/windows/mkl/avx/stable.html

　　最后，在python中进行安装的验证，进入python解释器，输入import paddle ，再输入 paddle.utils.run_check()。如果出现PaddlePaddle is installed successfully!说明已成功安装。即如下图所示：

　　　　

 

3、波士顿房价预测实战

　　3.1数据处理

　　①导入数据集：读取数据集中的内容到磁盘，同时定义影响房价的十三个因素以及一个房价属性。

　　

1     # 读取以空格分开的文件，变成一个连续的数组
2     firstdata = np.fromfile('housing.data', sep=' ')
3     # 添加属性
4     feature_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT',
5                      'MEDV']
6     # 列的长度
7     feature_num = len(feature_names)
8     # print(firstdata.shape)  输出结果:(7084, )

 

　　②对数据集进行划分：因为每14个数是一组的，对应着输入输出关系，因此要将磁盘中的一维数组进行整理。

1     # 构造506*14的二维数组
2     data = firstdata.reshape([firstdata.shape[0] // feature_num, feature_num])

　　

　　③规定以80%的数据进行学习，以及20%的数据进行测试。

1     # 将原数据集拆分成训练集和测试集
2     # 这里使用80%的数据做训练，20%的数据做测试
3     # 测试集和训练集必须是没有交集的
4     ratio=0.8
5     offset=int(data.shape[0]*ratio)
6     # print(offset)
7     training_data=data[:offset]#训练的数据百分之80的数据集

 

　　④对每一列的数据进行归一化，使其值在0-1之间。

 1     # axis=0表示列
 2     # axis=1表示行
 3     maximums, minimums, avgs = \
 4                          training_data.max(axis=0), \
 5                          training_data.min(axis=0), \
 6          training_data.sum(axis=0) / training_data.shape[0]
 7     # 对所有数据进行归一化处理
 8     for i in range(feature_num):
 9         # print(maximums[i], minimums[i], avgs[i])
10         # 归一化，减去平均值是为了移除共同部分，凸显个体差异
11         data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i])
12 
13     # 覆盖上面的训练集
14     training_data = data[:offset]
15     # 剩下的20%为测试集
16     test_data = data[offset:]

 

 　　3.2模型设计

　　①利用随机数进行最初始的一个权重值，此时的权重是不准确的，要随着不断的学习方能够不断接近各个因素的正确权重值。线性回归的完整输出为z=t+b，因此需要初始一个b.

 

1  　　def __init__(self, num_of_weights):
2         # 随即产生w的初始值
3         # seed(0)表示设置了随机种子，保证程序每次运行结果的一致性
4         np.random.seed(0)
5         # self.w的结构为num_of_weights行，1列
6         self.w = np.random.randn(num_of_weights, 1)
7         # b初始化为0
8         self.b = 0.

 

　　②将各个因素与其对应权重值进行点乘，加b，得到最终输出。

1     　def forward(self, x):
2         # dot()功能：向量点积和矩阵乘法
3         # 根据下面x的取值可以确定x和z的结构
4         z = np.dot(x, self.w) + self.b
5         return z

 

　　3.3训练配置

　　通过计算得出的房价z与实际的房价之间是有一定的差距的，因此这里对于回归问题，常采用的衡量方法是使用均方误差作为评价模型好坏的指标，具体定义为：

　　

　　其中Loss为衡量模型好坏的标准，同时，因为计算损失函数时需要把每个样本的损失函数值都考虑到，所以我们需要对单个样本的损失函数进行求和，并除以样本总数N。

　　

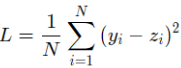
　　具体实现为：

 1　　　　def loss(self, z, y):
 2         # 根据下面y的取值可以确定y的结构
 3         error = z - y
 4         # num_samples为总行数404
 5         num_samples = error.shape[0]
 6         # cost为均方误差，用来评价模型的好坏
 7         cost = error * error
 8         # 计算损失时需要把每个样本的损失都考虑到
 9         # 对单个样本的损失函数进行求和，并除以样本总数
10         cost = np.sum(cost) / num_samples
11         return cost

 

　　3.4训练过程

　　该过程即是求权重值w和值b的过程，训练过程是深度学习模型的关键要素之一，其目标是让定义的损失函数Loss尽可能的小，也就是说找到一个参数解w和b，使得损失函数取得极小值。让损失函数取极小值的w和b应该是下述方程组的解：

　　　　

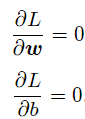
　　其中L表示的是损失函数的值，w为模型权重，b为偏置项。w和b均为要学习的模型参数。

　　其中对于损失函数进行矩阵化表示：

　　

　　其中y为N个样本的标签值构成的列向量；X为N个样本特征向量构成的矩阵。该公式对b的偏导数为：

　　

　　令它为0，可得到关于b的式子：

　　

　 　

　   

　　再利用求出的b对L进行对w求偏导，为：

　　

　　同样的，令其等于0，可得最优参数：

　　

 

　　

 

 

 　　对于线性回归式的问题来说，对于以上模型，通过输入样本数据(x,y)就可以了。但是在非线性回归的问题中，则需要引入更加普适的数值求解方法：梯度下降法。

　　关键是找到一组(w,b)，使得损失函数L取极小值。我们先看一下损失函数L只随两个参数w5，w9​变化时的简单情形，启发下寻解的思路。

　　

 

　　这里所取的这两个参数是任意的，因为只是为了画出三维图，能够更好的直观感受坡度的下降过程而已。如果参数过多，那么无法画出n维图。

　　这里可以对这个三维图进行画出，以便更好理解，但是这里不属于整个模型预测中的代码的一部分。

 1 net = Network(13)
 2 losses = []
 3 #只画出参数w5和w9在区间[-160, 160]的曲线部分，以及包含损失函数的极值
 4 w5 = np.arange(-160.0, 160.0, 1.0)
 5 w9 = np.arange(-160.0, 160.0, 1.0)
 6 losses = np.zeros([len(w5), len(w9)])
 7 
 8 #计算设定区域内每个参数取值所对应的Loss
 9 for i in range(len(w5)):
10     for j in range(len(w9)):
11         net.w[5] = w5[i]
12         net.w[9] = w9[j]
13         z = net.forward(x)
14         loss = net.loss(z, y)
15         losses[i, j] = loss
16 
17 #使用matplotlib将两个变量和对应的Loss作3D图
18 import matplotlib.pyplot as plt
19 from mpl_toolkits.mplot3d import Axes3D
20 fig = plt.figure()
21 ax = Axes3D(fig)
22 
23 w5, w9 = np.meshgrid(w5, w9)
24 
25 ax.plot_surface(w5, w9, losses, rstride=1, cstride=1, cmap='rainbow')
26 plt.show()
27 <Figure size 640x480 with 1 Axes>

 

　　能够得到如下所示的图，可以看出的确是一个山谷型图像。

　　　

 

　　这种方法的最终目的是为了选择出最好的参数组，使得最后梯度值为0，其步骤为：①随机的选一组初始值，例如：[w5,w9] = [−100.0,−100.0]，②选取下一个点[w5′,w9′]，使得L(w5′,w9′)<L(w5,w9)，③重复步骤2，直到损失函数几乎不再下降。其中最为重要的有两点，第一要保证LLL是下降的，第二要使得下降的趋势尽可能的快。

　　对于梯度的计算有，首先定义损失函数，这里为了能够简化式子，因此添加了一个因子1/2：

　　

 

　　表示预测值：

　　

 

　　梯度的定义为：

　　

 

　　可以计算出损失函数对w,b的偏导：

　　

 

　　

 

　　以上为对所有样本进行分析的过程，其代码实现为：

　　①：前向计算，即计算预测输出，计算损失：

 1     def loss(self, z, y):
 2         # 根据下面y的取值可以确定y的结构
 3         error = z - y
 4         # num_samples为总行数404
 5         num_samples = error.shape[0]
 6         # cost为均方误差，用来评价模型的好坏
 7         cost = error * error
 8         # 计算损失时需要把每个样本的损失都考虑到
 9         # 对单个样本的损失函数进行求和，并除以样本总数
10         cost = np.sum(cost) / num_samples
11         return cost

　　②计算w和b的梯度：

 1     def gradient(self, x, y):
 2         # 调用forward函数，得到z
 3         z = self.forward(x)
 4         # 计算w梯度，得到一个13维向量，每个分量分别代表该维度的梯度
 5         gradient_w = (z - y) * x
 6         # 均值函数mean：求均值
 7         # axis 不设置值，对 m*n 个数求均值，返回一个实数
 8         # axis = 0：压缩行，对各列求均值，返回 1* n 矩阵
 9         # axis =1 ：压缩列，对各行求均值，返回 m *1 矩阵
10         gradient_w = np.mean(gradient_w, axis=0)
11         # 增加维度，变成 n * 1 的矩阵
12         gradient_w = gradient_w[:, np.newaxis]
13         # 计算b的梯度
14         gradient_b = (z - y)
15         # b为一个数值，不需要再增加维度
16         gradient_b = np.mean(gradient_b)
17         return gradient_w, gradient_b

　　③更新梯度：

1     # 确定损失函数更小的点
2     # 更新梯度
3     def update(self, gradient_w, gradient_b, eta=0.01):
4         # 更新参数
5         # 相减：参数需要向梯度的反方向移动。
6         # eta：控制每次参数值沿着梯度反方向变动的大小，即每次移动的步长，又称为学习率。
7         self.w = self.w - eta * gradient_w
8         self.b = self.b - eta * gradient_b

　　④以0.01的幅度进行在梯度上的移动，即控制每次参数值沿着梯度反方向变动的大小，即每次移动的步长，又称为学习率。此外这里还进行了归一化。迭代次数初始设置为100.

 1     # 迭代100次，每次移动0.01
 2     def train(self, x, y, iterations=100, eta=0.01):
 3         losses = []
 4         for i in range(iterations):
 5             z = self.forward(x)
 6             L = self.loss(z, y)
 7             gradient_w, gradient_b = self.gradient(x, y)
 8             self.update(gradient_w, gradient_b, eta)
 9             losses.append(L)
10             # 循环输出i末尾为9，间隔为10的数据
11             if (i + 1) % 10 == 0:
12                 print('iter {}, loss{}'.format(i, L))
13         return losses

　　⑤最终进行整个学习过程的运行，即获取数据、创建网络、启动训练、画出损失函数的变化趋势。

 1 # 获取数据
 2 training_data, test_data = load_data()
 3 # 取训练集全部行的前13列
 4 x = training_data[:, :-1]
 5 # 取训练集全部行的最后一列
 6 y = training_data[:, -1:]
 7 # 创建网络
 8 net = Network(13)
 9 num_iterations = 1000
10 # 启动训练，迭代次数为1000，步长为0.01
11 losses = net.train(x, y, iterations=num_iterations, eta=0.01)
12 
13 # 画出损失函数的变化趋势
14 plot_x = np.arange(num_iterations)
15 plot_y = np.array(losses)
16 plt.plot(plot_x, plot_y)
17 plt.show()

 

　　3.5实战结果

　　①损失函数随着不断地学习（体现在迭代次数上），函数值的变化，

　

 

　　②损失函数变化趋势图：

　　

 

 

4、总结

　　以上就是在第一阶段所学的知识，对深度学习的基本概念，对应的公式推导，以及代码复现有了比较紧密联系的认识。该模型还需要进一步优化，在接下来的学习过程中会不断提高自己的能力。

 

5、参考资料

paddlepaddle安装：https://www.paddlepaddle.org.cn/documentation/docs/zh/install/pip/windows-pip.html#muqianfeijiangzhichidehuanjing

CUDA安装：https://blog.csdn.net/weixin_43848614/article/details/117221384

数据集下载：https://aistudio.baidu.com/aistudio/datasetdetail/64

更加详细教程（含源代码）：https://aistudio.baidu.com/aistudio/projectdetail/4287981

posted @ 2022-07-04 13:44  I'MPGB  阅读(229)  评论(0)  编辑  收藏  举报