[ AHOI 2017 / HNOI 2017 ] 抛硬币

题目

Luogu
LOJ
Acwing

思路

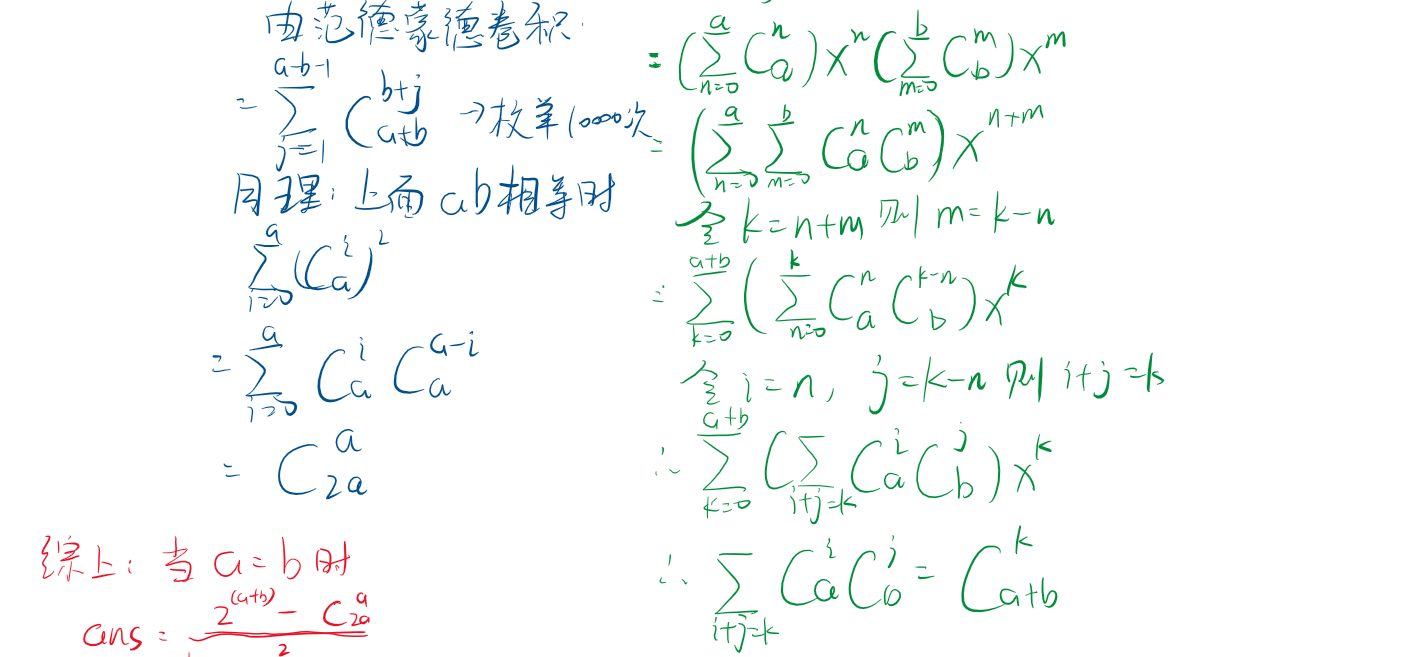
代码

#include <iostream>
#include <algorithm>
#define int long long
using namespace std;
int qmi(int a, int b, int mod) {
    int res = 1 % mod;
    for (; b; b >>= 1, a = a * a % mod)
        if (b & 1) res = res * a % mod;
    return res;
}
void EX_GCD(int a, int b, int &x, int &y) {
    if (!b) return x = 1, y = 0, (void)0;
    EX_GCD(b, a % b, y, x), y -= a / b * x;
}
int inv(int a, int b) {
    int x, y; EX_GCD(a, b, x, y);
    return (x + b) % b;
}
int FT[2][1953200], a, b, k, nb[15];
int lucas(int n, int p, int mod) {
    if (n == 0) return 1;
    int *f = FT[p != 2];
    return lucas(n / p, p, mod) * 
           f[n % mod] % mod * 
           // 0 ~ mod - 1
           qmi(f[mod - 1], n / mod, mod) % mod;
}
int calc(int n, int m, int p, int mod) {
    int d = 0;
    for (int i = n; i; i /= p) d += i / p;
    for (int i = m; i; i /= p) d -= i / p;
    for (int i = n - m; i; i /= p) d -= i / p;
    // 因子次数大于九的时候, 直接返回 0 即可
    // 不加此优化会 TLE
    if (d >= 9) return 0; 
    int p1 = lucas(n, p, mod), 
        p2 = lucas(m, p, mod), 
        p3 = lucas(n - m, p, mod); 
    return qmi(p, d, mod) * 
           p1 % mod * 
           inv(p2, mod) % mod *
           inv(p3, mod) % mod;
}

void init(int p, int mod) {
    int *f = FT[p != 2];
    f[0] = 1;
    for (int i = 1; i < mod; i++)
        f[i] = (i % p) ? i * f[i - 1] % mod : f[i - 1];
}
// 为了方便, 模数设为 1e9, 之后根据具体 k 求即可
// 所有质因子乘起来是 1e9
const int MAX = 1e9;
int CRT(int a, int b) { return a * (MAX / b) % MAX * inv(MAX / b, b) % MAX; }
int C(int a, int b) {
    int c2 = 512, c5 = 1953125;
    int x = calc(a, b, 2, c2), y = calc(a, b, 5, c5);
    return (CRT(x, c2) + CRT(y, c5)) % MAX;
}
void prit(int x) {
    int t = x, bit = 0, s = 1;
    while (t) t /= 10, bit++;
    for (int i = 0; i < k - bit; i++) cout << "0";
    while (k--) s *= 10;
    cout << x % s << endl;
}
signed main() {
    init(2, 512), init(5, 1953125);
    while (cin >> a >> b >> k)
        if (a == b) prit((qmi(2, a + b - 1, MAX) - C(2 * a - 1, a) + MAX) % MAX);
        else {
            int res = qmi(2, a + b - 1, MAX);
            for (int i = 1; i <= (a - b - 1) / 2; i++)
                res = (res + C(a + b, b + i)) % MAX;
            if (!((a + b) % 2)) res = (res + C(a + b - 1, (a + b) / 2)) % MAX;
            prit(res);
        }
    return 0;
}