[ AGC005 F ] Many Easy Problems

题目

Atcoder

思路

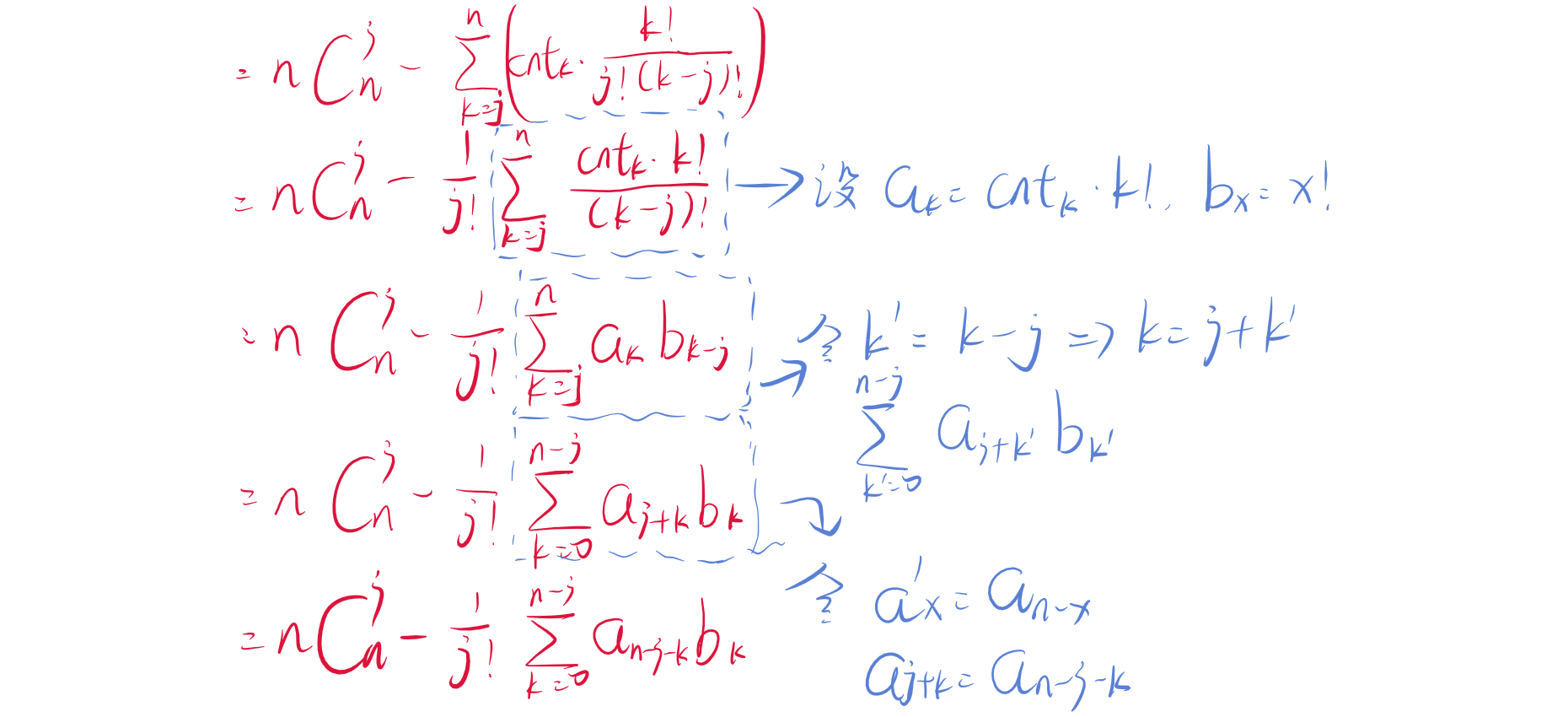
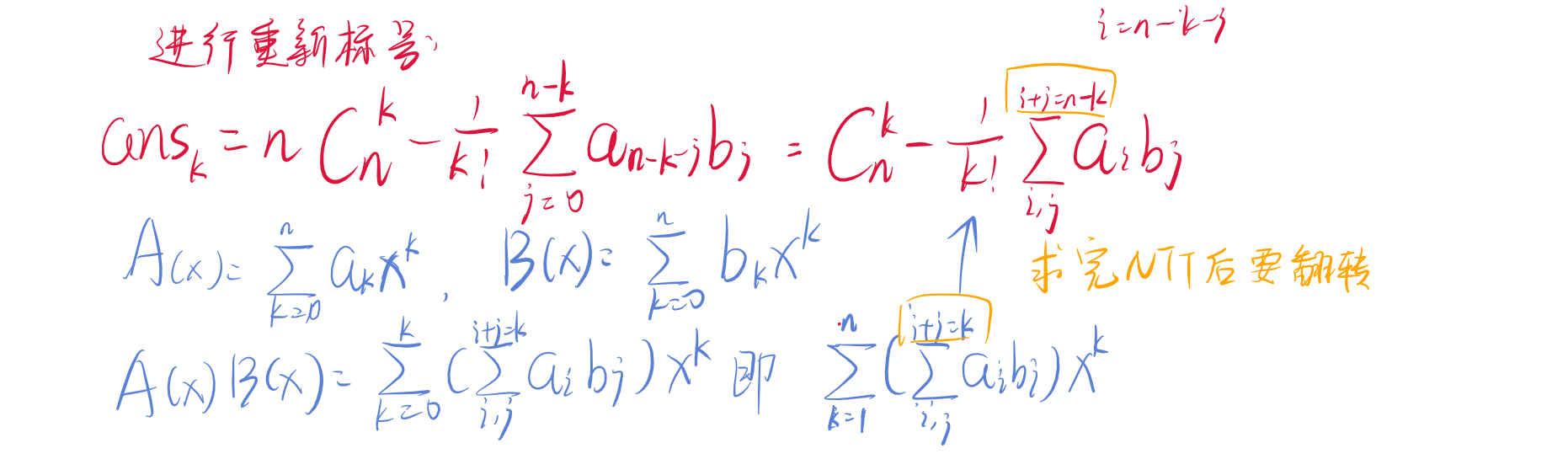
代码

#include <iostream>
#include <cstring>
#include <algorithm>
#define int long long
using namespace std;
const int N = 1000010, p = 924844033, g = 5; // 注意原根是 5
int n, cnt[N], sz[N];
int h[N], val[N], ptr[N], idx;
int fact[N], invf[N];
int A[N], B[N];
void add(int a, int b) { val[idx] = b, ptr[idx] = h[a], h[a] = idx++; }
int qmi(int a, int b) {
    int res = 1 % p;
    for (; b; b >>= 1, a = a * a % p) 
        if (b & 1) res = res * a % p;
    return res;
}
int s = 0, a = 0;
void DFS_init(int u, int fa) {
    sz[u] = 1;
    for (int i = h[u], v = val[i]; i != -1; i = ptr[i], v = val[i]) 
        if (v != fa) DFS_init(v, u), sz[u] += sz[v], cnt[sz[v]]++;
    cnt[n - sz[u]]++;
}
int rev[N], tot, bit;
void NTT(int A[], int sign) {
    for (int i = 0; i < tot; i++)
        if (i < rev[i]) swap(A[i], A[rev[i]]);
    for (int mid = 1; mid < tot; mid <<= 1) {
        int w1 = qmi(g, (p - 1) / (mid * 2));
        if (sign == -1) w1 = qmi(w1, p - 2);
        for (int i = 0; i < tot; i += (mid << 1))
            for (int j = 0, wk = 1; j < mid; j++, wk = wk * w1 % p) {
                int x = A[i + j], y = wk * A[i + j + mid] % p;
                A[i + j] = (x + y) % p, A[i + j + mid] = ((x - y) % p + p) % p;
            }
    }
}
void NTT(int A[], int B[]) {
    while ((1 << bit) < (n + n + 1)) bit++;
    tot = 1 << bit;
    for (int i = 0; i < tot; i++) 
        rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
    NTT(A, 1), NTT(B, 1);
    for (int i = 0; i < tot; i++) A[i] = A[i] * B[i] % p;
    NTT(A, -1);
    int k = qmi(tot, p - 2);
    for (int i = 0; i < tot; i++) 
        A[i] = A[i] * k % p;
}
signed main() {
    cin >> n;
    memset(h, -1, sizeof h);
    for (int i = 1, a, b; i < n; i++)
        cin >> a >> b, add(a, b), add(b, a);
    DFS_init(1, 0);
    fact[0] = invf[0] = 1;
    for (int i = 1; i <= n; i++) 
        fact[i] = fact[i - 1] * i % p, 
        invf[i] = qmi(fact[i], p - 2);
    cnt[0] = 0; // 根节点的时候, cnt[n - sz[u]] 即 cnt[0];
    for (int i = 0; i <= n; i++) 
        A[i] = cnt[i] * fact[i] % p,
        B[i] = invf[i];
    reverse(A, A + n + 1);
    NTT(A, B);
    reverse(A, A + n + 1);
    for (int i = 1; i <= n; i++)
        cout << ((n * fact[n] % p * invf[i] % p * invf[n - i] % p 
                - invf[i] * A[i] % p) % p + p) % p << endl;
    return 0;
}