[ SCOI 2016 ] 围棋

题目

Luogu
LOJ
Acwing

思路

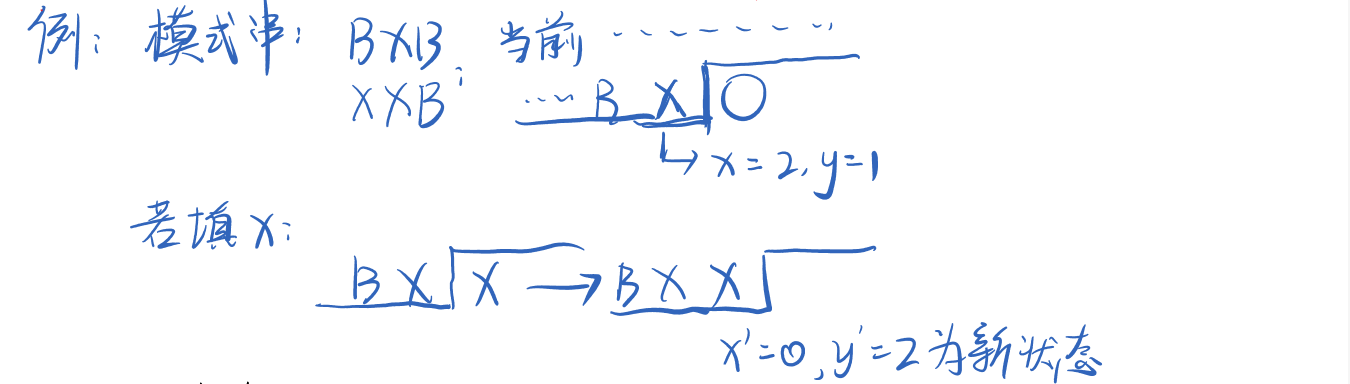
代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 15, M = 1030, mod = 1e9 + 7;
int n, m, c, p, f[2][M][N][N], S[2][N];
int fail[2][N], T[2][N][3];
string str[2];
void init(string str[]) {
	memset(f, 0, sizeof f), memset(S, 0, sizeof S);
	memset(fail, 0, sizeof fail), memset(T, 0, sizeof T);
	for (int i = 0; i < 2; i++) // 字符串转化成数组
		for (int j = 0; j < c; j++) 
			S[i][j + 1] = (str[i][j] == 'X' ? 2 : ((str[i][j] == 'B') ? 1 : 0));
	S[0][0] = S[1][0] = S[0][c + 1] = S[1][c + 1] = -1; // 处理边界, 方便后面KMP
	for (int k = 0; k < 2; k++) {
		for (int i = 2, j = 0; i <= c; fail[k][i++] = j) { // KMP
			while (j && S[k][i] != S[k][j + 1]) j = fail[k][j];
			if (S[k][i] == S[k][j + 1]) j++;
		} 
		for (int i = 0; i <= c; i++)                       // 处理To数组
			for (int ch = 0, j = i; ch <= 2; T[k][i][ch++] = j, j = i) {
				// cout << "i: " << i << " ch: " << ch << endl;
				while (j && S[k][j + 1] != ch) j = fail[k][j];
				if (S[k][j + 1] == ch) j++;
			}
	}
}
signed main() {
	cin >> n >> m >> c >> p;
	while (p-- && cin >> str[0] >> str[1]) {
		init(str);
		int cur = 0, S = 1 << (m - c + 1);
		f[0][0][0][0] = 1;
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				memset(f[cur ^ 1], 0, sizeof f[cur ^ 1]); // 滚动数组
				for (int k = 0; k < S; k++) // 枚举轮廓
					for (int x = 0; x <= c; x++)  // 枚举 x 
						for (int y = 0; y <= c; y++) // 枚举 y  
							if (f[cur][k][x][y]) // 常数优化, 值为 0 的时候以下操作无意义
								for (int ch = 0; ch <= 2; ch++) {
									int tk, tx = T[0][x][ch], ty = T[1][y][ch];
									// 计算 k'
									if (j < c) tk = k;
									else {
										tk = k | (1 << (j - c));
										if (tx ^ c) tk ^= 1 << (j - c);
									}
									if (ty == c && (k & (1 << (j - c)))) continue;
									if (j == m) f[cur ^ 1][tk][0][0] = (f[cur ^ 1][tk][0][0] + f[cur][k][x][y]) % mod;
									else f[cur ^ 1][tk][tx][ty] = (f[cur ^ 1][tk][tx][ty] + f[cur][k][x][y]) % mod;
								}
				cur ^= 1; // 滚动数组
			}
		}
		int ans = 0, t = 1;
		for (int k = 0; k < S; k++) ans = (ans + f[cur][k][0][0]) % mod;
		// 计算答案就是 n + 1 行, 枚举第 n 行所有轮廓相加
		for (int i = 1; i <= n * m; i++) t = 1ll * t * 3 % mod; // 注意爆 int
		cout << ((t - ans) % mod + mod) % mod << endl;
	}
	return 0;
}