积分上限的函数及其导数
设 \(f(x)\) 在区间 \([a,b]\) 上连续,\(x\)为 \([a,b]\) 上任意一点,则\(f(x)\)在 \([a,b]\) 区间也是连续的
因此定积分: \(\int_{a}^{x} f(t)dt\) 存在 (为便于区别,积分变量采用\(t\))
故对任意 \(x \in [a,b]\),有唯一确定的数 \(\int_{a}^{x} f(t)dt\) 与之对应
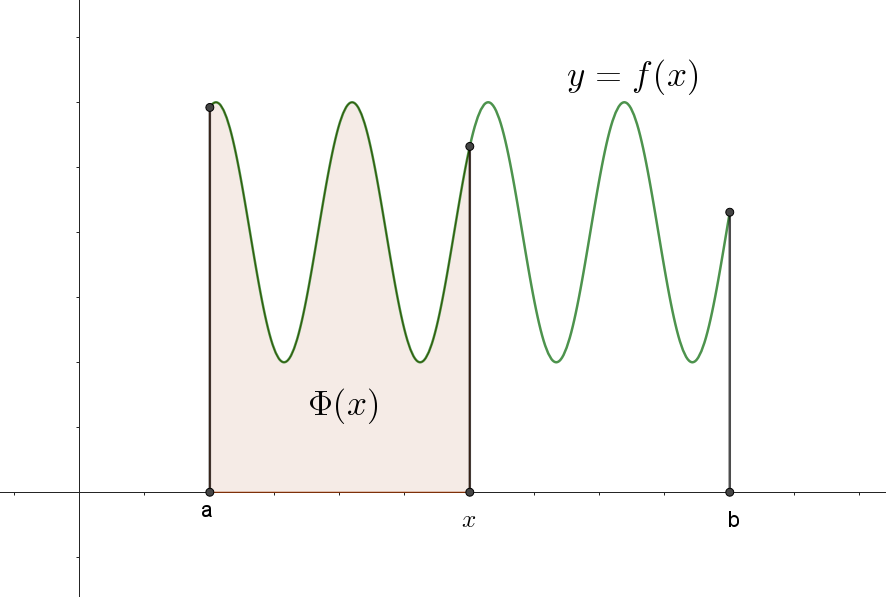
由此在 \([a,b]\) 上定义了一个新的函数,称其为积分上限的函数,记作 \(\Phi (x)\) (如下图) ,即:
\[\Phi (x)=\int_{a}^{x} f(t)dt , \enspace (a \le x \le b)
\]
Theorem1
expression
若函数 \(f(x)\) 在区间 \([a,b]\) 上连续,则积分上限的函数:
\[\Phi(x)=\int_{a}^{x} f(t)dt
\]
在 $[a,b] $ 上连续可导,并且它的导数为:
\[\Phi' (x)= \frac{d}{dx} \int_{a}^{x} f(t)dt=f(x),
\enspace \enspace
(a\le x \le b)
\]
proof step 1
设自变量 \(x\) 有增量 \(\Delta x\), 使得: $x+\Delta x \in [a,b] $, 则:
\[\begin{align}
\Delta \Phi=\Phi(x+\Delta x)-\Phi(x)
\\ \\
=\int_{x}^{x+\Delta x} f(t) dt-\int_{a}^{x} f(t) dt
\\ \\
\text { 设: }x+\Delta x=h, \quad (a\le x\le h )
\\ \\
\text { 根据定积分性质 2 可加性: }
\\ \\
\int_{a}^{h} f(t) dt=\int_{a}^{x} f(t) dt+\int_{x}^{h} f(t) dt
\\ \\
\Rightarrow \int_{a}^{x} f(t) dt+\int_{x}^{h} f(t) dt-\int_{a}^{x} f(t) dt=\int_{x}^{h} f(t) dt
\\ \\
\Delta \Phi=\int_{x}^{x+\Delta x} f(t) dt
\end{align}
\]
proof step 2
Invoke01: 性质6_积分中值定理
根据 Invoke01, 存在点 \(\xi\) 介于 \(x\) 与 \(x+\Delta x\)之间,使得:
\[\Delta \Phi =\int_{x}^{x+\Delta x}f(t)dt
=f(\xi)(x+\Delta x-x)
\\ \\
\Rightarrow f(\xi)\Delta x
\\ \\
\frac{\Delta \Phi}{\Delta x}= f(\xi),
\quad
(x\le \xi \le x+\Delta x)
\]
又因为$ f(x)$ 在 \([a,b]\) 上连续,且当\(\Delta x \to 0\)时,\(\xi\to x\),所以:
\[\begin{eqnarray}
\Phi '(x)=\lim_{\Delta x\to 0}\frac{\Delta\Phi}{\Delta x}
=\lim_{\Delta x\to 0} f(\xi)
\\ \\
已知: x\le \xi \le (x+\Delta x)
\\ \\
\Delta x \to0 = (\xi-x) \to 0
\\
得: \enspace \xi \to x
\\ \\
\lim_{\Delta x\to 0} f(\xi)=\lim_{\xi \to x} f(\xi)
\\ \\
\because \xi \to x
\\ \\
\therefore \lim_{\xi \to x} f(\xi) = f(x)
\end{eqnarray}
\]
此定理肯定了连续函数的原函数是存在的,即:
\[\Phi '(x)=\left[
\int_{a}^{x} f(t) dt
\right]^{\prime}=f(x)
\]
还表明了定积分与原函数之间的关系
Theorem2
Theorem: 牛顿-莱布尼茨公式
expression
如果 \(F(x)\) 是连续函数 \(f(x)\) 在区间 \([a,b]\) 上的一个原函数,则:
\[\int_{a}^{b} f(x)dx=F(b)-F(a)
\]
proof
已知 \(F(x)\) 是\(f(x)\)的一个原函数,根据Theorem1,积分上限函数 \(\Phi (x)\) 也是\(f(x)\)的一个原函数
根据来自不定积分的概念介绍,两个原函数之间的差别为常数\(C\),即:
\[
\begin{eqnarray}
\because F(x)-\Phi(x)=C, \enspace (a \leqslant x \leqslant b)
\\ \\
F(a)-\Phi(a)=C
\\ \\
F(b)-\Phi(b)=C
\\ \\
F(a)-\Phi(a)=F(b)-\Phi(b)
\\ \\
F(a)-F(b)=\Phi(a)-\Phi(b)
\\ \\
\because \int_{a}^{a} f(t) dt 的上下界相等
\\ \\
\therefore F(a)=\Phi(a)=\int_{a}^{a} f(t) dt=0
\\ \\
F(b)=\Phi(b)=\int_{a}^{b} f(t) dt
\\ \\
F(a)-F(b)=\Phi(a)-\Phi(b)
\\ \\
=\int_{a}^{a} f(t) dt-\int_{a}^{b} f(t) dt
\\ \\
=0-\int_{a}^{b} f(t) dt
\\ \\
-\int_{a}^{b} f(t) dt =-F(b)
\\ \\
\because F(a)=0, \enspace \enspace F(b)=\int_{a}^{b} f(t) dt
\\ \\
\therefore F(b)-F(a)=\int_{a}^{b} f(t) dt
\end{eqnarray}
\]
牛顿-莱布尼茨公式,也被称为微积分基本公式,在微积分之中非常重要
牛顿-莱布尼茨公式也可记作:
\[\begin{array}{c}
\int_{a}^{b} f(x)dx=\left[
F(x)
\right]^{b}_{a}
\\ \\
或
\\ \\
\int_{a}^{b} f(x)dx=
F(x)|^{b}_{a}
\end{array}
\]




