定积分几何意义
如下图所示，有一个由三条直线与一条曲线围成的特殊四边形，现在想求这个特殊四边形的面积(设为\(S\))
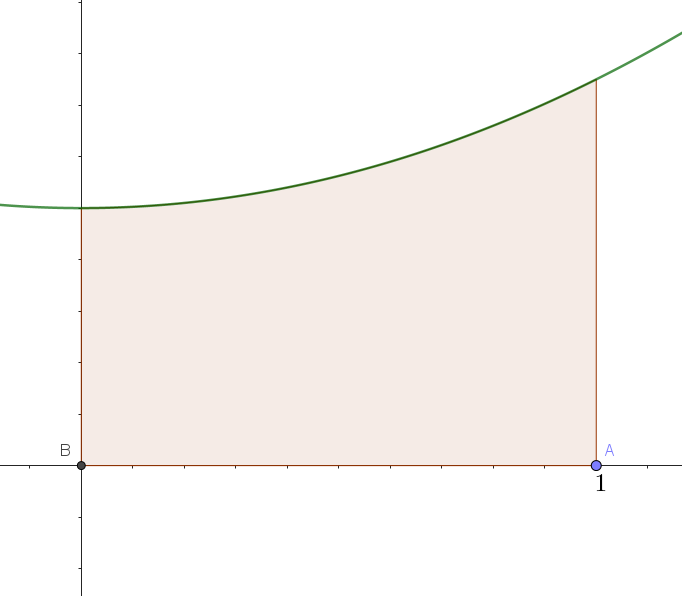
如下图所示，用\(n\)个矩形去拟合特殊四边形，然后算出这些矩形的面积之和。
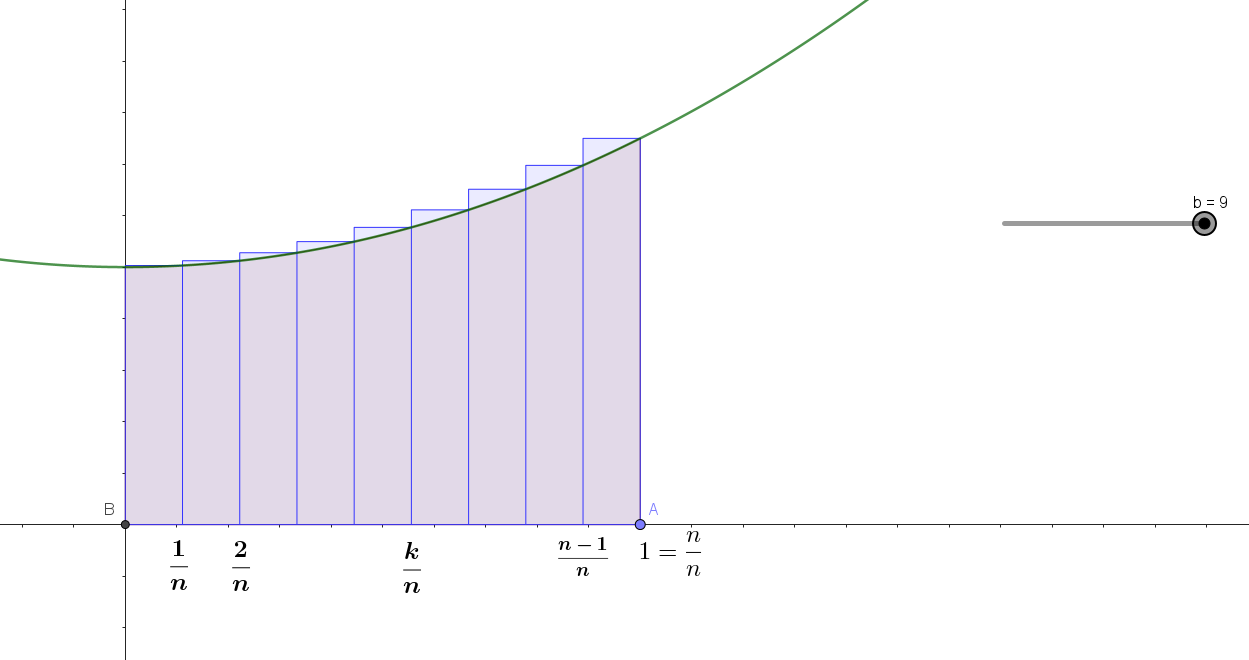
若\(n \to +\infin\)，那么\(n\)个矩形的面积之和就无限趋近于\(S\)
用数学语言表达即为:
已知图中曲线的方程为\(f(x)\)
\(n\)代表全部矩形的总数（ \(0 < n \le 1\) ）
\(k\)代表任意一个矩形的序号（ \(0 \le k \le 1\) ）
\[\begin{align}
S \approx f(\frac{1}{n})\frac{1}{n} + f(\frac{2}{n})\frac{1}{n} + ... + f(\frac{k}{n})\frac{1}{n} + ... +
f(\frac{n}{n})\frac{1}{n}
\\ \\
f(\frac{1}{n})\frac{1}{n} + f(\frac{2}{n})\frac{1}{n} + ... + f(\frac{k}{n})\frac{1}{n} + ... +
f(\frac{n}{n})\frac{1}{n}
= \sum_{k=1}^{n}f(\frac{k}{n}) \frac{1}{n}
\\ \\
S \approx \lim_{n\to +\infty} \sum_{k=1}^{n}f(\frac{k}{n}) \frac{1}{n}
\\ \\
\lim_{n\to +\infty} \sum_{k=1}^{n}f(\frac{k}{n}) \frac{1}{n}
= \int_{0}^{1} f(x)dx
\\ \\
\frac{k}{n}对应 x, \quad f(\frac{k}{n})对应 f(x), \quad \frac{1}{n} 对应 dx
\end{align}
\]
