三角函数之诱导公式
First
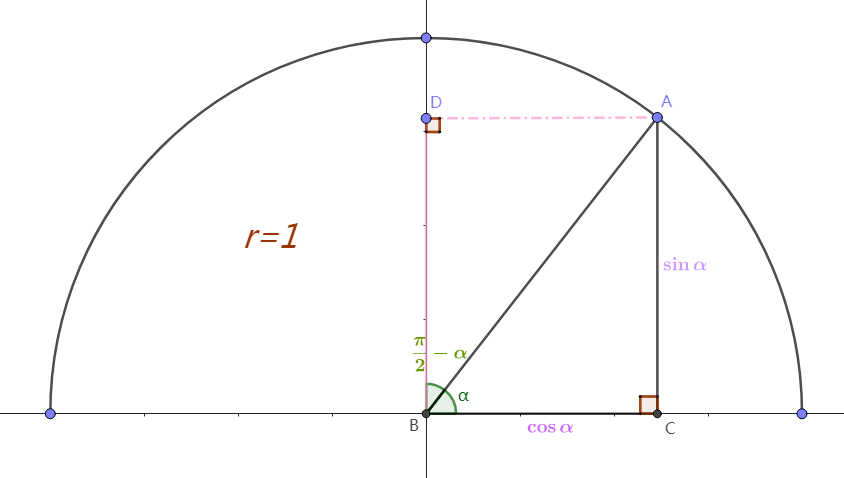
如上图:
\[\begin{eqnarray}
已知: \enspace AC=\sin\alpha,BC=\cos\alpha
\\ \\ \\
\sin\left(\frac{\pi}{2}-\alpha\right)=\frac{AD}{AB}=\frac{BC}{AB}=\cos\alpha
\\ \\
诱导公式组0.1: \enspace \sin\left(\frac{\pi}{2}-\alpha\right)=\cos\alpha
\\ \\ \\
\cos\left(\frac{\pi}{2}-\alpha\right)=\frac{BD}{AB}=\frac{AC}{AB}=\sin\alpha
\\ \\
诱导公式组0.2: \enspace \cos\left(\frac{\pi}{2}-\alpha\right)=\sin\alpha
\\ \\ \\
\tan\left(\frac{\pi}{2}-\alpha\right)=\frac{AD}{BD}=\frac{BC}{AC}=\frac{\cos\alpha}{\sin\alpha}
\\ \\
\because \tan\alpha=\frac{\sin\alpha}{\cos\alpha}
\\ \\
诱导公式组0.3: \enspace \tan\left(\frac{\pi}{2}-\alpha\right)=\frac{1}{\tan\alpha}=\cot\alpha
\\ \\ \\
诱导公式0.1: \enspace \sin\left(\frac{\pi}{2}-\alpha\right)=\cos\alpha
\\
诱导公式0.2: \enspace \cos\left(\frac{\pi}{2}-\alpha\right)=\sin\alpha
\\
诱导公式0.3: \enspace \tan\left(\frac{\pi}{2}-\alpha\right)=\frac{1}{\tan\alpha}=\cot\alpha
\end{eqnarray}
\]
Second: 奇偶性质
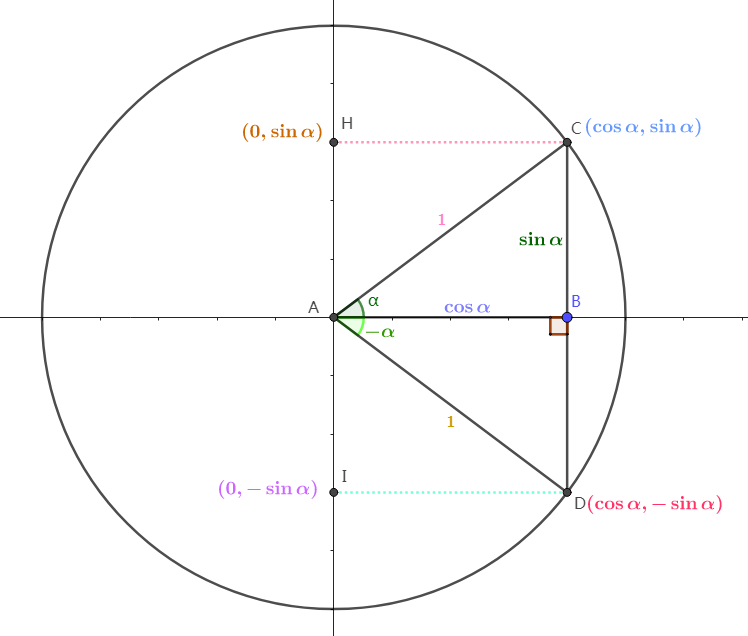
如上图:
\[\begin{align}
\triangle ABC=\triangle ABD
\\
\angle BAC=\alpha,\angle DAB=-\alpha
\\
\angle BAC=\angle DAB
\\ \\
在 \triangle ABD
\\
\sin(-\alpha)=\frac{BD}{AD}=-\sin\alpha
\\
\therefore\sin(-\alpha)=-\sin\alpha
\\ \\
\cos(-\alpha)=\frac{AB}{AD}=\cos\alpha
\\
\therefore\cos(-\alpha)=\cos\alpha
\\ \\
诱导公式1.0(奇函数):\enspace \sin(-\alpha)=-\sin\alpha
\\
诱导公式1.1(偶函数):\enspace \cos(-\alpha)=\cos\alpha
\end{align}
\]
Third
\[\begin{align}
标三零:\\
\sin(\frac{\pi}{2}+\alpha)\Rightarrow\sin[\frac{\pi}{2}-(-a)]
\\
根据公式0.1:
\\
\sin\left[\frac{\pi}{2}-\left(-a\right)\right]=\cos\left(-a\right)
\\ \\
根据公式1.1:
\\
\sin[\frac{\pi}{2}-(-a)]=\cos\alpha
\\
\therefore\sin\left(\frac{\pi}{2}+\alpha\right)=\cos\alpha
\\ \\ \\
标三一:\\
\cos(\frac{\pi}{2}+\alpha)\Rightarrow\cos[\frac{\pi}{2}-(-\alpha)]
\\
根据公式0.2:
\\
\cos[\frac{\pi}{2}-(-\alpha)]=\sin(-\alpha)
\\ \\
根据公式1.0:
\\
\cos[\frac{\pi}{2}-(-\alpha)]=-\sin\alpha
\\
\therefore\cos(\frac{\pi}{2}+\alpha)=-\sin\alpha
\\ \\ \\
诱导公式2.0:\enspace \sin\left(\frac{\pi}{2}+\alpha\right)=\cos\alpha
\\
诱导公式2.1:\enspace \cos\left(\frac{\pi}{2}+\alpha\right)=-\sin\alpha
\end{align}
\]
Fourth
\[\begin{align}
求证: \quad 1+\tan^{2}x=\sec^{2}x
\\ \\
\Rightarrow 1+\frac{\sin^{2}x}{\cos^{2}x}=\frac{\cos^{2}x}{\cos^{2}x}+\frac{\sin^{2}x}{\cos^{2}x}
=\frac{\cos^{2}x+\sin^{2}x}{\cos^{2}x}
\\ \\
\because \cos^{2}x+\sin^{2}x=1
\\ \\
\therefore \frac{\cos^{2}x+\sin^{2}x}{\cos^{2}x}=\frac{1}{\cos^{2}x}=(\frac{1}{\cos x})^{2}
\\ \\
\because \frac{1}{\cos x}=\sec x
\\ \\
\therefore(\frac{1}{\cos x})^{2}=\sec^{2}x
\\ \\
\therefore 1+\tan^{2} x=\sec^{2}x
\end{align}
\]
