三角函数之和差化积公式
- 知识点1:三角函数奇偶性: \(\sin(-\theta)=-\sin\theta, \quad \cos(-\theta)=\cos\theta\)
\[\begin{align}
(诱导公式1.0)\enspace \cos(\frac{\pi}{2}+\alpha)=-\sin\alpha
\\
(诱导公式1.1)\enspace \cos(\pi+\alpha)=-\cos\alpha
\\
(诱导公式1.2)\enspace \cos(\frac{\pi}{2}-\alpha)=\sin\alpha
\end{align}
\]
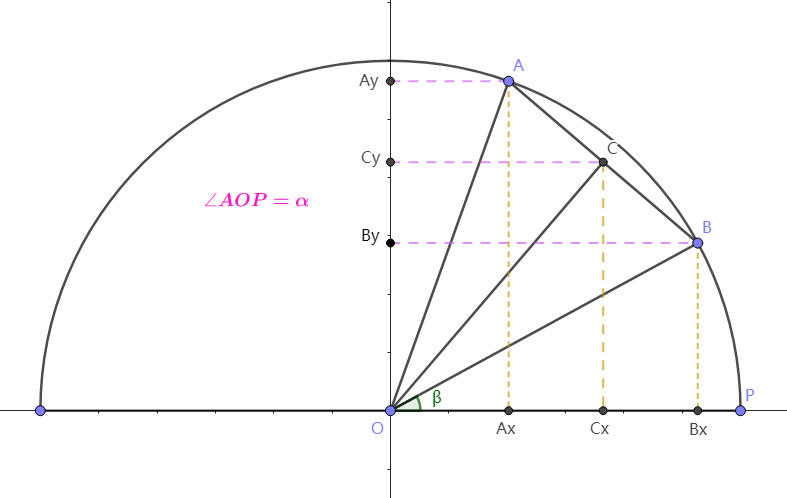
如上图:
单位半圆的半径为1,\(\triangle AOB\)为等腰三角形。
点\(C\)为线段\(AB\)之中点,连接\(CO\)。
根据等腰三角形的性质,\(CO\) 是 \(△AOB\) 的角平分线和垂直平分线。
\(CO\) 垂直于 \(AB\),\(CO\) 将 \(△AOB\) 的顶角 \(∠AOB\) 平分。
角度参数
\[\begin{align}
设\angle AOP=\alpha
\\
设\angle BOP=\beta
\\
则\angle AOB=\alpha-\beta
\\ \\
\angle BOC=\angle A O C =\frac{\alpha-\beta}{2}
\\
\angle POC=\beta+\frac{\alpha-\beta}{2}=\frac{\alpha+\beta}{2}
\end{align}
\]
极坐标壹
\[\begin{align}
标一:
\\
在 \triangle AOA_{x},\quad OA_{x}=\cos \alpha
\\
AA_{x}=OAy=\sin \alpha
\\ \\
标二:
\\
在 \triangle BOB_{x}, \quad OB_{x}=\cos \beta,
\\
BB_{x}=OB_{y}=\sin \beta
\\ \\
C_{x}O-OA_{x}=OB_{x}-C_{x}O
\\
2C_{x}O=OA_{x}+OB_{x}=\cos \alpha+\cos \beta
\\
C_{x}O=\frac{\cos \alpha+\cos \beta}{2}
\\ \\
标三: \\
O A_{y}-C_{y} O=C_{y} O-O B_{y}
\\ \\
2 C_{y} O=O A_{y}+O B_{y}=\sin \alpha+\sin \beta
\\ \\
C_{y} O=\frac{\sin \alpha+\sin \beta}{2}
\\ \\
转化为极坐标:\\
C_{1}\left(C_{x} O, C_{y} O\right) \Rightarrow
\left(\frac{\cos \alpha+\cos \beta}{2},
\enspace
\frac{\sin \alpha+\sin \beta}{2}\right)
\end{align}
\]
极坐标贰
\[\begin{align}
在 \triangle AOC
\\
\cos\frac{\alpha-\beta}{2}=\frac{CO}{OA}
\\
CO=\cos\frac{\alpha-\beta}{2}
\\ \\ \\
在\triangle COC_{x}
\\ \\
\cos\frac{\alpha+\beta}{2}=\frac{C_{x}O}{CO}=\frac{C_{x}O}{\cos\frac{\alpha-\beta}{2}}
\\ \\
C_{x}O=\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}
\\ \\ \\
在\triangle COCx
\\
\sin\frac{\alpha+\beta}{2}=\frac{CC_{x}}{CO}
=\frac{CC_{x}}{\cos \frac{\alpha-\beta}{2}}
\\ \\
CyO=CC_{x}=\cos\frac{\alpha-\beta}{2}\sin\frac{\alpha+\beta}{2}
\\ \\
转化为极坐标:
\\
C_{2}(C_{x}O,CC_{x})\Rightarrow(\cos\frac{\alpha-\beta}{2}\cos\frac{\alpha+\beta}{2},
\enspace
\cos\frac{\alpha-\beta}{2}\sin\frac{\alpha+\beta}{2})
\end{align}
\]
公式结论组
\[\begin{align}
两个极坐标相等: \enspace C_{1}=C_{2}
\\ \\
\frac{\cos\alpha+\cos\beta}{2}=\cos\frac{\alpha-\beta}{2}\cos\frac{\alpha+\beta}{2}
\\
结论组1.0: \enspace \cos\alpha+\cos\beta=2\cos\frac{\alpha-\beta}{2}\cos\frac{\alpha+\beta}{2}
\\ \\
\frac{\sin\alpha+\sin\beta}{2}=\cos\frac{\alpha-\beta}{2}\sin\frac{\alpha+\beta}{2}
\\
结论组1.1: \enspace \sin\alpha+\sin\beta=2\cos\frac{\alpha-\beta}{2}\sin\frac{\alpha+\beta}{2}
\\ \\ \\
引用结论组1.1: \\
\sin\alpha+\sin\left(-\beta\right)=
2\frac{\cos\alpha-\left(-\beta\right)}{2}
\sin\frac{\alpha+\left(-\beta\right)}{2}
\\ \\
结论组2.0: \enspace \sin\alpha-\sin\beta=2\cos\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}
\\ \\ \\
调用结论组1.0: \\
\cos\alpha+(\pi+\beta)=2\cos\frac{\alpha+(\pi+\beta)}{2}
\cos\frac{\alpha-(\pi+\beta)}{2}
\\ \\ \\
分式1,援引诱导公式:\\
\cos\frac{\alpha+(\pi+\beta)}{2}\rightarrow\cos(\frac{\pi}{2}+\frac{\alpha+\beta}{2})=
-\sin\frac{\alpha+\beta}{2}
\\ \\ \\
分式2:
\\
\cos\frac{\alpha-\left(\pi+\beta\right)}{2}
=
\cos\frac{-\pi+\alpha-\beta}{2}
\\ \\
\Rightarrow\cos[-\frac{\pi}{2}+(\frac{\alpha-\beta}{2})]
\\
\Rightarrow\cos[-(\frac{\pi}{2}-(\frac{\alpha-\beta}{2}))]
\\ \\
利用奇偶性: \\
\Rightarrow\cos[\frac{\pi}{2}-(\frac{\alpha-\beta}{2})]
\\ \\
调用诱导公式:
\\
\Rightarrow\sin\frac{\alpha-\beta}{2}
\\ \\ \\
结论组2.1: \enspace
\cos\alpha-\cos\beta=-2\sin\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}
\end{align}
\]
Summarize
\[\begin{align}
结论组1.0: \enspace \cos\alpha+\cos\beta=2\cos\frac{\alpha-\beta}{2}\cos\frac{\alpha+\beta}{2}
\\ \\
结论组1.1: \enspace \sin\alpha+\sin\beta=2\cos\frac{\alpha-\beta}{2}\sin\frac{\alpha+\beta}{2}
\\ \\
结论组2.0: \enspace \sin\alpha-\sin\beta=2\cos\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}
\\ \\
结论组2.1: \enspace
\cos\alpha-\cos\beta=-2\sin\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2}
\end{align}
\]



 浙公网安备 33010602011771号
浙公网安备 33010602011771号