三角函数之二倍角公式
preamble
-
前置1：圆周角定理：圆周角等于圆心角的一半，因此直径所对的圆周角等于直角
-
前置2：三角形外角定理: 三角形的一个外角等于它不相邻的两个内角之和
-
公式1：\(\sin^{2} \theta+\cos^{2} \theta=1\)
description
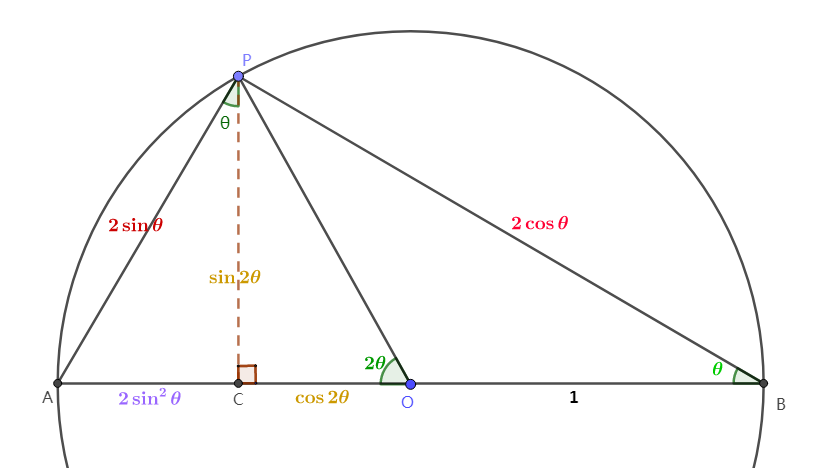
如上图，
\(\Delta BPA\) 内接半圆，设半圆的半径为1，圆点为\(O\)，设 \(\angle PBA\) 为 \(\theta\)。
作垂线 \(PC\) 垂直于直径。
根据前置1，\(\angle BPA\) 为直角；
根据前置2，\(\angle POA = 2 \theta\)；
已知 \(\Delta PAC\) 与 \(\Delta PAB\) 为直角三角形，且： \(\angle PAC=\angle PAB\)，
所以 \(\Delta PAC\) 与 \(\Delta PAB\) 相似，
所以 \(\angle APC = \theta\)
procedure
\[\begin{align}
在 \triangle PCO
\\
CO=\cos 2 \theta, \quad PC=\sin 2 \theta
\\ \\ \\
在 \triangle BPA
\\
\sin \theta=\frac{AP}{AB}=\frac{A D}{2}, AP=2 \sin \theta
\\
\cos \theta=\frac{PB}{AB}=\frac{P B}{2}, PB=2 \cos \theta
\\ \\ \\
在 \triangle PAC
\\
\sin \theta=\frac{AC}{AP}=\frac{A C}{2 \sin \theta}
\\
AC=2 \sin \theta \cdot \sin \theta=2 \sin ^{2} \theta
\\ \\ \\
在 \triangle PBC
\\
\sin \theta=\frac{PC}{PB}=\frac{\sin 2 \theta}{2 \cos \theta}
\\ \\
定论1: \quad \sin 2 \theta=2 \cos \theta \sin \theta
\\ \\ \\
CO=AO-AC
\\
定论2.1：\cos 2 \theta =1-2 \sin ^{2} \theta
\\ \\
引用公式1
\\
1-2 \sin ^{2} \theta =\left(\cos ^{2} \theta+\sin ^{2} \theta\right)-2 \sin ^{2} \theta
\\
定论2.2：\cos 2 \theta =\cos ^{2} \theta-\sin ^{2} \theta
\\ \\
引用公式1
\\
\cos ^{2} \theta-\sin ^{2} \theta =\cos ^{2} \theta-\left(1-\cos ^{2} \theta\right)
\\
定论2.3：\cos 2 \theta =2 \cos^{2} \theta-1
\end{align}
\]
conclusion
\[\begin{align}
定论1: \quad \sin 2 \theta=2 \cos \theta \sin \theta
\\ \\
定论2.1：\cos 2 \theta =1-2 \sin ^{2} \theta
\\ \\
定论2.2：\cos 2 \theta =\cos ^{2} \theta-\sin ^{2} \theta
\\ \\
定论2.3：\cos 2 \theta =2 \cos^{2} \theta-1
\end{align}
\]
