三角函数之半角公式
prologue
-
公式1: \(\quad \cos^{2}\theta+\sin^{2}\theta=1\)
-
前知识1: 三角形外角定理: 三角形的任意一个外角等于和它不相邻的两个内角之和
-
前知识2: 圆周角定理(该定理之证明会援引前知识1)，其中之一: 圆的直径所对的圆周角是直角
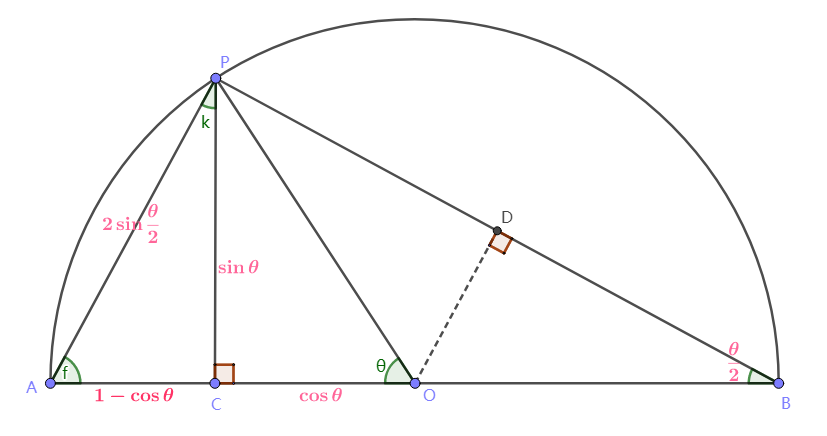
如上图，\(O\)为原点，\(PC\)垂直于直径\(AB\)，\(ＯＤ\)垂直于\(ＰＢ\)
设圆的半径为1，\(\angle POC=\theta\)。
\(\Delta POB\)为等腰三角形，\(\angle POC\)为\(\angle PBO\)的外角。
根据前知识1，\(\angle PBO=\frac{\theta}{2}\)
根据前知识2，\(\Delta BPA\)为直角三角形，\(\angle APB=90^{\circ}\)
First
\[\begin{align}
\cos^{2}\theta+\sin^{2}\theta=1, \quad (公式1)
\\ \\
\angle k+\angle f=90^{\circ}
\\
\frac{\theta}{2}+\angle f=90^{\circ}
\\
\therefore\angle k=\frac{\theta}{2}
\\ \\
OC=\cos\theta
\\
AC=1-\cos\theta
\\
PC=\sin\theta
\end{align}
\]
Second
\[\begin{align}
在\Delta PBC之中, \quad \tan\frac{\theta}{2}=\frac{\sin\theta}{1+\cos\theta}
\\ \\
在\Delta PAC之中, \quad \tan\frac{\theta}{2}=\frac{1-\cos\theta}{\sin\theta}
\\ \\
结果1:\enspace \tan\frac{\theta}{2}=\frac{\sin\theta}{1+\cos\theta}=\frac{1-\cos\theta}{\sin\theta}
\end{align}
\]
Third
\[\begin{align}
在\Delta PBA之中, \quad
\because \sin\frac{\theta}{2}=\frac{PA}{AB}
\\
\therefore PA=2\sin\frac{\theta}{2}
\\ \\
在\Delta PAC之中,(2\sin\frac{\theta}{2})^{2}=(1-\cos\theta)^{2}+
\sin^{2}\theta
\\ \\
2.1标:\enspace 4\sin^{2}\frac{\theta}{2}=1-2\cos\theta+\cos^{2}\theta+\sin^{2}\theta
\\
根据公式1
\\
2.2标:\enspace 4\sin^{2}\frac{\theta}{2}=2-2\cos\theta
\\ \\
\sin^{2} \frac{\theta}{2}=\frac{2(1-\cos \theta)}{4}
\\ \\
\sin ^{2} \frac{\theta}{2}=\frac{1-\cos \theta}{2}
\\ \\
结果2:\enspace \sin \frac{\theta}{2}= \pm \sqrt{\frac{1-\cos \theta}{2}}
\end{align}
\]
Fourth
\[\begin{align}
DB=DP=\cos \frac{\theta}{2}
\\ \\
PB=2\cos \frac{\theta}{2}
\\ \\
在\Delta PBC之中, \quad (2\cos \frac{\theta}{2})^{2}=(1+\cos\theta)^{2}+\sin^{2} \theta
\\ \\
4\cos^{2}\frac{\theta}{2}=1+2\cos\theta+\cos^{2}\theta+\sin^{2}\theta
\\
根据公式1
\\
4\cos^{2}\frac{\theta}{2}=1+2\cos\theta+1
\\ \\
\cos^{2}\frac{\theta}{2}=\frac{2+2\cos\theta}{4}
\\ \\
\cos^{2}\frac{\theta}{2}=\frac{1+\cos\theta}{2}
\\ \\
结果3:\enspace \cos\frac{\theta}{2}=\pm \sqrt[]{\frac{1+\cos\theta}{2}}
\end{align}
\]
