三角函数之互补角公式
互补角
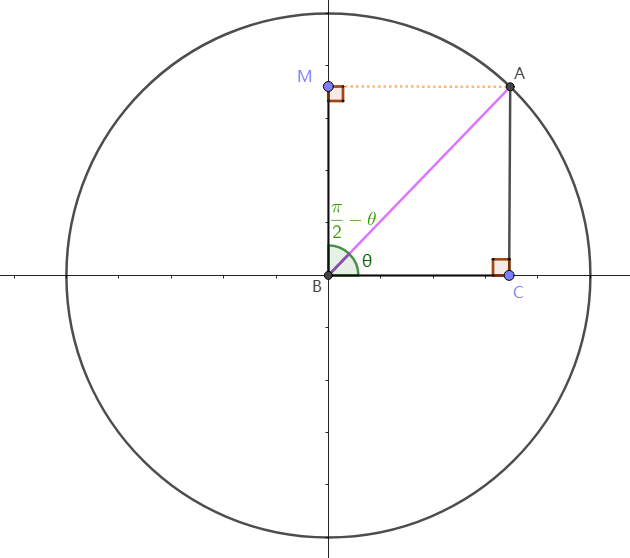
如上图：
\[\begin{eqnarray}
设AB=1, \quad
\angle ACB=\angle AMB=90^{\circ}
\\
则AC=BM, \quad
AM=BC
\\ \\
\because \angle ACB=\angle AMB=\frac{\pi}{2}
\\
\therefore \angle ABC=\theta, \quad
\angle ABM=\frac{\pi}{2}-\theta
\\ \\ \\
\sin\theta=\frac{AC}{AB}
\\ \\
\cos\theta=\frac{BC}{AB}
\\ \\
\tan \theta=\frac{AC}{BC}
\\ \\ \\
\sin (\frac{\pi}{2}-\theta)=\frac{AM}{AB}=\frac{BC}{AB}=\cos\theta
\\ \\
\cos\left(\frac{\pi}{2}-\theta\right)=\frac{BM}{AB}=\frac{AC}{AB}=\sin\theta
\\ \\
\tan\left(\frac{\pi}{2}-\theta\right)=\frac{AM}{BM}=\frac{BC}{AC}=\cot\theta
\end{eqnarray}
\]
