拉格朗日(Lagrange)中值定理
preamble
-
罗尔中值定理是理解拉格朗日中值定理的基础
-
罗尔中值定理是拉格朗日中值定理的1个特殊情况
-
泰勒中值定理是拉格朗日中值定理的推广
- Cite:
definition
若函数\(f(x)\)满足下列条件：
- \(f(x)\) 在闭区间\([a,b]\)上连续
- \(f(x)\) 在闭区间\((a,b)\)上可导
则在\((a,b)\)内至少存在一点 \(\xi\) , 使得\(f'(\xi)=\frac{f(b)-f(a)}{b-a}\)
等价形式： \(f(b)-f(a)=f'(\xi)(b-a)\), \(a< \xi <b\)
几何意义：
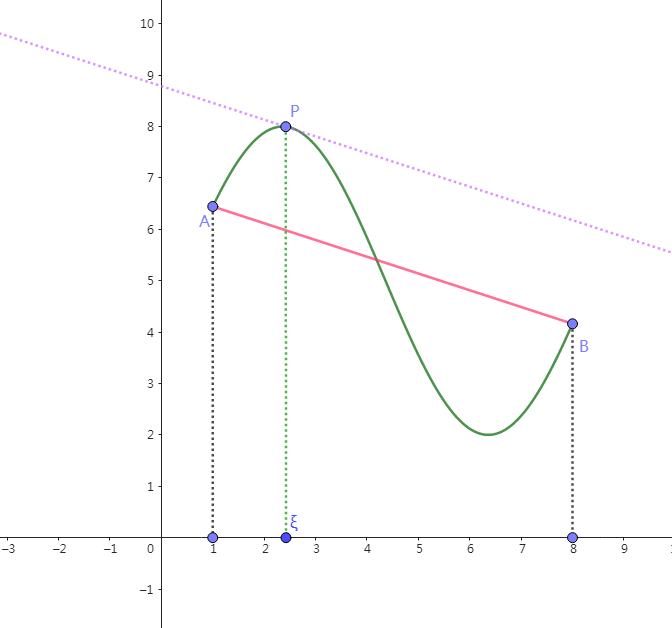
在满足定理条件的曲线\(y=f(x)\)上至少存在一点\(P(\enspace \xi,\enspace f(\xi)\enspace)\)，经过该点处的切线平行于曲线两端端点的连线\(AB\)
如下图所示：
attest
证明思路：构造一个原函数，以及利用罗尔中值定理
\[
\begin{align}
证明：f'(\xi)-\frac{f(b)-f(a)}{b-a}=0
\\ \\
构造原函数: W(x)=f(x)-\frac{f(b)-f(a)}{b-a} x
\\ \\
而W(x)的导数正是：W'(x)=f'(\xi)-\frac{f(b)-f(a)}{b-a}
\\ \\
将a、b两点代入W(x)： \
W(a)=f(a)-\frac{f(b)-f(a)}{b-a} a
\\ \\
\frac{f(a)b-f(a)a}{b-a} - \frac{f(b)a-f(a)a}{b-a}
=
\frac{f(a)b-f(a)a-f(b)a+f(a)a}{b-a}
\\ \\
得：W(a)=\frac{f(a)b-f(b)a}{b-a}
\\ \\
W(b)=f(b)-\frac{f(b)-f(a)}{b-a} b
\\ \\
\frac{f(b)b-f(b)a}{b-a}-\frac{f(b)b-f(a)b}{b-a}
=
\frac{f(b)b-f(b)a-f(b)b+f(a)b}{b-a}
\\ \\
得：W(b)=\frac{f(a)b-f(b)a}{b-a}
\\ \\
\therefore W(a)=W(b)
\\
且W(x)满足罗尔中值定理中的对于在开闭区间内连续与可导的两条条件
\\
故存在 \xi \in (a,b)
\\
便可以据罗尔中值定理推出: W'(\xi)=0
\\ \\
\because W'(\xi)=f'(\xi)-\frac{f(b)-f(a)}{b-a}=0
\\ \\
\therefore f'(\xi)=\frac{f(b)-f(a)}{b-a}
\\ \\
证明成立
\end{align}
\]
