导数之如何理解$f(x)$在某一区间内可导
设函数\(y=|x|\),其函数图像如下所示:
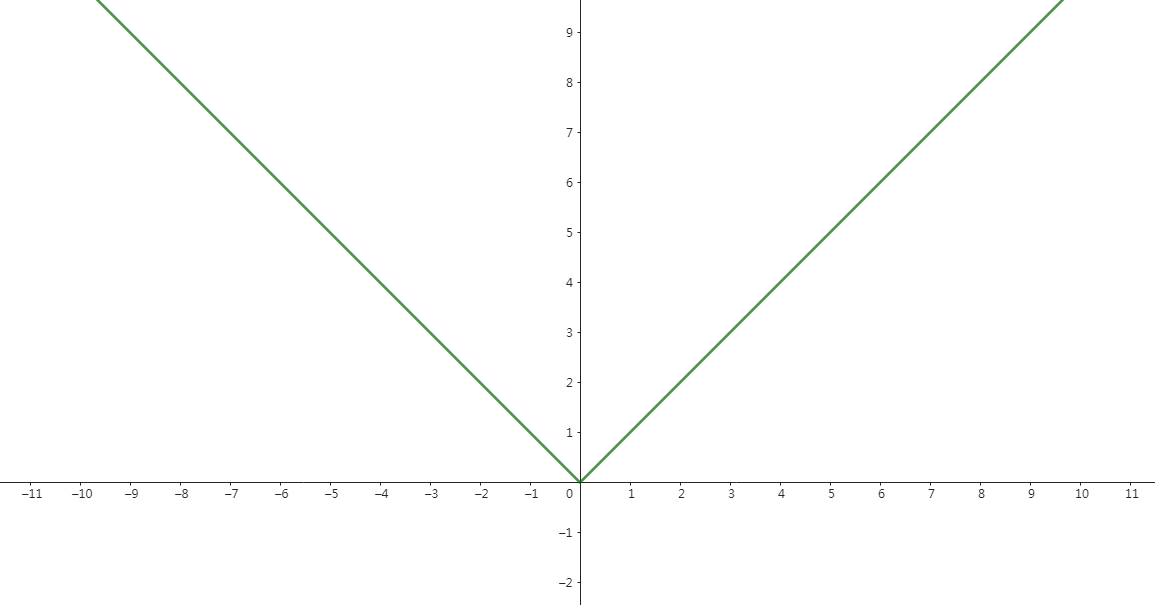
可见\(x=0\)时,\(y=0\)。 其函数图像于\(x=0\)处存在1个“棱角”。
这意味着\(y\)在\(x=0\)处是不可导的,因为\(y\)呈现的函数图像是有棱角的,“非光滑的”,即不是曲线。
反之,若已知另一个函数\(f(x)\)在例如开区间\((a,b)\)内是可导的,则\(f(x)\)在开区间\((a,b)\)所呈现的函数图像是“光滑的”,等同于曲线。
设函数\(y=|x|\),其函数图像如下所示:

可见\(x=0\)时,\(y=0\)。 其函数图像于\(x=0\)处存在1个“棱角”。
这意味着\(y\)在\(x=0\)处是不可导的,因为\(y\)呈现的函数图像是有棱角的,“非光滑的”,即不是曲线。
反之,若已知另一个函数\(f(x)\)在例如开区间\((a,b)\)内是可导的,则\(f(x)\)在开区间\((a,b)\)所呈现的函数图像是“光滑的”,等同于曲线。
