通过物理分析解释隐函数求导

隐函数曲线(implicit curve):
形如 \(x^{2}+y^{2}=5^{2}\) ,满足某种关于变量\(x\)和\(y\)的性质,或在此种性质下所有\((x,y)\)点的集合

---

---

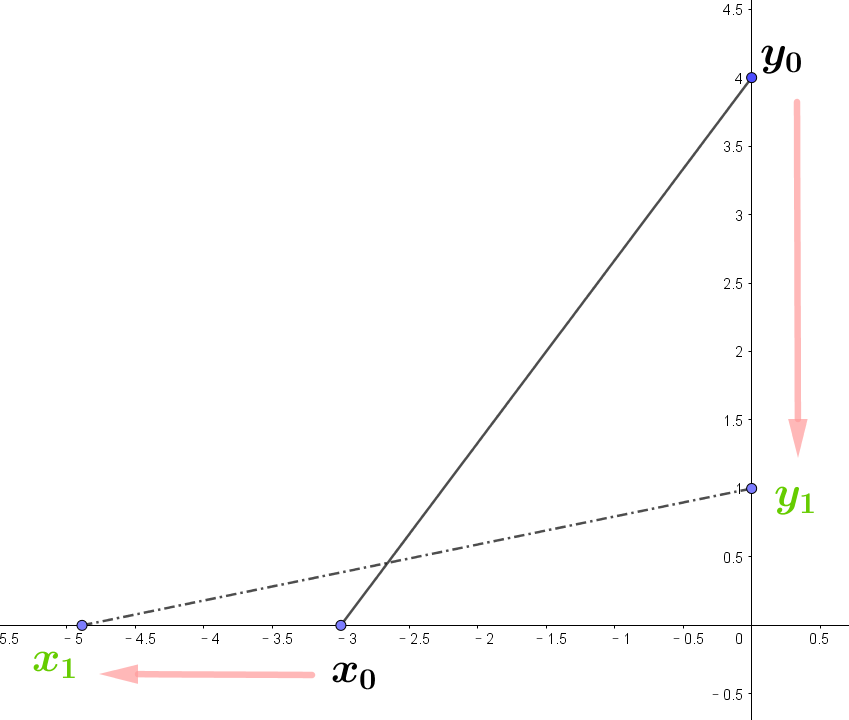
如上图所示:
假设地面为横坐标轴,垂直于地面的墙面为纵坐标轴,图中斜线长度固定为5,此处将斜线视为一架斜靠在墙上的梯子.
现在梯子顶端会沿着墙面,向地面滑下去\((y_{0} \to y_{1})\).
梯子底端也随之向左侧移动\((x_{0} \to x_{1})\).
梯子顶端以\(1m/s\)的速度沿墙下滑,
问,在梯顶开始下滑的那一瞬间,梯底向左运动的瞬时速度为多少?

设时间变量为t,
梯顶离地之距离用函数\(y=y(t)\)来表示.
梯底离地之距离用函数\(x=x(t)\)来表示.
则可得方程: \(x^{2}(t)+t^{2}(t)=5^{2},\)
这个方程可以视作一个隐函数.

如果对方程求导\(( \frac{d[x^{2}(t)+y^{2}(t)]}{ dt} ),\)
其实是在问: 时间\(t\)变化了一个量\((dt)\)之后,\(y\)会减少一个量\((dy)\),\(x\)会增加一个量\((dx)\),
那么 此一过程中产生变化的总量之值的平均变化率 是多少?
(ps: \(\frac{dx}{dt}\)表示 \(x\) 根据时间变化的变化率)

\[\frac{d[x^{2}(t)+y^{2}(t)]}{ dt}= 2x(t)\frac{dx}{dt} + 2y(t)\frac{dy}{dt} = 0 \]

\[\\ \\ \]

$
[x^{2}(t)]'=2x(t)\frac{dx}{dt} $ : \(2x(t)dx\)表示因为\(x\)变化而导致的\(x^{2}\)的变化量,然后再除以\(dt\).

同理,$[y^{2}(t)]'=2y(t)\frac{dy}{dt} $

回到题目所求,因为梯顶下滑速度为\(1m/s\),

\[\therefore \frac{dy}{dt}=-1 (y不断缩小) \]

\[\\ \\ \]

\[\because y=4,\quad x=3 \]

\[\\ \\ \]

\[\Rightarrow 2(3)\frac{dx}{dt}+2(4)(-1)=0 \]

\[\\ \\ \]

\[\Rightarrow \frac{dx}{dt}=\frac{4}{3} (m/s) \]