第一重要极限
第二重要极限证明:https://www.cnblogs.com/Preparing/p/16576649.html
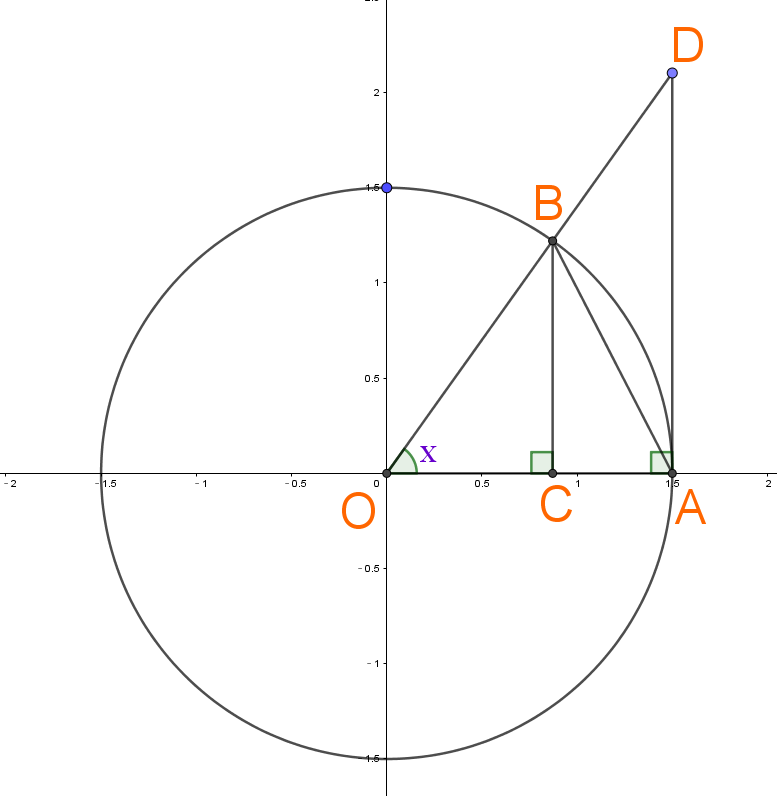
\[\begin{align}
证明极限\lim_{x\to 0}\frac{\sin{x}}{x}=1
\\ \\
设∠AOB=x(0<x<\frac{π}{2}) \\
\because △AOB面积 < 扇形AOB面积 < △AOD面积
\\
\Rightarrow \frac{\sin{x}\cdot r\cdot r}{2} < \frac{xπr^{2}}{2π} <\frac{\tan{x}\cdot r\cdot r}{2}
\\ \\
约去\frac{1}{2}和r^{2}: \sin{x} < x < \tan{x} \\
除以\sin{x}: 1<\frac{x}{\sin{x}}<\frac{\tan{x}}{\sin{x}}\\
=1<\frac{x}{\sin{x}}<\frac{1}{\cos{x}}
\\ \\
将不等式中每个数都变为倒数,原大小关系会变向: \\
1>\frac{\sin{x}}{x}>\cos{x} \\
\\ \\
\because \cos{x}为偶函数[\cos{x}=\cos (-x)]\\
而\frac{\sin{x}}{x}=\frac{\sin (-x)}{-x} \\
\therefore 不等式在x \in [-\frac{π}{2}, 0) 照样成立
\\ \\
\therefore \cos{x}<\frac{\sin{x}}{x}<1的定义域:x\in[-\frac{π}{2}, \frac{π}{2}],x\ne0
\\ \\
\because \lim_{x\to 0}\cos{x}=1
\\ \\
再由迫敛定理,得出:
\lim_{x\to 0}\frac{\sin{x}}{x}=1
\end{align}
\]
