导数
一个函数的导数可以大致理解为:该函数在某处的切线的斜率(slope),或者说,某点附近的曲线的变化率
定义
设函数\(y=f(x)在点x_{0}\)的某一邻域内有定义,当自变量\(x在x_{0}\)处取得增量\(\Delta x(点 x_{0}+\Delta x仍在该邻域内)时,\) 相应地因变量取得增量\(\Delta y=f(x_{0}+\Delta x)-f(x_{0}),\)
如果极限:
\[\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}= \lim_{\Delta x \to 0}\frac{f(x_{0}+\Delta x)-f(x_{0})}
{\Delta x}
\]
存在,则称函数\(y=f(x)\)在点\(x_{0}\)处可导, 并称该极限值为函数\(y=f(x)\)在点\(x_{0}\)处的导数.记作: \(f'(x_{0}).\)
\[\\ \\
\]
\[即: \enspace f'(x_{0})=\lim_{\Delta x \to 0}\frac{f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}
\]
\[\\ \\
\]
\[或: \enspace y' |\left. x=x_{0},\frac{dy}{dx} \right|
\\
或: \enspace y' |\left. x=x_{0},\frac{df(x)}{dx} \right|
\]
几何意义
设 \(y=f(x)\), 其函数如下图所示
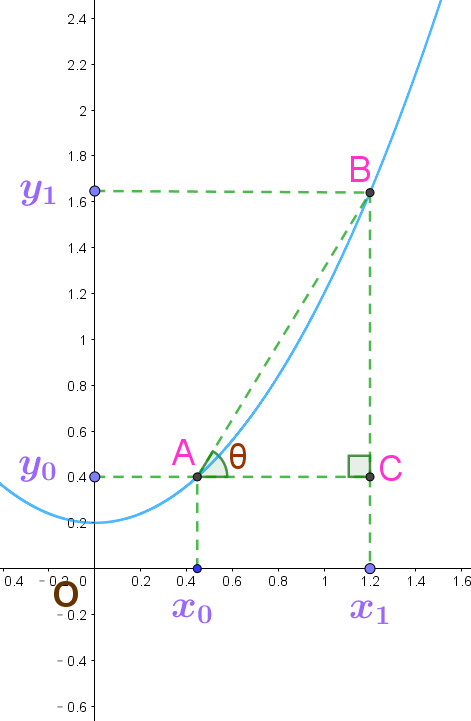
\[AB的斜率= \frac{BC}{AC} = \frac {y_{1}-y_{0} } {x_{1}-x_{0} }= \tan{\theta}
\]
\(\tan{\theta}=\frac {y_{1}-y_{0} } {x_{1}-x_{0} }= \frac{Δy} {Δx}, \quad Δy = y_{0}\) 至\(y_{1}\)之间的距离(distance), \(Δx = x_{0} 至x_{1}之间的距离,\)
当\(B\)点沿曲线下滑而不断趋近于\(A\)点时,\(AB\)斜率就越精确
\[\\ \\
\]
\[\because y_{1}=f(x_{0}+Δx),\quad y_{0}=f(x_{0})\]
\[\\ \\
\]
\[\therefore
\lim_{Δx\to 0}\frac{Δy}{Δx}=
\lim_{Δx\to 0}\frac{f(x_{0}+Δx)-f(x_{0})}{Δx}
=\frac{dy}{dx}
=\tan{\theta}
\]
\[\\ \\
\]
求\(f(x)\)的导数\(f'(x)\), 在这里可近似地认为是在求\(AB\)的斜率, 即求\(\tan{\theta}\)
