证明几何平均值小于等于算术平均值
方法一,采用数学归纳法,证明几何平均值小于等于算术平均值
\[\\
即:
\sqrt[n]{ a_{1} \cdot a_{2}\cdot ... \cdot a_{n}}
\ll
\frac{a_{1}+a_{2}+...+a_{n}}{n} ,
n \in N
\\
于此设n=2,令算术平均值-几何平均值,则得:\\
\frac{a_{1}+a_{2}}{2} -
\sqrt[2]{ a_{1} \cdot a_{2}}
\\
\Rightarrow
\frac{a_{1}^2+2a_{1}a_{2}+a_{2}^2}{4}-
a_{1}a_{2}
\\
\Rightarrow
\frac{a_{1}^2+2a_{1}a_{2}+a_{2}^2-4a_{1}a_{2}}{4}
\\
\Rightarrow
\frac{(a_{1}-a_{2})^{2}}{4}
\\
\because \frac{(a_{1}-a_{2})^{2}}{4} \gg 0
\\
\therefore
\frac{a_{1}+a_{2}}{2}
\gg
\sqrt[2]{ a_{1} \cdot a_{2}}
\\
证明成立
\]
方法二: 几何法证明
如图:
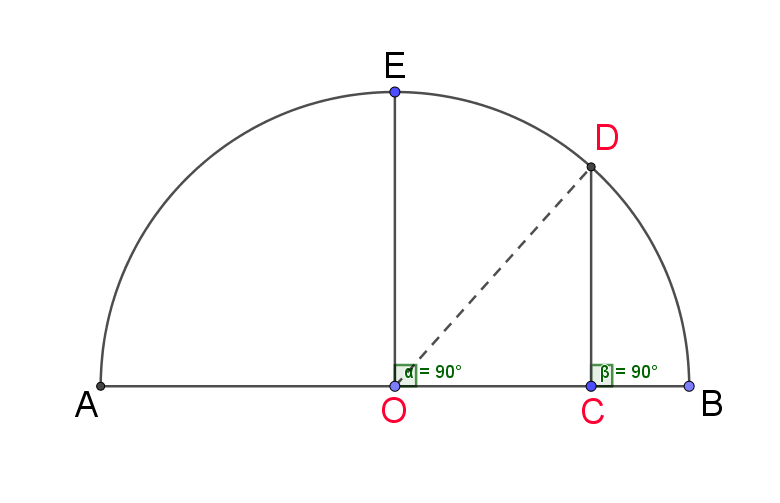
- O点为圆心点,D和E为半圆圆周上的点
- EO垂直于AB于点O,DC平行于EO
- DC与AB相交于点C
- D点能在半圆圆周上滑动位置,C点位置也会随D点的移动在AB上进行变动
- 但DC永远与EO平行,即永远垂直于AB
\[\\ \\
\]
设AC=a,BC=b
\[\\ \\
\]
\[\because OA=OB=OD=\frac{a+b}{2},即r\\
OC=OB-BC= \frac{a+b}{2}-b=\frac{a-b}{2} \]
\[\\ \\
\]
\[\therefore CD=\sqrt[]{OD^{2}-OC^{2}} \\
=\sqrt[]{(\frac{a+b}{2})^{2} - (\frac{a-b}{2})^{2} } \\
=\sqrt[]{ab} \]
\[\\ \\
\]
\[ \because CD \ll r ,\quad
\therefore \sqrt[]{ab} \ll \frac{a+b}{2} \]
\[\\ \\
\]
因此几何平均值 小于等于 算术平均值
