三角函数
definition
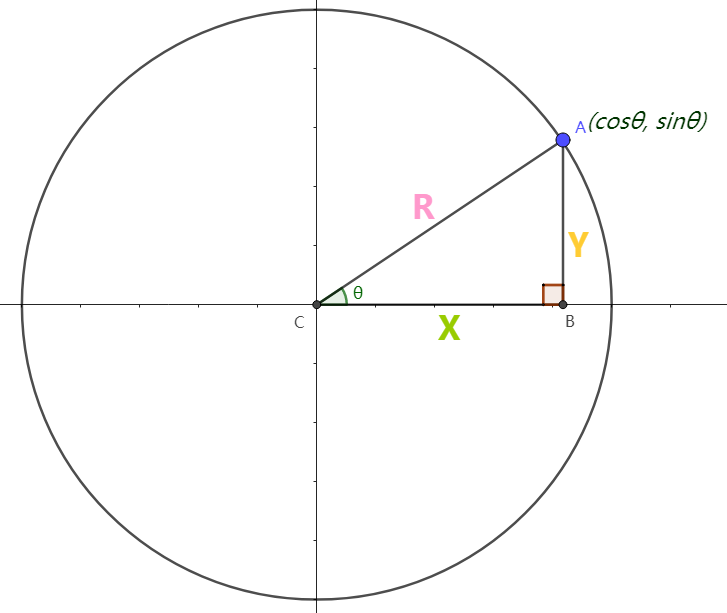
\[\begin{eqnarray}
正弦: \sin{θ}=\frac{y}{r}
\\ \\
余割: \csc{θ}=\frac{r}{y}
\\ \\ \\
余弦: \cos{θ}=\frac{x}{r}
\\ \\
正割: \sec{θ}=\frac{r}{x}
\\ \\ \\
正切: \tan{θ}=\frac{y}{x}
\\ \\
余切: \cot{θ}=\frac{x}{y}
\end{eqnarray}
\]
dynamic 0
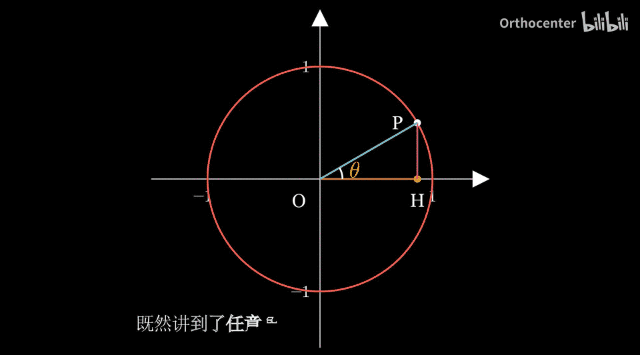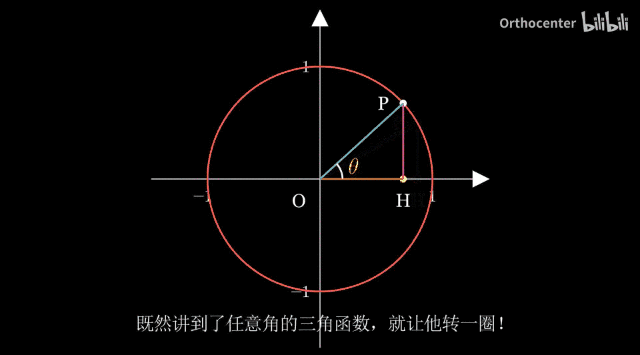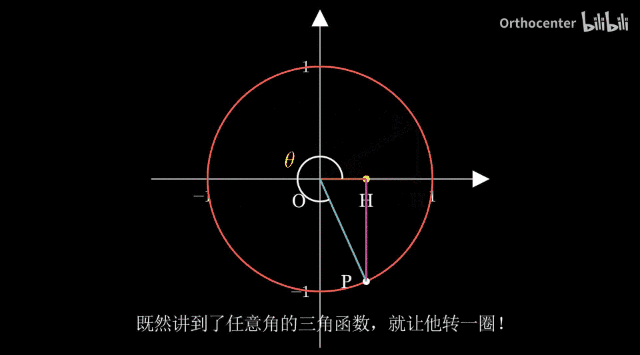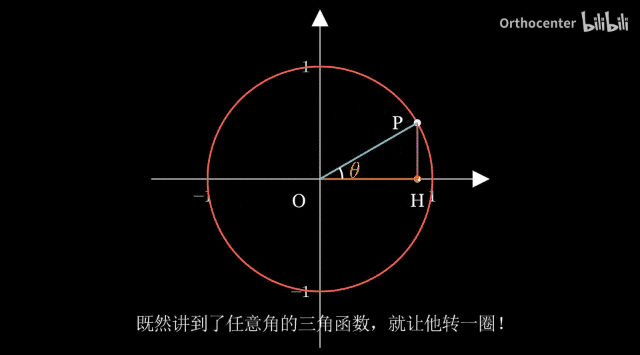
dynamic 1
preamble
函数的性质可以通过图像来直观的看出。
三角函数都是周期函数，因此三角函数的函数图像都是一段函数图像的循环。
例如\(\sin{x}\) 、\(\cos{x}\) 和 \(\tan{x}\)，它们都以 \(2\pi\) 为周期，如:
\[\sin{(x+2\pi)}=\sin{(x)}
\]
正弦函数\(\sin{x}\)和余弦函数\(\cos{x}\)的图像形状差不多，左右移动适当距离，就能使 \(\sin{x}\) 和 \(\cos{x}\) 的函数图像重合。
\(\tan{x}\) 在 \(\frac{\pi}{2}\) 时的函数值是不存在的，因为推导如下:
\[\begin{eqnarray}
\tan{x} = \frac{\sin{x}}{\cos{x}}
\\ \\
\cos{x}是分母,它不能等于0
\\ \\
但\cos{(\frac{\pi}{2})} = 0
\\ \\
\lim_{x\to \frac{\pi}{2}}{\sin{x}}=1
\\ \\
\lim_{x\to \frac{\pi}{2}}{\cos{x}}=0
\\ \\
\therefore \lim_{x \to \frac{\pi}{2}}{\tan{x}} = +\infty
\end{eqnarray}
\]
correspond
| \(\sin{x}\) | \(\cos{x}\) | \(\tan{x}\) | |
|---|---|---|---|
| 30° \((\frac{\pi}{6})\) | \(\frac{1}{2}\) | \(\frac{\sqrt[]{3}}{2}\) | \(\frac{\sqrt[]{3}}{3}\) |
| 45° \((\frac{\pi}{4})\) | \(\frac{\sqrt[]{2}}{2}\) | \(\frac{\sqrt[]{2}}{2}\) | 1 |
| 60° \((\frac{\pi}{3})\) | \(\frac{\sqrt[]{3}}{2}\) | \(\frac{1}{2}\) | \(\sqrt[]{3}\) |
| 90° \((\frac{\pi}{2})\) | 1 | 0 | \(+\infty\) 或不存在 |
| 180° \((\pi)\) | 0 | -1 | 0 |
| 270° \((\frac{3\pi}{2})\) | -1 | 0 | \(-\infty\) 或不存在 |
| 360° \((2\pi)\) | 0 | 1 | 0 |
