NOIP2018提高组模拟9.18
【jzoj 5872】小 A 的任务
Description
Input
Output
Sample Input
3
1 2 3
Sample Output
624
3
Data Constraint
对于 10%的数据,保证 $ n< 5 $
对于 40%的数据,保证 $ n<10 $
对于 70%的数据,保证 $ n<500 $
对于 100%的数据,保证 $ n \le 10^7, 1 \le s_i \le n $
题解
方法1:枚举每个任务选择,再枚举所有的三元组。
期望得分40
方法2:可以发现展开
后得到
根据排序不等式,顺序和 $ \ge $ 乱序和,重新整理后可得到
那么可以知道,任务一定是都要选,这样才能最大化优美程度。
期望得分65
方法3:注意到排序不等式的取等号条件,可以发现当所有都相同是无论是否选择任务优美程度都不会改变,
在最大化优美程度的基础上最小化选择的个数,此时所有的任务都不选择。
结合方法2,期望得分70
方法4:注意到统计的是所有的三元组,考虑分步计算贡献。由展开后的式子分为两部分进行计算
令 $ sum = \sum_{i=1}^n s_i , inv_{sum} = \sum_{i=1}^n \frac{1}{s_i}, sqr_{sum} = \sum_{i=1}^n s_i^2 $
容易得到 $ Ans=3 \times n^2 \times sum + 6 \times n \times inv_{sum} \times sqr_{sum} $
注意到 $ s_i \le n $ 所以可以 $ O(n) $ 预处理逆元后计算,复杂度 $ O(n) $ ,时限非常宽
结合方法3,期望得分100
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
#define ll long long
#define Mod 1000000007
ll read(){
char ch; ll x=0;
while(ch=getchar(),ch<'0'||ch>'9');x=ch-48;
while(ch=getchar(),ch>='0'&&ch<='9')x=10*x+ch-48;
return x;
}
int n;
ll s[10000005],sum1,sum2,sum3,ans;
ll qpow(ll x,ll k){
ll res=1;
while(k>0){
if(k&1) res=res*x%Mod;
x=x*x%Mod;
k>>=1;
}
return res%Mod;
}
signed main(){
freopen("problem.in","r",stdin);
freopen("problem.out","w",stdout);
scanf("%d",&n); bool f=1; int pre=-1;
for(int i=1;i<=n;++i){
s[i]=read();
sum1=(sum1+s[i])%Mod;
sum2=(sum2+s[i]*s[i]%Mod)%Mod;
sum3=(sum3+qpow(s[i],Mod-2))%Mod;
if(i>1&&pre!=s[i]) f=0;
pre=s[i];
}
ans=(3*n%Mod*n%Mod*sum1%Mod+6*n%Mod*sum2%Mod*sum3%Mod)%Mod;
printf("%lld\n",ans);
if(!f) printf("%d",n); else puts("0");
return 0;
}
【jzoj 5873】小p的属性
Description
Input
输入包括两行
第一行两个整数 $ n, m $
接下来 $ n $ 行,每行三个整数 $ x_i, y_i, z_i $
Output
输出包括一行
输出一个整数表示答案
Sample Input
2 4
2 1 10
1 2 20
Sample Output
50
Data Constraint
题解
方法1:枚举每天升级哪一种属性
期望得分20
方法2:注意到 $ n \le 10 $ ,考虑建立矩阵?,然后矩阵快速幂
期望得分40
方法3:注意到 $ m \le 1000 $ ,考虑 $ dp $ ,
$ dp[I][j] $ 表示前 $ i $ 天, $ a $ 属性到 $ j $ 的最大得分, 简单转移即可
结合方法2,期望得分60
方法4:注意到 $ x_i, y_i \le 1000 $ ,考虑前 $ 2000 $ 后每一天一定可以得到每一个奖励的分数,
前2000天 $ dp $ 转移,之后 $ O(1) $ 计算即可
结合方法2,期望得分80
方法5:注意到许多 $ dp $ 状态是无用的,且两个有用的 $ dp $ 状态之间可以 $ O(1) $ 转移,
考虑类似离散化的思想,只关心 $ dp $ 状态表示的 $ (a, b) $ 为某一个奖励的 $ (x_i, y_i ) $ ,转移即可
复杂度 $ O(n^2) $ ,期望得分100
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
#define ll long long
int read(){
char ch; int x=0;
while(ch=getchar(),ch<'0'||ch>'9');x=ch-48;
while(ch=getchar(),ch>='0'&&ch<='9')x=10*x+ch-48;
return x;
}
struct node{ int x,y,z; }a[1005],b[1005];
bool cmp1(node x,node y){ return x.x<y.x; }
bool cmp2(node x,node y){ return x.y<y.y; }
int n,m;
ll f[1005][1005],g[1005][1005],ans;
int main(){
freopen("growth.in","r",stdin);
freopen("growth.out","w",stdout);
n=read(); m=read();
for(int i=1;i<=n;++i){
a[i].x=read(); a[i].y=read(); a[i].z=read();
b[i]=a[i];
}
sort(a+1,a+1+n,cmp1);
sort(b+1,b+1+n,cmp2);
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j){
int x=a[i].x,y=b[j].y;
if(x+y>m) break;
if(b[j].x<=x) g[i][j]=g[i][j-1]+b[j].z;
else g[i][j]=g[i][j-1];
f[i][j]=max(f[i-1][j]+g[i-1][j]*(x-a[i-1].x-1),f[i][j-1]+g[i][j-1]*(y-b[j-1].y-1))+g[i][j];
ans=max(ans,g[i][j]*(m-x-y)+f[i][j]);
}
printf("%lld",ans);
return 0;
}





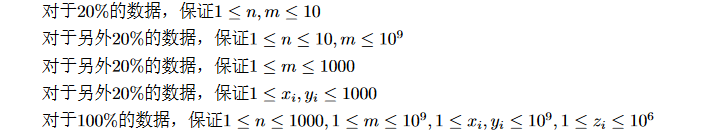

 浙公网安备 33010602011771号
浙公网安备 33010602011771号