Test 2018-09-19
| 题目名称 | 疯狂生长 | 两极反转 | 地震 | roads |
|---|---|---|---|---|
| 英文代号 | rooftrellen | magnus | crixalis | roads |
| 时限 | 1 秒 | 1 秒 | 见题面 | 1 秒 |
| 输入文件 | rooftrellen.in | magnus.in | crixalis.in | roads.in |
| 输出文件 | rooftrellen.out | magnus.out | crixalis.out | roads.out |
| 内存限制 | 512MB | 512MB | 512MB | 512MB |
注意:
本次测试中,选手在读入数据时会要求读入一个数据编号,方便选手对于不同的数据设计不同的算法,
而每个编号对应的数据范围也将在【数据规模和约定】 中体现。
而样例输入中的数据编号的作用仅仅是提醒选手不要忘了读入编号,并不代表这个编号对应的数据就是样例。
疯狂生长
【问题背景】
在 Rooftrellen 周围召唤出疯狂生长的伤害性藤条和枝干,阻止被缠绕的敌人移动、闪烁、进入隐身或攻击。
【问题描述】
树精世界里有 $ n $ 颗藤蔓,每颗藤蔓都有一个高度 $ h_i $ 。
Rooftrellen 可以耗费一个单位的能量把任意一颗藤蔓拔高 $ 1 $ 个单位长度。
他想知道,能否恰好耗 费自身现有的 $ m $ 个单位的能量,使得藤蔓都变得一样高?
【输入格式】
第一行一个整数 ID,表示数据的编号。
第二行一个整数 T, 表示数据的组数。 接下来有 T 组数据。
对于每组数据:
第一行两个整数 $ n, m $ ,表示藤蔓的数量和能量值。
第二行 n 个整数 $ h_1, h_2, …, h_n $ ,表示藤蔓的初始高度。
【输出格式】
对于每组数据: 一行一个字符串 Yes 或 No,表示答案。
【样例输入】
5 3
5 6
1 2 3 3 4
5 7
1 2 3 3 4
5 8
1 2 3 3 4
【样例输出】
No
Yes
No
【数据规模和约定】

对于100%的数据, $ h_i≤10^9 $ 。
【样例说明】
样例一,样例三:没有可行的方法。 样例二:从左到右依次增加 3,2,1,1,0 个单位长度即可。
【提示】
1、注意题面中的“恰好”。
2、 注意区别 ID 和 T。
题解
-
显然的贪心,先把所有藤蔓的高度都提到和最高的藤蔓一样高
(因为题目要求必须一样高而且不能让它们下降)
然后看所得消耗与 $ m $ 的大小关系。 -
如果所得消耗比 $ m $ 大,那么答案一定是No
如果所得消耗大于等于 $ m $ ,设所得消耗为 $ sum $ ,判断 $ (m-sum) $ % $ n $ 是否等于 $ 0 $
(这个时候所有藤蔓一样高,还是要保持一样高一定要让它们都再 $ +1 $ )
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int ID,T,n,m,h[105],maxh,res;
int main(){
freopen("rooftrellen.in","r",stdin);
freopen("rooftrellen.out","w",stdout);
scanf("%d %d",&ID,&T);
while(T--){
scanf("%d %d",&n,&m); maxh=-1; res=0;
for(int i=1;i<=n;++i){ scanf("%d",&h[i]); maxh=max(maxh,h[i]); }
for(int i=1;i<=n;++i) res+=maxh-h[i];
if(res==m) puts("Yes");
else if(res<m&&(m-res)%n==0) puts("Yes");
else if(res>m||(m-res)%n!=0) puts("No");
}
return 0;
}
两极反转
【问题背景】
Magnus 改变物质的属性,将附近的敌人都拖拽到他的前方,并且以强力的 震击对他们造成伤害和眩晕。
【问题描述】
猛犸世界中的数据网可以抽象成一个包含 $ n $ 个点 $ m $ 条边的有向图。
由于编写防火墙的码农比较偷懒,因此数据网经常遭到攻击,某些边的方向会变化,使得数据无法在节点之间相互传递。
这时 Magnus 的能力就起作用了,他 可以耗费 $ 1 $ 单位的体力值来使任意一条边反向。
Magnus 想知道, 如果要把数据从节点 $ x_i $ 传输到节点 $ y_i $ ,他至少要耗费多少体力值呢?
【输入格式】
第一行一个整数 ID,表示数据的编号。
第二行三个整数 $ n, m, q,$ 表示有向图的点数,边数和询问数。
接下来 $ m $ 行,每行 2 个整数 $ x_i $ 和 $ y_i $ ,表示 $ x_i $ 和 $ y_i $ 之间有一条有向边。
接下来 $ q $ 行,每行 2 个整数 $ x_i $ 和 $ y_i $ ,表示一组询问。
【输出格式】
$ q $ 行,每行一个正整数,表示至少耗费的体力值。 如果无法传输,输出-1。
【样例输入一】
1
8 7 1
1 2
3 2
3 4
7 4
6 2
5 6
7 5
1 7
【样例输出一】
2
【样例输入二】
1
8 7 1
1 2
3 2
3 4
7 4
6 2
5 6
7 5
1 8
【样例输出二】
-1
【样例说明】
对于样例一,只要将 $ 3 \rightarrow 2 $ 和 $ 7 \rightarrow 4 $ 两条边反向即可。
对于样例二,节点 8 的入度和出度均为 0,所以无法传输。
【数据规模和约定】

【提示】
1、注意题面中的“如果”,每次询问并不会真的将某些边反向。
题解
-
此题考虑数据分治
-
对于前14个点,由于 $ q=1 $ ,我们考虑建图,
对于有向边 $ (u,v) $ ,我们存一条 $ u \rightarrow v \quad cost: 0 $ 的边,
对于它的反向边,我们存一条 $ v \rightarrow u \quad cost: 1 $ 的边,
使 $ x $ 作为源点跑一遍 $ SPFA $ 即可。 -
对于后面的数据,由于题目保证是一棵树,考虑 $ LCA $ 和前缀和。
除了 $ dep $ ,我们多维护一个信息 $ dis $ 代表 $ 1 $ 节点到当前节点需要走多少条反向边,
还是像之前一样建边,然后维护即可。
最后计算答案的时候,由于 $ x $ 点要往上走,它的反向边与 $ 1 $ 到它的反向边意义正好相反,我们要用 $ dep - dis $ 得到正确的反向边数量 -
对于一对 $ x_i,y_i $ ,它们的答案即为 $ ans=dep_x-dis_x+dis_y-dep_{lca} $
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
int ID,n,m,q;
struct edge{ int v,w,nxt; }e[100005<<2];
int head[100005],tot;
inline void add(int u,int v,int w){ e[++tot].v=v; e[tot].w=w; e[tot].nxt=head[u]; head[u]=tot; }
int dis[100005];
bool vis[100005];
inline void spfa(int s){
for(int i=1;i<=n;++i) dis[i]=0x3f3f3f3f;
queue<int>q; q.push(s); dis[s]=0;
while(!q.empty()){
int u=q.front(); vis[u]=0; q.pop();
for(int i=head[u];i;i=e[i].nxt)
if(dis[e[i].v]>dis[u]+e[i].w){
dis[e[i].v]=dis[u]+e[i].w;
if(!vis[e[i].v]){ vis[e[i].v]=1; q.push(e[i].v); }
}
}
}
int dep[100005],f[100005][21];
void dfs(int u,int fa){
dep[u]=dep[fa]+1; f[u][0]=fa;
for(int j=1;j<=20;++j)
f[u][j]=f[f[u][j-1]][j-1];
for(int i=head[u];i;i=e[i].nxt){
if(e[i].v==fa) continue;
dis[e[i].v]=dis[u]+e[i].w;
dfs(e[i].v,u);
}
}
inline int lca(int u,int v){
if(dep[u]>dep[v]) swap(u,v);
for(int i=20;~i;--i)
if(dep[u]<=dep[v]-(1<<i)) v=f[v][i];
if(u==v) return u;
for(int i=20;~i;--i)
if(f[u][i]!=f[v][i]){ u=f[u][i]; v=f[v][i]; }
return f[u][0];
}
signed main(){
freopen("magnus.in","r",stdin);
freopen("magnus.out","w",stdout);
scanf("%d",&ID);
scanf("%d %d %d",&n,&m,&q);
if(q==1){
for(int i=1;i<=m;++i){
int u,v;
scanf("%d %d",&u,&v);
add(u,v,0); add(v,u,1);
}
int x,y;
scanf("%d %d",&x,&y);
spfa(x);
if(dis[y]==0x3f3f3f3f) puts("-1");
else printf("%d",dis[y]);
} else {
for(int i=1;i<=m;++i){
int u,v;
scanf("%d %d",&u,&v);
add(u,v,0); add(v,u,1);
}
dfs(1,0);
while(q--){
int x,y;
scanf("%d %d",&x,&y);
int Lca=lca(x,y);
printf("%d\n",(dep[x]-dis[x])+dis[y]-dep[Lca]);
}
}
return 0;
}
地震
【问题背景】
持续施法 - 在 2 秒吟唱后, Crixalis 向地中发送扰动,引起大地剧烈震动。
所有范围内的敌人会受到伤害并被减速。每次后续震击都会提高伤害传播 半径。可用神杖升级。
【问题描述】
Crixalis 平日很喜欢捣乱,这导致沙尘世界每隔一个小时就有一次地震发生。
沙尘世界所有的 $ n $ 幢建筑都在一条直线上,从左到右依次标号为 $ 1~n $ 。
每次地震由三个参数决定:受影响的建筑区间 $ [L_i, R_i] $ 以及地震的强度 $ F_i $ 。
任意时刻每幢建筑物都有一个高度, 用一个数字串来表示(可能含有前导 0)。
每一次地震来临时,受影响建筑的高度数字串将根据地震的强度向左旋转相应的位数, 但是不要忘了前导零的存在,
举个例子:高度串是 120 的建筑连续受到 三次强度为 1 的地震的影响之后,高度串分别变为 201, 012, 120。
沙尘世界的守卫想出了一个保护建筑的方法,但有时需要知道某个区间内最高的建筑的高度。
现在给出了这 $ n $ 幢建筑初始的高度数字串,以及有以下两种操作:
1、 U Li Ri Fi,表示 $ [L_i, R_i] $ 区间内的建筑受到了强度为 Fi 的地震的影响。
2、 Q Li Ri,表示询问 $ [L_i, R_i] $ 区间内当前最高的建筑的高度。 你需要模拟这两种操作,帮助守卫解决问题。
【输入格式】
第一行一个整数 ID,表示数据的编号。
第二行两个整数 $ n, q $ , 表示建筑的数量和操作数。
第三行 $ n $ 个整数 $ a_1, a_2, …, a_n $ ,表示每幢建筑的初始高度串。
接下来 $ q $ 行,每行表示两种操作中的某一种。
【输出格式】
对于每个 Q 操作,输出一行一个整数,表示该操作的答案。
注意输出的整数不能包含前导 0。
【样例输入】
2
3 8
17 3140 832
Q 1 3
U 1 3 1
Q 2 3
Q 1 1
U 1 3 2
Q 1 3
U 2 2 1
Q 1 3
【样例输出】
3140
1403
71
832
3140
【数据规模和约定】
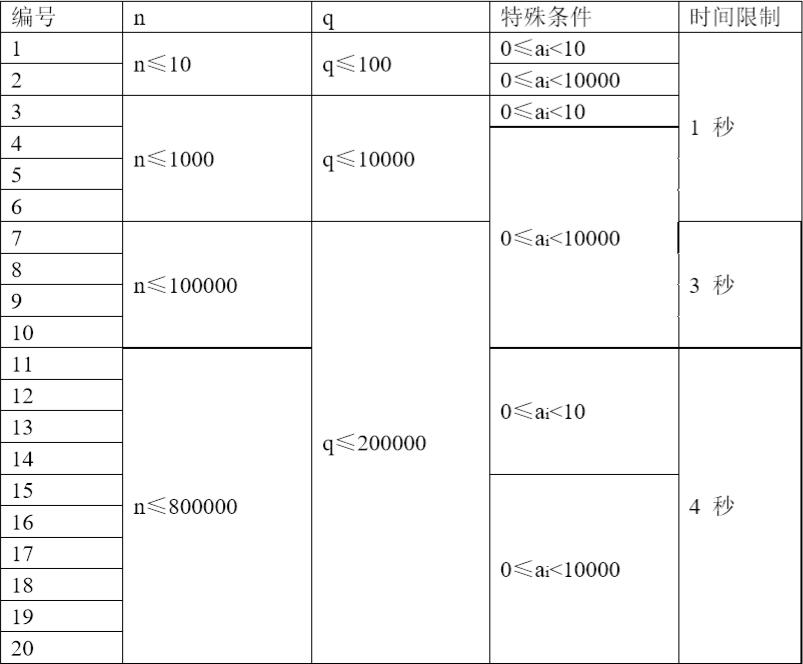
对于100%的数据,初始的高度数字串不包含前导 0, $ 1≤F_i≤60 $ 。
【样例说明】
第一次 U 操作之后=>[71, 1403, 328]
第二次 U 操作之后=>[71, 0314, 832]
第三次 U 操作之后=>[71, 3140, 832]
【提示】
1、 虽然是高度数字串,但是应看做数字来比较大小而不是字典序。例如:0123 和 122 比较, 0123 的高度较大。
2、注意本题特殊的时间限制
代码
- 线段树,我写挂了!题解的线段树指针满天飞,看看就好。(;´д`)ゞ
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <ctime>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <deque>
#include <set>
#include <map>
#define pb push_back
#define mp make_pair
#define LL long long
#define maxlongint 2147483647
using namespace std;
const int inf = 999999999;
const int mod = 1000000007;
const int MAXN = 800010;
const int MOD = 95542721;
const int LEN = 12;
inline int Getint()
{
char ch = getchar();
while (ch < '0' || ch > '9') ch = getchar();
int ret = 0;
while (ch >= '0' && ch <= '9') ret = ret * 10 + ch - '0', ch = getchar();
return ret;
}
int label;
inline void GetLabel()
{
freopen("crixalis.in", "r", stdin);
freopen("crixalis.out", "w", stdout);
label = Getint();
}
struct node
{
node *Lc, *Rc;
int v[LEN];
int L, R, m, p;
node (int x, int y)
{
L = x, R = y, m = L + R >> 1;
p = 0, Lc = Rc = 0;
memset(v, 0, sizeof(v));
}
};
node *root;
int a[MAXN], tmp[LEN], dig[10];
char ch[3];
int n, m, x, y, z;
inline int Mod(int x, int MOD)
{
while (x >= MOD) x -= MOD;
return x;
}
inline void Update(node *it)
{
for (int i = 0; i < LEN; i++)
{
it -> v[i] = max(it -> Lc -> v[i], it -> Rc -> v[i]);
}
}
inline void Clear(node *it)
{
if (!it -> p) return;
memcpy(tmp, it -> Lc -> v, sizeof(tmp));
for (int i = 0; i < LEN; i++)
{
it -> Lc -> v[i] = tmp[Mod(i + it -> p, LEN)];
}
it -> Lc -> p = Mod(it -> Lc -> p + it -> p, LEN);
memcpy(tmp, it -> Rc -> v, sizeof(tmp));
for (int i = 0; i < LEN; i++)
{
it -> Rc -> v[i] = tmp[Mod(i + it -> p, LEN)];
}
it -> Rc -> p = Mod(it -> Rc -> p + it -> p, LEN);
it -> p = 0;
}
node *Build(int L, int R)
{
node *it = new node(L, R);
if (L < R)
{
it -> Lc = Build(L, it -> m);
it -> Rc = Build(it -> m + 1, R);
Update(it);
}
else
{
int t = a[L], L0 = 0;
while (t)
{
dig[++L0] = t % 10;
t /= 10;
}
int start = L0;
for (int i = 0; i < LEN; i++)
{
int now = 0;
for (int j = start; j > 0; j--) now = now * 10 + dig[j];
for (int j = L0; j > start; j--) now = now * 10 + dig[j];
it -> v[i] = now;
start--;
if (!start) start = L0;
}
}
return it;
}
int Query(node *it, int L, int R)
{
if (it -> L == L && it -> R == R) return it -> v[0];
Clear(it);
if (R <= it -> m) return Query(it -> Lc, L, R);
if (L > it -> m) return Query(it -> Rc, L, R);
return max(Query(it -> Lc, L, it -> m), Query(it -> Rc, it -> m + 1, R));
}
void Modify(node *it, int L, int R, int level)
{
if (it -> L == L && it -> R == R)
{
it -> p += level;
memcpy(tmp, it -> v, sizeof(tmp));
for (int i = 0; i < LEN; i++)
{
it -> v[i] = tmp[Mod(i + level, LEN)];
}
return;
}
Clear(it);
if (R <= it -> m)
{
Modify(it -> Lc, L, R, level);
}
else if (L > it -> m)
{
Modify(it -> Rc, L, R, level);
}
else
{
Modify(it -> Lc, L, it -> m, level);
Modify(it -> Rc, it -> m + 1, R, level);
}
Update(it);
}
inline void Init()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
}
root = Build(1, n);
}
inline void Work()
{
for (int i = 1; i <= m; i++)
{
scanf("%s%d%d", ch, &x, &y);
if (ch[0] == 'Q')
{
printf("%d\n", Query(root, x, y));
}
else
{
scanf("%d", &z);
Modify(root, x, y, z);
}
}
}
int main()
{
GetLabel();
Init();
Work();
return 0;
}
Paid Roads
【题目描述】
这里有一个地图,嗯~准确的说是一个藏宝图。
你在 $ 1 $ 号点,宝藏在 $ n $ 号点, 所有的点编号 $ 1~n $ ,
这块宝底的地形是很奇怪的,每两个点之间有两条通路,两 个通路的长度是不一样的,可能会有一条比较短,你可以任选一条,
但是其中一 条你只有在之前经过某个点的时才能通行,就好像这条路的通行证在那个点上一 样。
现在想知道怎么样走才能以最短的路程到达藏宝点。
【输入格式】
第一行两个用空格隔开的整数 $ n $ 和 $ m $ 分别表示节点的编号个数和该藏宝点路径条数。
第二行到第 $ m + 1 $ 行每行 5 个整数 $ a,b,c,la,lb $ 描述从 $ a $ 点到 $ b $ 点的有向路,
$ la $ 表示之前经过 $ c $ 后,可以从 $ a $ 到 $ b $ 的路径长度,
$ lb $ 表示随时都可以通行的 $ a $ 到 $ b $ 的路径长度。
【输出格式】
一行一个整数表示的是从 $ 1 $ 到 $ n $ 的最短路程。如果没有路输出“ impossible”。
【输入样例】
4 5
1 2 1 10 10
2 3 1 30 50
3 4 3 80 80
2 1 2 10 10
1 3 2 10 50
【输出样例】
110
【数据范围】
$ n,m ≤ 10 $
$ la,lb ≤ (2<<31)-1 $
代码
- 为什么没有题解?这么小的数据直接分层图最短路就可以了( ̄y▽, ̄)╭
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
struct edge{ int v,c,w1,w2,nxt; }e[11];
int head[11],cnt;
inline void add(int u,int v,int c,int w2,int w1){
e[++cnt].v=v; e[cnt].c=(1<<c-1);
e[cnt].w1=w1; e[cnt].w2=w2;
e[cnt].nxt=head[u]; head[u]=cnt;
}
int n,m,tot,dis1[11],dis2[11],prei[11],nowi[11],nxti[11];
bool vis[11][1ll<<11];
unsigned long long dis[11][1ll<<11];
void spfa(){
queue<int>q; queue<unsigned long long>p;
q.push(1); p.push((1ll<<1-1)); dis[1][1ll<<1-1]=0;
while(!q.empty()){
int u=q.front(); q.pop();
unsigned long long P=p.front(); p.pop(); vis[u][P]=0;
for(int i=head[u];i;i=e[i].nxt){
if(P&e[i].c)
if(dis[e[i].v][P|(1ll<<e[i].v-1)]>dis[u][P]+e[i].w2){
dis[e[i].v][P|(1ll<<e[i].v-1)]=dis[u][P]+e[i].w2;
if(!vis[e[i].v][P|(1ll<<e[i].v-1)]){
vis[e[i].v][P|(1ll<<e[i].v-1)]=1;
q.push(e[i].v); p.push(P|(1ll<<e[i].v-1));
}
}
if(dis[e[i].v][P|(1ll<<e[i].v-1)]>dis[u][P]+e[i].w1){
dis[e[i].v][P|(1ll<<e[i].v-1)]=dis[u][P]+e[i].w1;
if(!vis[e[i].v][P|(1ll<<e[i].v-1)]){
vis[e[i].v][P|(1ll<<e[i].v-1)]=1;
q.push(e[i].v); p.push(P|(1ll<<e[i].v-1));
}
}
}
}
}
int main(){
freopen("roads.in","r",stdin);
freopen("roads.out","w",stdout);
scanf("%d %d",&n,&m);
tot=(1<<n)-1;
for(int i=1;i<=m;++i){
int a,b,c,la,lb;
scanf("%d %d %d %d %d",&a,&b,&c,&la,&lb);
add(a,b,c,la,lb);
}
for(int i=1;i<=n;++i)
for(int j=1;j<=tot;++j)
dis[i][j]=(2ll<<31)-1;
spfa();
unsigned long long ans=(2ll<<31)-1;
for(int i=1;i<=tot;++i) ans=min(ans,dis[n][i]);
if(ans==((2ll<<31)-1)) puts("impossible");
else printf("%lld",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号