图论
博客迁移计划19
邻接矩阵
-
记录边权的邻接矩阵
-
二维矩阵 $ D[i,j]= \underbrace{\overbrace{ w(i,j),(i,j)-\in E }^{+ \infty,(i,j) \not\in E}}_{ 0,i=j } ,O(n^2),E $ 表示边集,注意重边
-
只记录联通情况的邻接矩阵
-
二维数组 $ A[i,j]= \underbrace{\overbrace{ 1,(i,j)\in E }^{0,(i,j)\not\in E}}_{ 0,i=j } ,O(n^2) $
A^k
- 就是矩阵乘法
- 邻接矩阵的次幂 $ A^k $ 的元素 $ (A^k)_{I,j} $ 表示 $ i $ 到 $ j $ 长度恰好为 $ k $ 的路径条数,
例题
-
GCJ2018 R3 B
-
由于GCJ是谷歌程序设计大赛,只好阉割掉此例题。
D^k ?
- 一般食用方法:
例题
传递闭包
- 以 $ or $ 为加法,$ ans $ 为乘法
- $ n $ 个点传递闭包的结果矩阵就是
- $ O(n^4) $,本质上是以路径长度为“阶段“的动态规划
传递闭包 - Floyd
-
考虑以图的规模为“阶段”进行递推
-
比较 $ C(n) $ 与 $ C(n-1) $
-
$ 1. $ 多了第 $ n $ 行和第 $ n $ 列
-
$ 2. $ 前 $ n-1 $ 行 $ n-1 $ 列多了中转点 $ n $
-
设 $ F[p,i,j] $ 表示在“中途只经过编号 $ \le p $ 的点”的前提下 $ i $ 到 $ j (1 \le i,j \le n ) $ 的可达性
- $ O(n^3) $,空间上 $ p $ 这一维可以省略
最短路 - Floyd
- 设 $ F[p,i,j] $ 表示在”中途只经过编号 $ \le p $ 的点“的前提下 $ i $ 到 $ j (1 \le i,j \le n ) $ 的最短路
- $ O(n^3) $,空间上 $ p $ 这一维可以省略
-
推广:
-
统计路径条数
-
无向图最小环
邻接表
-
表头数组 $ head[N] $ ,指向从某点出发的第 $ 1 $ 条边
-
边集大小 $ tot $
-
边集数组 $ ver[M] \quad edge[M] \quad next[M] $
-
无向边看作一对方向相反的有向边,按照有向边储存
-
$ C++ \quad vector $ 大法
遍历
树
先/中/后序,$ DFS 序^{这玩意超级有用} $ ,欧拉序
图
$ DFS $ :求出 $ 搜索树^{炒鸡有用 \times 2} $ 、找出联通快
$ BFS $ :分层、$ 拓扑序^{再加个鸡腿 \times 3} $
例题
树的直径
-
给定一颗树,树中每条边都有一个权值
-
树中两点之间的距离定义为连接两点的路径上的边权之和。
-
树中最远的两个节点之间的距离被称为树的直径
-
连接这两点的路径被称为树的最长链
-
两种求法,均为 $ O(n) $
-
两次 $ DFS $ 或 $ BFS $
-
树形 $ DP $
图的直径
-
在一张无向图中,两个点 $ x,y $ 之间的距离定义为 $ x,y $ 的最短路长度
-
图中距离最远的两个点之间的最短路径称为图的直径
-
基环树的直径
-
每棵子树树形 $ DP $ ,环上单调队列优化 $ DP , O(N) $
-
仙人掌的直径
-
在深度优先遍历过程中
-
对每棵“子基环树”按照上述方法求直径,更新答案
-
然后把“子基环树”缩成一条“边”,长度为基环树的深度
例题
最短路
-
老生常谈的话题了
-
$ Dijstra / SPFA $ 什么的大家都会
-
三角形不等式
-
最短路、次短路条数
-
最短路径图
例题
负环
-
$ Bellman-Ford $
-
若经过 $ n $ 轮迭代,算法仍未结束(仍能产生更新的边),则图中存在负环。
-
若 $ n-1 $ 轮迭代之内,算法结束(所有边满足三角形不等式),则图中无负环。
-
$ SPFA $ 判定负环
-
记录每个点的最短路径包含的边数,超过 $ n $ 说明有负环
-
也可以卡内存、卡时间、爆了队列就判定有负环(雾 -
以及使用栈版本、$ DFS $ 版本
同余类BFS
最小生成树
-
依然老生常谈
-
$ Prim, Kruskal $ 什么的大家也都会......
-
次小生成树
-
根节点有度数限制的最小生成树(贪心法 $ or $ 二分法)
-
最小树形图(朱-刘算法)
-
不定根的最小树形图(虚拟根节点)
例题
最近公共祖先
-
给定一颗有根树
-
若节点 $ z $ 既是节点 $ x $ 的祖先,也是节点 $ y $ 的祖先,则称 $ z $ 是 $ x,y $ 的公共祖先
-
在 $ x,y $ 的所有公共祖先中,深度最大的一个称为 $ x,y $ 的最近公共祖先,记为 $ lca(x,y) $
-
三种求法:
-
直接标记法 $ O(nm) $
-
树上倍增法 $ O((n+m)log n) $
-
$ Tarjan $ 算法 $ O(n+m) $
-
基环树两点距离
-
分别对每棵子树倍增 $ LCA $
-
若查询时,倍增 $ x,y $ 在环上相遇,则对环的两侧长度取 $ min $
-
仙人掌两点距离
-
从 $ 1 $ 号点出发求单源最短路,得到 $ dist[x] $ 表示 $ 1 $ 到 $ x $ 的距离
-
从 $ 1 $ 号点出发 $ DFS $ ,对于每个环,断开所有环边,环上点直接连向环的“最高点”
-
对新得到的树构造倍增数组,查询 $ LCA $ 时
-
若对 $ x,y $ 倍增,最终不在环上相遇,则输出 $ dist[x]+dist[y]-2*dist[lca(x,y)] $
-
否则像基环树 $ LCA $ 一样,考虑环上的两种走法,取 $ min $
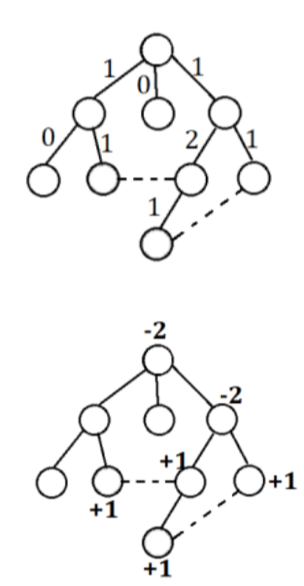
树上差分
-
给定一棵树,再给出若干条附加边
-
每条附加边 $ (x,y) $ 把树上从 $ x $ 到 $ y $ 的路径上的边覆盖了一次
-
求树上每条边被覆盖了多少次
-
对于每条附加边
-
$ x $ 处 $ +1 $
-
$ y $ 处 $ +1 $
-
$ lca(x,y) $ 处 $ -2 $
-
$ DFS $ 求子树和
例题
差分约束
-
差分约束系统是一种特殊的 $ N $ 元一次不等式组
-
$ N $ 个变量 $ X_i ~ X_N $
-
$ M $ 个约数条件,每个约束条件都是由两个变量作差构成的,形如 $ X_i - X_j \le c_k $
-
其中 $ c_k $ 是常数(可以是非负数,也可以是负数),$ 1 \le i,j \le N , 1 \le k \le M $
-
我们要解决的问题就是:
-
求一组解 $ X_1=a_1, X_2=a_2, \dots , X_N=a_N $ ,使所有约束条件都得到满足。
-
差分约束系统的每个约束条件 $ X_i - X_j \le c_k $ 可以变形为 $ X_i \le X_j + c_k $
-
与单源最短路问题中的三角形不等式 $ dist[y] \le dist[x]+z $ 非常相似。
-
可以把每个变量 $ X_i $ 看作 有向图中的一个节点 $ i $
-
对于每个约束条件 $ X_i - X_j \le c_k $ ,从节点 $ j $ 向节点 $ i $ 连一条长度为 $ c_k $ 的有向边
-
注意到如果 $ [a_1,a_2,\dots,a_N] $ 是一组解, 那么对于任意的常数 $ \Delta , \quad [a+1+\Delta,\dots,a_N+ \Delta] $
-
显然也是一组解,所以不妨假设 $ \forall i, \quad X_i \le 0 $
-
应该从节点 $ 0 $ 向每个节点 $ i $ 连一条长度为 $ 0 $ 的有向边
-
设 $ dist[0]=0 $
-
以 $ 0 $ 为起点求单源最短路
-
若图中存在负环,则给定的差分约束系统无解。
-
否则,$ X_i=dist[i] $ 就是差分约束系统的一组解。
- 约束条件形如 $ X_i- x_j \ge c_k $ 时,也可求单源最长路、判定是否存在“正环”
例题
欧拉路问题
-
俗称一笔画问题
-
若存在一条从 $ s $ 到 $ t $ 的路径,恰好经过无向图每条边一次,则称它为 $ s $ 到 $ t $ 的欧拉路。
-
若存在一条从 $ s $ 到 $ s $ 的路径,恰好经过无向图每条边一次,则称它为欧拉回路。
-
存在欧拉路 $ \Leftrightarrow $ 某两个点度数为奇数,其他点度数为偶数
-
存在欧拉回路 $ \Leftrightarrow $ 所有点度数都是偶数
欧拉回路求法
void dfs(int x)
对于从x出发的每条边(x,y)
如果该边没有被访问过
把这条边标记为已访问
dfs(y)
把y入栈
在主函数中
dfs(1)
倒序输出栈中所有节点
例题
连通分量
无向图连通性
-
给定无向联通图 $ G=(V,E) $;
-
若对于 $ x \in V $ ,从图中删去节点 $ x $ 以及所有与 $ x $ 关联的边之后,
$ G $ 分裂成两个或两个以上不相连的子图,则称 $ x $ 为 $ G $ 的割点。 -
若对于 $ e \in E $ ,从图中删去边 $ e $ 之后,
$ G $ 分裂成两个不相连的子图,则称 $ e $ 为 $ G $ 的桥或割边。 -
若一张无向联通图不存在割点,则称它为“点双联通图”。
-
若一张无向联通图不存在桥,则称它为“边双联通图”。
-
无向联通图的极大点双联通子图被称为“点双连通分量”,简记为“ $ v-DCC $ ”。
-
无向联通图的极大边双联通子图被称为“边双连通分量”,简记为“ $ e-DCC $ ”。
双联通图的充要条件
-
一张无向联通图是“点双联通图”,当且仅当满足下列两个条件之一:
-
图的顶点数不超过 $ 2 $ 。
-
图中任意两点都同时包含在至少一个简单环中。
-
其中”简单环“指的是不自交的环,也就是我们通常画出的环。
-
一张无向联通图是”边双联通图“,当且仅当:
-
任意一条边都包含在至少一个简单环中。
Tarjan算法
-
搜索树
-
时间戳 $ dfn $
-
追溯值 $ low[x] $ 定义为以下节点的时间戳的最小值:
-
$ subtree(x) $ 中的节点( $ subtree(x) $ 表示搜索树中以 $ x $ 为根的子树)
-
通过 $ 1 $ 条不在搜索树上的边,能够到达 $ subtree(x) $ 的节点。
-
对于每一条与 $ u $ 相连的边 $ (u,v) $
-
若搜索树上的 $ v $ 是 $ u $ 的子节点,更新 $ low[u]=min(low[u],low[v]) $
-
若 $ (u,v) $ 不是搜索树上的边,更新 $ low[u]=min(low[u],dfn[v]) $
割点与桥的判定
- 若 $ x $ 不是搜索树的根节点(深度优先遍历的起点),
则 $ x $ 是割点当且仅当搜索树上存在 $ x $ 的一个子节点 $ y $ ,满足:
- 若 $ x $ 是搜索树的根节点,则需要有至少两个子节点 $ y_1,y_2 $ 满足上述条件。
- 无向边 $ (x,y) $ 是桥,当且仅当搜索树上存在 $ x $ 的一个子节点 $ y $ ,满足:
- 需要特别注意重边的问题
双连通分量的计算
-
边双连通分量:
-
只需求出无向图中所有的桥,把桥都删掉后,无向图会成若干个连通块,
每一个连通块就是一个边双连通分量。
-
点双连通分量
-
需要在 $ Tarjan $ 算法的过程中维护一个栈,并按照如下方法维护栈中元素:
-
当一个节点第一次被访问时,把该节点入栈。
-
当割点判定法则中的条件 $ dfn[x] \le low[y] $ 成立时,无论 $ x $ 是否为根,都要从栈顶不断弹出节点,直至节点 $ y $ 被弹出。
被弹出的所有节点与节点 $ x $ 一起构成一个 $ v-DCC $ 。
强连通分量
-
在有向图 $ G $ 中,若对于每一对顶点 $ (x,y) $ ,都至少存在一条从 $ x $ 到 $ y $ 的路径,则称 $ G $ 是强连通图。
-
有向图的极大强连通子图,称为强连通分量 $ (SCC) $
-
流图(有根有向图)
-
搜索树
-
树枝边、前向边、后向边、横叉边
Tarjan算法
-
基于对图的深度优先遍历,维护一个栈 $ S $
-
递归进入节点 $ x $ 时把 $ x $ 入栈
-
从 $ x $ 回溯时判断栈中从栈顶到 $ x $ 的节点能否构成一个 $ SCC $
-
追溯值 $ low[x] $ 定义为 $ subtree(x) $ 通过一条有向边能够到达的最早栈中节点
-
对于每一条与 $ u $ 相连的边 $ (u,v) $
-
若搜索树上 $ v $ 是 $ u $ 的子节点,更新 $ low[u]=min(low[u], low[v]) $
-
否则,若 $ v $ 在栈中,更新 $ low[u]=min(low[u], dfn[v]) $
-
从 $ u $ 回溯前,若 $ dfn[u]=low[u] $ ,则栈中从栈顶到 $ u $ 的节点构成 $ SCC $
例题
2-SAT问题
-
能够解决如下的一般化模型
-
$ n $ 个变元,每个为真或假
-
若干个条件命题,形如“若 $ p $ 则 $ q $ ”
-
求满足所有条件的一种赋值
-
每个变元对应两个点
-
对于每个条件命题,产生 $ p \rightarrow q $ 和 $ q' \rightarrow p' $ 两条边,后者代表其逆否命题
-
存在满足条件的赋值 $ \Leftrightarrow $ 每个变元对应的两个点都不属于同一个强连通分量
-
赋值方法:$ val(x)=c[x]<c[x'], \quad c $ 为 $ tarjan $ 求出的 $ SCC $ 编号
例题
二分图
-
定义:
-
无向图,点可以分成两个集合,每个集合内部没有边
-
一张无向图是二分图,当且仅当图中不存在奇环
-
判定方法:
-
黑白染色,看是否有冲突
例题
二分图匹配
-
“任意两条边都没有公共端点”的边的集合称为图的匹配
-
最大匹配就是包含边的个数最多的匹配
-
设 $ M $ 是一个匹配,如果存在一条边连接两个未匹配顶点的路径 $ P $ ,
使得属于 $ M $ 的边和不属于 $ M $ 的边在 $ P $ 上交替出现,则称 $ P $ 是一条增广路(交错路)。

增广路的性质
-
路径的长度一定为奇数,第一条边和最后一条边一定不属于 $ P $
-
将 $ P $ 上所有的边关于 $ M $ 取反(匹配边与未匹配边交换),可以得到一个更大的匹配:

- 对于二分图最大匹配问题, $ M $ 为图 $ G $ 的最大匹配当且仅当找不到新的增广路
增广路算法
-
整体思想:
-
将匹配边集 $ M $ 置为空
-
寻找一条增广路径 $ P $ , $ P $ 上的边取反得到一个更大的匹配 $ M‘ $
-
重复上一步直到找不到增广路径为止
-
本质:贪心
-
实现方法:搜索(递归)
-
时间复杂度: $ O(|V| \times |E|) $
-
依次考虑每个左部未匹配点,寻找一个右部点与之匹配。
-
一个右部点能与之匹配,需要满足以下两个条件之一:
-
$ 1. $ 该点是未匹配点
此时直接把两个点进行匹配。 -
$ 2. $ 从与该节点匹配的左部点出发,可以找到另一个右部点与之匹配。
此时递归进入该左部点,为其寻找匹配的右部点。 -
利用访问标记避免重复搜索。
增广路算法演示

最小点覆盖
-
定义
-
一个点集,使得每条边至少有一个端点在集合中
-
$ K\ddot{o}nig $ 定理
-
二分图最小点覆盖的大小 $ = $ 二分图最大匹配集的大小

最大独立集
-
任意两点在图中都没有边相连的点集称为图的独立集
-
定理:二分图最大独立集 $ = $ 图的点数 $ - $ 二分图最大匹配
-
证明:选出最多的点构成独立集
-
$ \Leftrightarrow $ 在图中去掉最少的点,使剩下的点之间没有边。
-
$ \Leftrightarrow $ 用最少的点覆盖所有的边,去掉的是最小覆盖。
例题
-
GCJ 2018 R2 C
-
由于GCJ是谷歌程序设计大赛,只好阉割掉此例题。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号