1.1 教学计划与递归
1.1 教学计划与递归
由数据结构反推算法复杂度以及算法内容
作者: yxc
一般 ACM 或者笔试题的时间限制是\(1\)秒或\(2\)秒。
在这种情况下,C++ 代码中的操作次数控制在\(10^7 \sim 10^8\)为最佳。
下面给出在不同数据范围下,代码的时间复杂度和算法该如何选择:
1.\(n \leqslant 30\):指数级别、DFS+剪枝、状态压缩DP;
2.\(n \leqslant 100 \Rightarrow O(n^3)\):Floyd、DP、高斯消元;
3.\(n \leqslant 1000 \Rightarrow O(n^2),\; O(n^2logn)\):DP、二分、朴素版Dijkstra、朴素版Prim、Bellman-Ford;
4.\(n \leqslant 10000 \Rightarrow O(n\sqrt n)\):块状链表、分块、莫队;
5.\(n \leqslant 100000 \Rightarrow O(nlogn)\):各种sort、线段树、树状数组、set/map、heap、拓扑排序、Dijkstra+heap、Prim+heap、SPFA、求凸包、求半平面交、二分、CDQ分治、整体二分;
6.\(n \leqslant 1000000 \Rightarrow O(n),\;\)以及常数较小的\(O(nlogn)\)算法:单调队列、hash、双指针扫描、并查集、KMP、AC自动机;常数较小的\(O(nlogn)\)的做法:sort、树状数组、heap、Dijkstra、SPFA;
7.\(n \leqslant 10000000 \Rightarrow O(n)\):双指针扫描,KMP、AC自动机、线性筛素数;
8.\(n \leqslant 10^9 \Rightarrow O(\sqrt n)\):判断质数;
9.\(n \leqslant 10^{18} \Rightarrow O(logn)\):最大公约数,快速幂;
10.\(n \leqslant 10^{1000} \Rightarrow O((logn)^2)\):高精度加减乘除;
11.\(n \leqslant 10^{100000} \Rightarrow O(logk \times loglogk)\),\(k\)表示位数:高精度加减、FFT/NTT;
注:这里的\(log\)指的是以\(2\)为底的对数;
递归
int f(int n){
f(n-1);
}
- 递归即自己调用自己
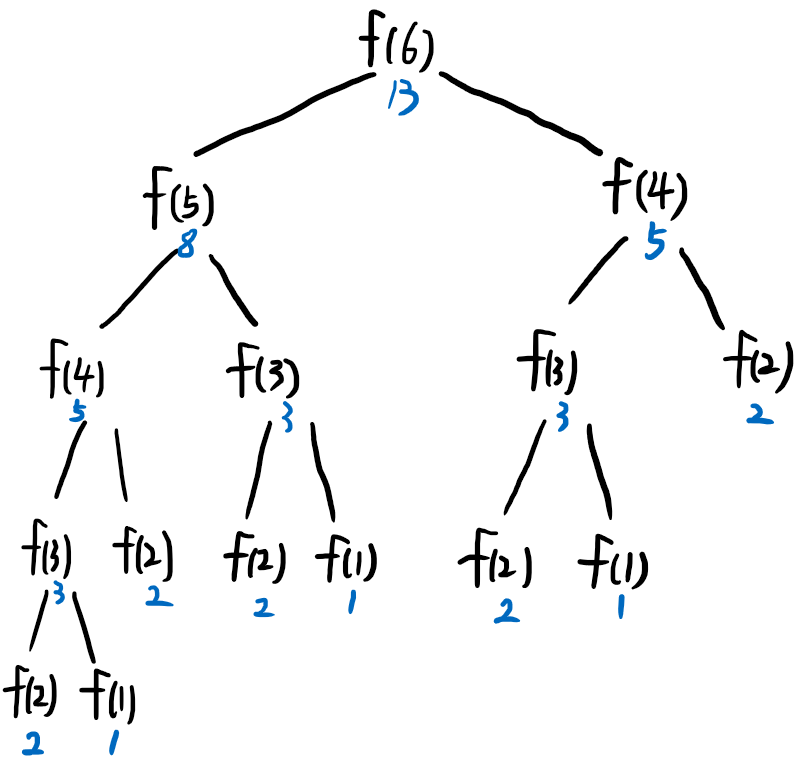
例:斐波那契数列
设\(f=\{1,2,3,5,8,cdots\}\)
\(n=1 \quad f_1=1\);\(n=2 \quad f_2=2\);
$f_n=f_{n-1}+f_{n-2} \quad n \geqslant 3 $
int f(int n){
if(n==1) return 1;
if(n==2) return 2;
return f(n-1)+f(n-2);
}
递归\(\Rightarrow\)递归搜索树
92. 递归实现指数型枚举
从 \(1\sim n\) 这 \(n\) 个整数中随机选取任意多个,输出所有可能的选择方案。
输入格式
输入一个整数 \(n\)。
输出格式
每行输出一种方案。
同一行内的数必须升序排列,相邻两个数用恰好 \(1\) 个空格隔开。
对于没有选任何数的方案,输出空行。
本题有自定义校验器(SPJ),各行(不同方案)之间的顺序任意。
数据范围
\(1\leqslant n \leqslant 15\)
输入样例
3
输出样例
3
2
2 3
1
1 3
1 2
1 2 3
难度: 简单
时/空限制: 5s / 256MB
来源: 《算法竞赛进阶指南》
算法标签:递归
思路
-
数据范围为\(1\leqslant n \leqslant 15\),所以可以用时间复杂度为\(O(2^n)\)的算法来做;
-
对于\(1\sim n\)这\(n\)个数,每个数有 选/不选 两种情况,所以总共的方案数即为\(2^n\),故总的时间复杂度为\(O(n 2^n)\);
-
递归(即DFS),最重要的是顺序,即找一个顺序,可以把所有方案不重不漏地找出来;
-
从\(1 \sim n\),依此考虑每个数 选/不选;
例:\(n=3\)时的递归搜索树
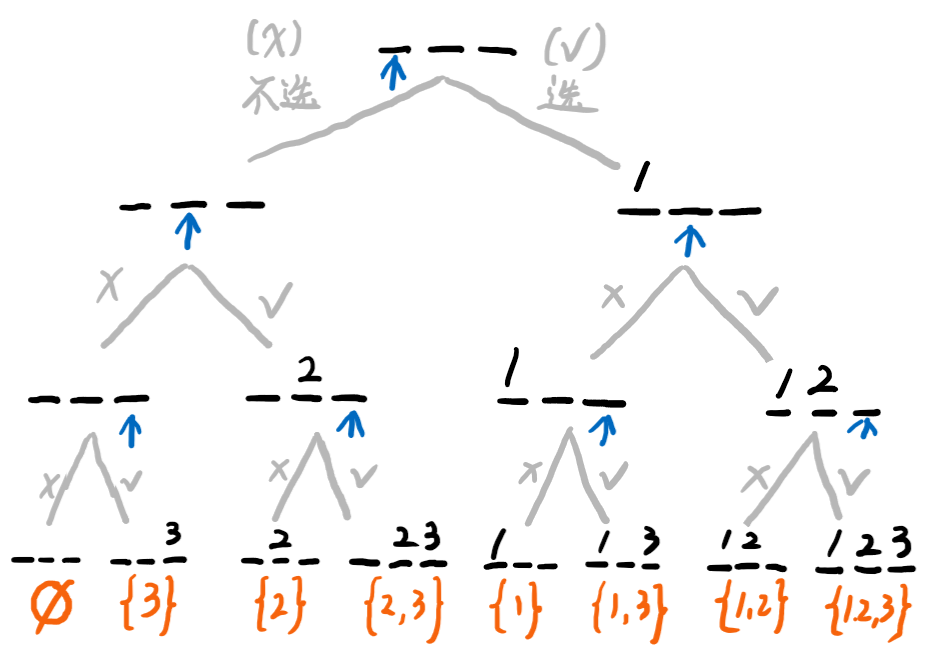
- 状态(即每个数 选/不选)可以开一个长度为\(n\)的数组来记录;
代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=16;
int n;
int st[N];//状态,记录每个位置当前的状态:0表示还没考虑,1表示选它,2表示不选它
void dfs(int u){//u代表当前枚举到第u位
if(u>n){
for(int i=1;i<=n;++i)
if(st[i]==1)
printf("%d ",i);
printf("\n");
return;
}
st[u]=2;
dfs(u+1); //第一个分支:不选
st[u]=0; //恢复现场
st[u]=1;
dfs(u+1); //第二个分支:选
st[u]=0; //恢复现场
}
int main(){
cin>>n;
dfs(1);
return 0;
}
/*
运行时间: 32 ms
运行空间: 856 KB
*/
如果要将方案记录下来
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
const int N=16;
int n;
int st[N];
vector<vector<int>> ways;
//ways代表方案
void dfs(int u){
if(u>n){
vector<int>way;
for(int i=1;i<=n;++i) //记录方案
if(st[i]==1)
way.push_back(i);
ways.push_back(way);
return;
}
st[u]=2;
dfs(u+1);
st[u]=0;
st[u]=1;
dfs(u+1);
st[u]=0;
}
int main(){
cin>>n;
dfs(1);
for(int i=0;i<ways.size();++i){
for(int j=0;j<ways[i].size();++j) printf("%d ",ways[i][j]);
puts("");
}
return 0;
}
/*
运行时间: 89 ms
运行空间: 3084 KB
*/
94. 递归实现排列型枚举
把 \(1\sim n\) 这 \(n\) 个整数排成一行后随机打乱顺序,输出所有可能的次序。
输入格式
一个整数 \(n\)。
输出格式
按照从小到大的顺序输出所有方案,每行 \(1\)个。
首先,同一行相邻两个数用一个空格隔开。
其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面。
数据范围
\(1 \leqslant n \leqslant 9\)
输入样例
3
输出样例
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
难度: 简单
时/空限制: 5s / 256MB
来源: 《算法竞赛进阶指南》
算法标签:递归
思路
- 数据范围为\(1 \leqslant n \leqslant 9\),\(9!=326880\),因此时间复杂度大约为\(O(n \times n!) \Rightarrow DFS\);
字典序:
\(A:a_1,a_2,\cdots,a_n\)
\(B:b_1,b_2,\cdots,b_m\)
\(a_i<b_i\) 或 \(a_i\)不存在但\(b_i\)存在 \(\quad\Rightarrow A<B\)
\(a_i>b_i\) 或 \(b_i\)不存在但\(a_i\)存在 \(\quad\Rightarrow A>B\)
\(n=m\)并且\(a_n=b_m \quad\Rightarrow A=B\)
-
全排列问题一般有两种枚举方式:
1.依此枚举每个数放哪个位置;
2.依此枚举每个位置放哪个数;
对2.的例:\(n=3\)时的递归搜索树
上图保证了(相对意义上的)左子树的方案 字典序一定小于 右子树的方案;
- 开一个长度为\(n\)的数组来记录状态;
代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=10;
int n;
int state[N];// 0 表示还没放数,1~n表示放了哪个数
bool used[N];//true表示用过,false表示还未用过
void dfs(int u){
if(u>n){//边界
for(int i=1;i<=n;++i) printf("%d ",state[i]); //打印方案
puts("");
return;
}
//依次枚举每个分支,即当前位置可以填哪些数
for(int i=1;i<=n;++i)
if(!used[i]){
state[u]=i;
used[i]=true;
dfs(u+1);
//恢复现场
state[u]=0;
used[i]=false;
}
}
int main(){
scanf("%d",&n);
dfs(1);
return 0;
}
/*
运行时间: 373 ms
运行空间: 7000 KB
*/
分析时间复杂度
- 需要递归\(n\)层;
- 第一层时间复杂度为\(O(n)\);(一个
for循环) - 第二层时间复杂度为\(O(n\times n)\);(由第一层衍生出\(n\)个分支,每个分支一个
for循环) - 第三层时间复杂度为\(O(n \times n-1 \times n)\);(由第二层衍生出\(n-1\)个分支)
- \(\cdots\)
- 倒数第二层时间复杂度为\(O(n! \times n)\);
- 最后一层时间复杂度为\(O(n! \times n)\);(最后一层有\(n!\)个结点,且需要输出方案)
总的时间复杂度为\(O[n(1+n+n(n-1)+n(n-1)(n-2)+ \cdots + n!)]\)
相当于\(P_n^0+P_n^1+P_n^2+\cdots +P_n^n \geqslant n!\)
原式相当于:
对其进行放缩:
故整个时间复杂度小于等于\(O(n \times n!)\)
作业
-
AcWing 93.递归实现组合型枚举
-
AcWing 1209.带分数

