2021年蓝桥杯第一次训练赛

A

• TAG：签到题

题面及代码见校内 第一届ACM校赛——热身赛 A题

---

B

More Info中有详细的提示，即注意不要读入行末的换行符，在此不作过多解释。

• TAG：文件读入相关；签到题

PZ.cpp

#include<cstring>
#include<iostream>
#include<string>
using namespace std;
int T;
string s;
int main(){
    scanf("%d\n",&T);
    while(T--){
        getline(cin,s);
        cout<<s<<endl;
    }
    return 0;
}

---

C

• PZ's solution：

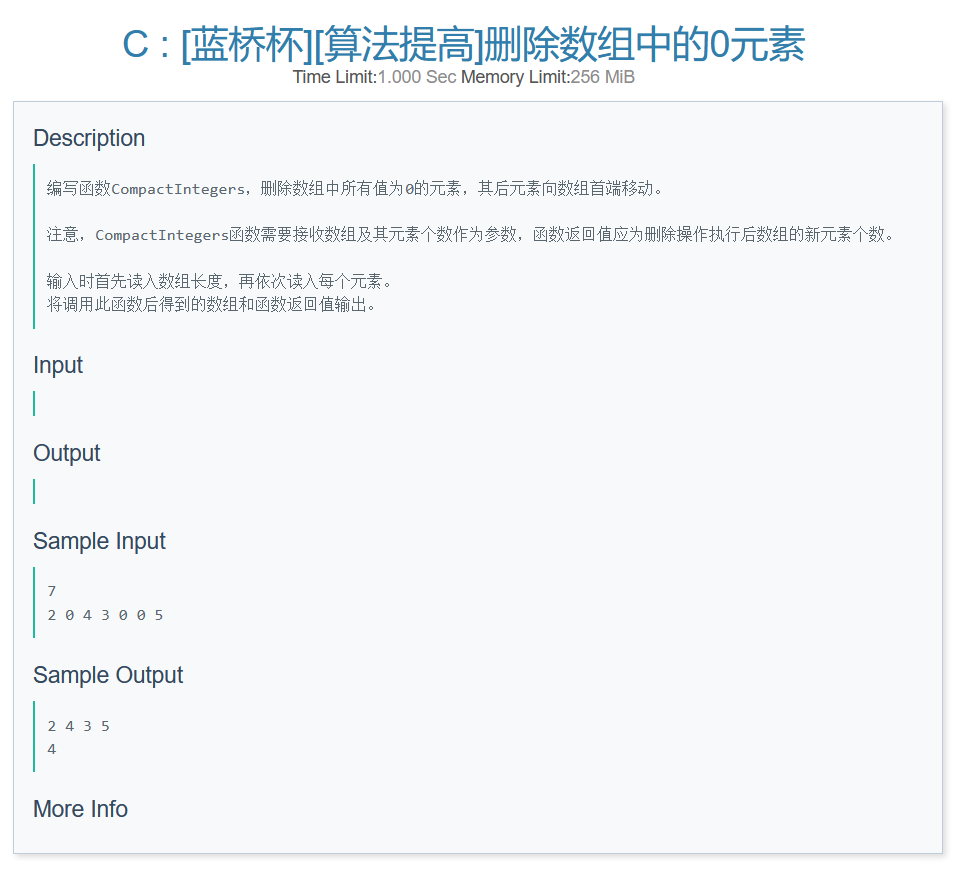
本题题面坚持要求编写这么一个函数，说实话，我嫌麻烦，那么按照题意即可。

注意输入的元素值均为0的情况即可。

• TAG：模拟；签到题

PZ.cpp

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int a[10000005];
int CompactIntegers(int s[],int n){
	int i=1,tmp=0;
	for(int i=1;i<=n;++i) if(s[i]!=0) s[++tmp]=s[i];
	for(int i=1;i<=tmp;++i) printf("%d%c",s[i],(i==tmp ? '\n' : ' '));
	return tmp;
}
int main(){
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;++i) scanf("%d",&a[i]);
	printf("%d",CompactIntegers(a,n));
	return 0;
}

---

D

• PZ's solution：

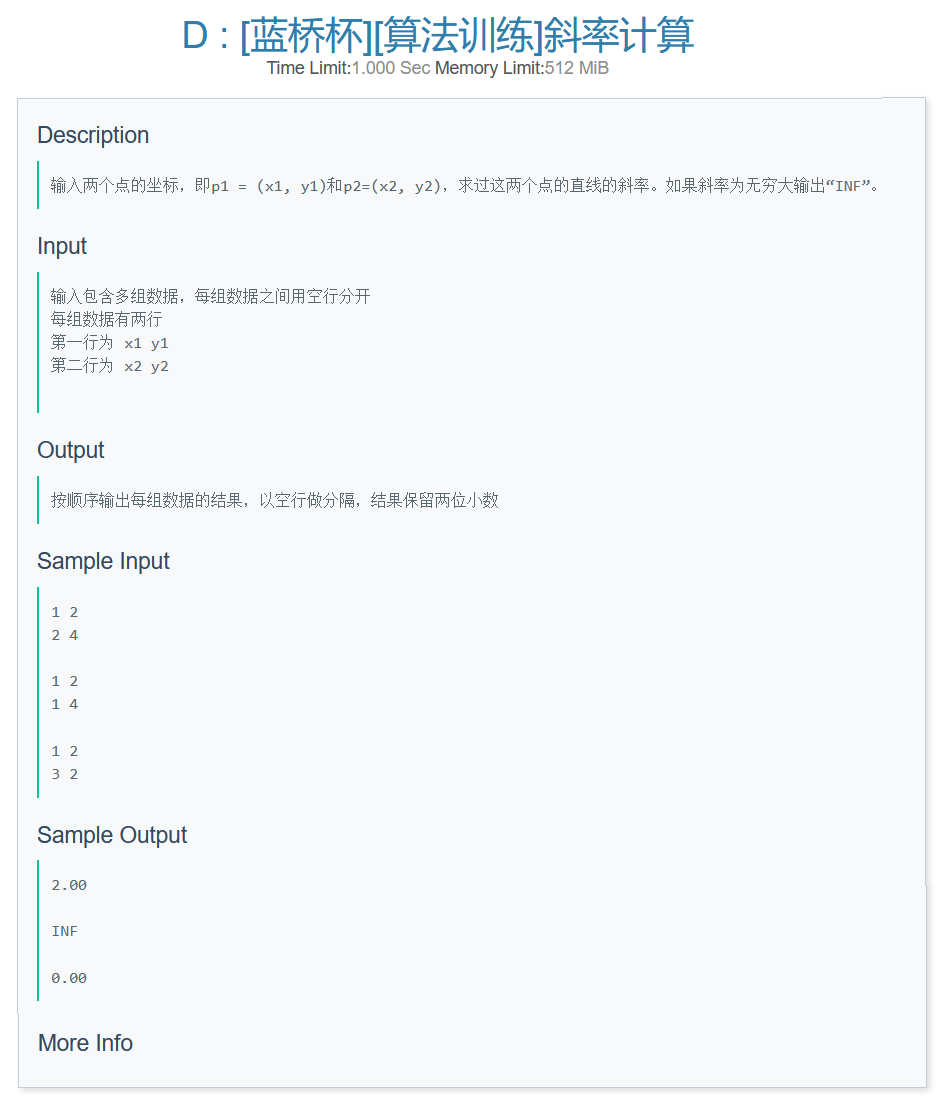
1.对于平面直角坐标系下的两点\((x_1,y_1),(x_2,y_2)\)所构成的直线，若其斜率存在，斜率计算公式为

\[\frac{y_1-y_2}{x_1-x_2} \]

2.当斜率不存在（斜率趋近\(\infty\)）时，当且仅当\(x_1-x_2=0\)；

3.由于C++允许double类型出现 \(-0.0\) 的运算结果，所以对斜率为\(0\)，即\(y_1-y_2=0\)的情况进行特判输出；

• TAG：数学；签到题

PZ.cpp

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
double x_1,x_2,y_1,y_2;
int main(){
	while(scanf("%lf %lf %lf %lf",&x_1,&y_1,&x_2,&y_2)!=EOF){
		if(x_1-x_2==0) printf("INF\n\n");
		else if(y_1-y_2==0) printf("0.00\n");
		else printf("%.2lf\n\n",(y_1-y_2)/(x_1-x_2));
	}
	return 0;
}

---

E

• TAG：模拟；签到题

PZ.cpp

    #include<iostream>
    #include<cstdio>
    #include<cstring>
    #include<algorithm>
    #include<cmath>
    using namespace std;
    int n,ans;
    int main(){
    	scanf("%d",&n);
    	while(n!=1){
    		++ans;
    		if(n%2==0) n=n/2;
    		else n=(3*n+1)/2;
    	}
    	printf("%d",ans);
    	return 0;
    }

---

F

• PZ's solution：

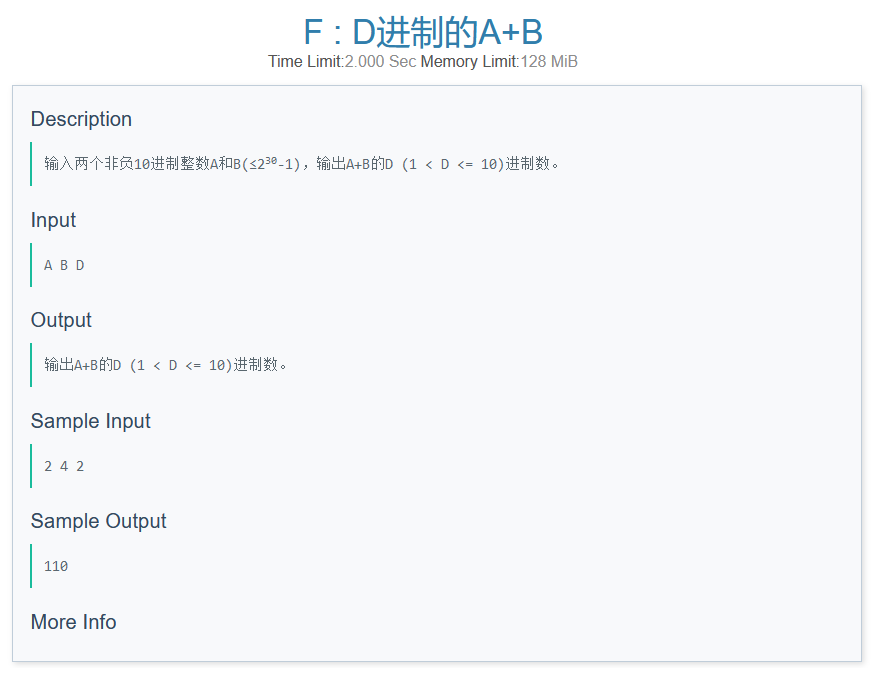
运用短除法，倒序输出余数即可，例如：

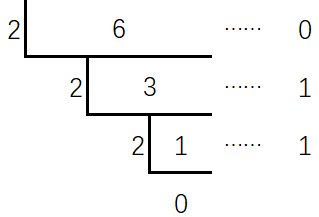
即\(6_{(10)}=110_{(2)}\)

• TAG：数学；签到题

PZ.cpp

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int a,b,d,res,ans[1000005];
int main(){
	scanf("%d %d %d",&a,&b,&d);
	res=a+b;
	while(res!=0){
		ans[++ans[0]]=res%d;
		res/=d;
	}
	for(int i=ans[0];i>=1;--i) printf("%d",ans[i]);
	return 0;
}

---

G

• 快速幂模板，注意p取0或1的情况即可；
• TAG：快速幂；数学

PZ.cpp

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
#define int long long
long long a,b,p;
long long qpow(long long x,long long k){
	if(k==0) return 1%p;
	long long res=x; --k;
	while(k){
		if(k&1) res=res*x%p;
		x=x*x%p;
		k>>=1;
	}
	return res;
}
signed main(){
	scanf("%lld %lld %lld",&a,&b,&p);
	printf("%lld",qpow(a,b));
	return 0;
}

---

赛后总结

1.本次比赛比较基础，所有集训队队员应该在比赛期间将所有题目尽数AC；

2.对于本次比赛，A~E题比较基础，其中：

B题考察了ACM竞赛中可能出现的读入陷阱；

C题虽然题面看似要求苛刻，但完成方法很多，如果不是基本语句掌握不熟练，不必强求按照累赘的方法完成本题；

D题考察了ACM竞赛中可能出现的输出陷阱（对于集训队队员来说，这是本次比赛不能犯的错误，因为这一陷阱在之前的练习题HDU 3500 Fling出现过）；

3.F题考察了进制转换，对此不熟悉的同学应该加强练习，进制运算是算法竞赛中十分常见的内容，而且也是很多算法的点睛之笔；

4.G题承接自F题，真正考察了一个比较套路的算法：快速幂，快速幂的理解与进制转换密不可分，这里给出题人点个赞(๑•̀ㅂ•́)و✧；

5.总的来说，为了照顾到所有在校学生，本次比赛的难度是有所克制的（看看寒假第一次练习赛就知道，难度的差距是天上地下），而集训队成员要快速准确完成这些题目，并熟稔于心，向蓝桥杯进发！

ps.蓝桥杯的历届真题，我会去更的，我不想当鸽子，咕咕咕~