4.6 Python3 进阶 - 递归函数

>>返回主目录

源码

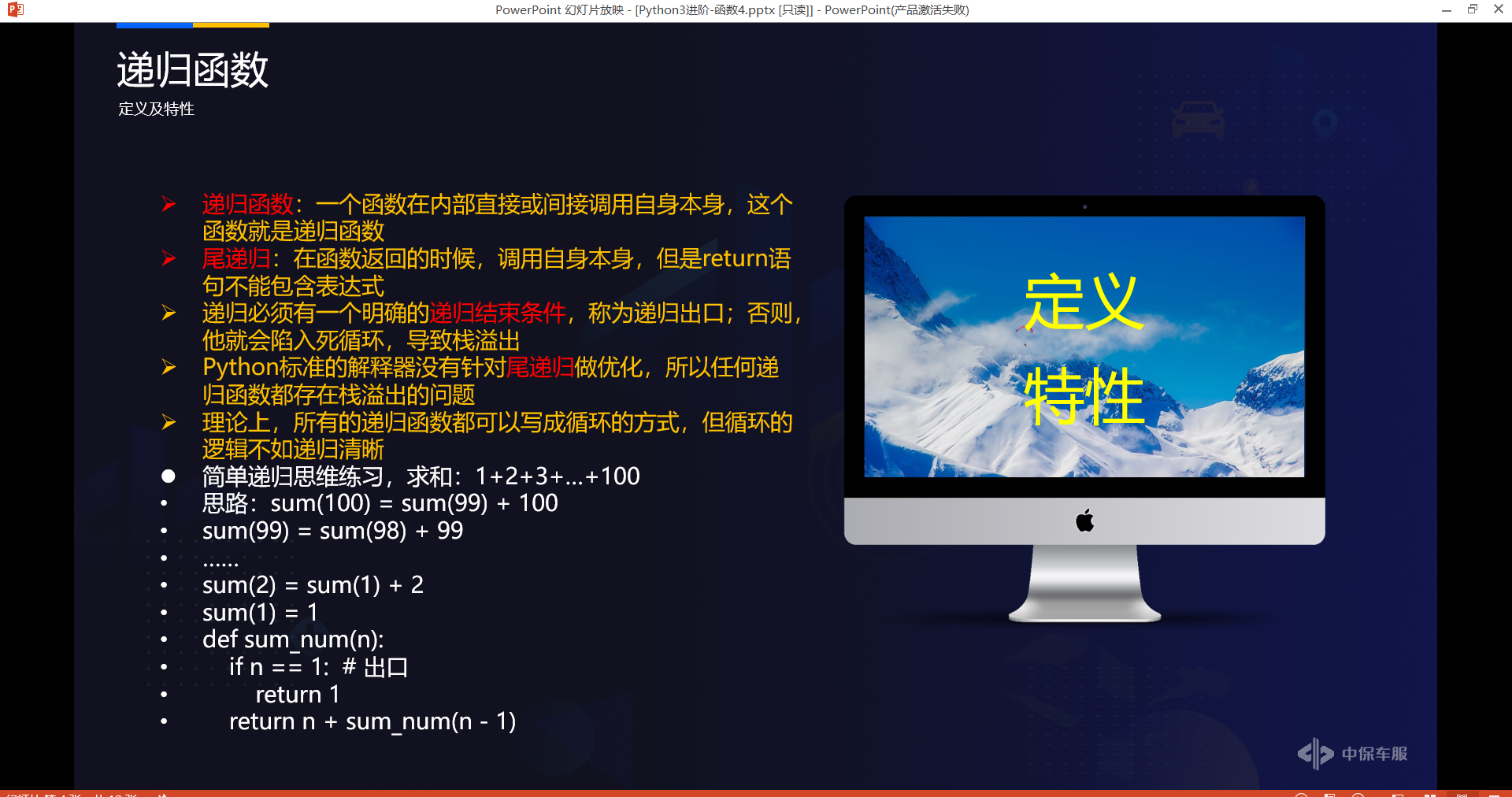
# 定义及特性
# 简单递归思维练习，求和：1+2+3+…+100
# 思路：sum(100) = sum(99) + 100
# sum(99) = sum(98) + 99
# ……
# sum(2) = sum(1) + 2
# sum(1) = 1


def sum_num(n):
    if n == 1:  # 出口
        return 1
    return n + sum_num(n - 1)


print(sum_num(5))

源码

# 优缺点
# 巩固递归思维，求：5!
# 思路：5! = 1 * 2 * 3 * 4 * 5 = 5 * 4! = 5 * (4 * 3!)
# 利用数学归纳法，推导出递归表达式：n! = n * (n - 1)!
# 再使用函数实现：
def factorial(n):
    if n == 1:
        return 1  # 递归结束
    return n * factorial(n - 1)  # 问题规模减1，递归调用


print(factorial(5))


# 巩固递归执行过程：
def factorial_exe(n):
    print(n, '去的过程')
    if n > 0:
        factorial_exe(n-1)
        # return factorial_exe(n-1)
    print(n, '回的过程')
    return n


factorial_exe(5)

源码

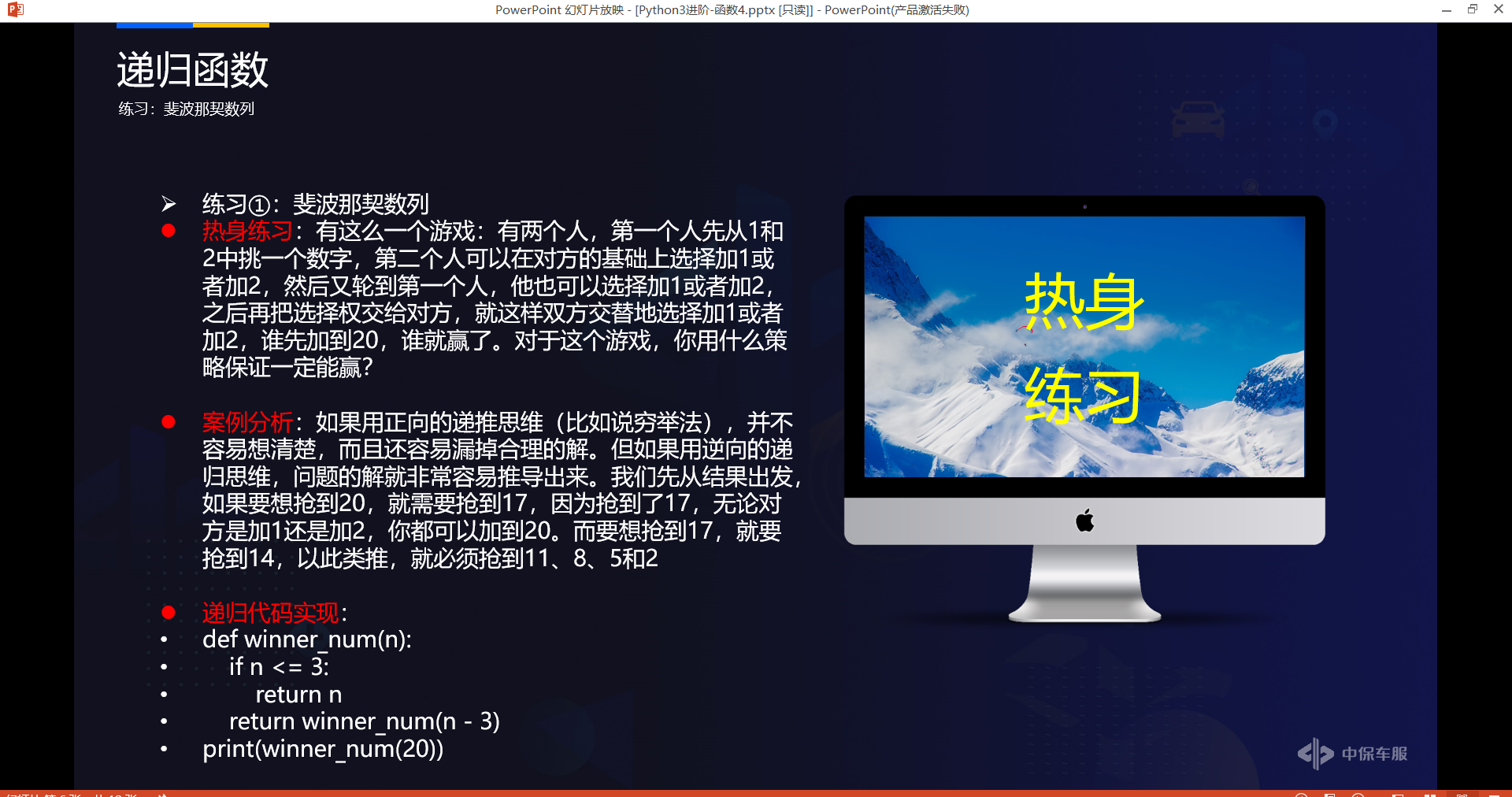
# 练习①
# 递归代码实现：
def winner_num(n):  # n为最终要加到的数
    if n <= 3:
        return n
    return winner_num(n - 3)


print('想要赢得比赛，必须要抢到的数是：', winner_num(4))

源码

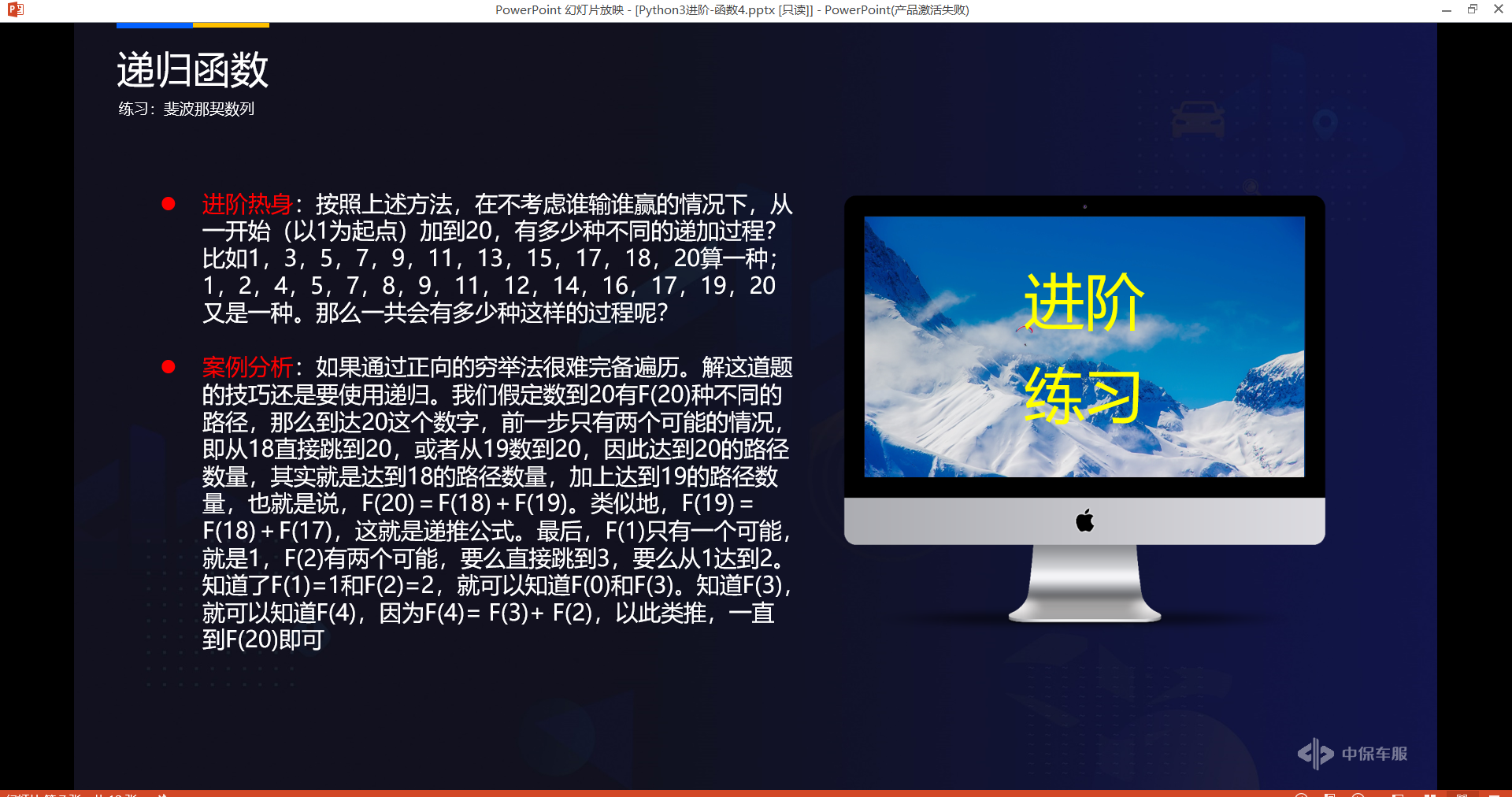
# 斐波那契数列
# 代码实现：
def fibon(n):  # 参数是表示第n个斐波那契数，函数整体表示获取斐波那契数列中第n个数字的值
    if n == 0:
        return 0  # fibon(0) = 0
    elif n == 1 or n == 2:
        return 1  # fibon(1) = fibon(2) = 1
    return fibon(n-1) + fibon(n-2)  # fibon(n) = fibon(n-1) + fibon(n-2) (n >= 2)


num = 5
print(f'此斐波那契数列第{num}个数是:', fibon(num))


# 列出这个斐波那契额数列
fibon_list = []
for i in range(num + 1):
    fibon_list.append(fibon(i))
print(f'这个斐波那契额数列是：{fibon_list}')

源码

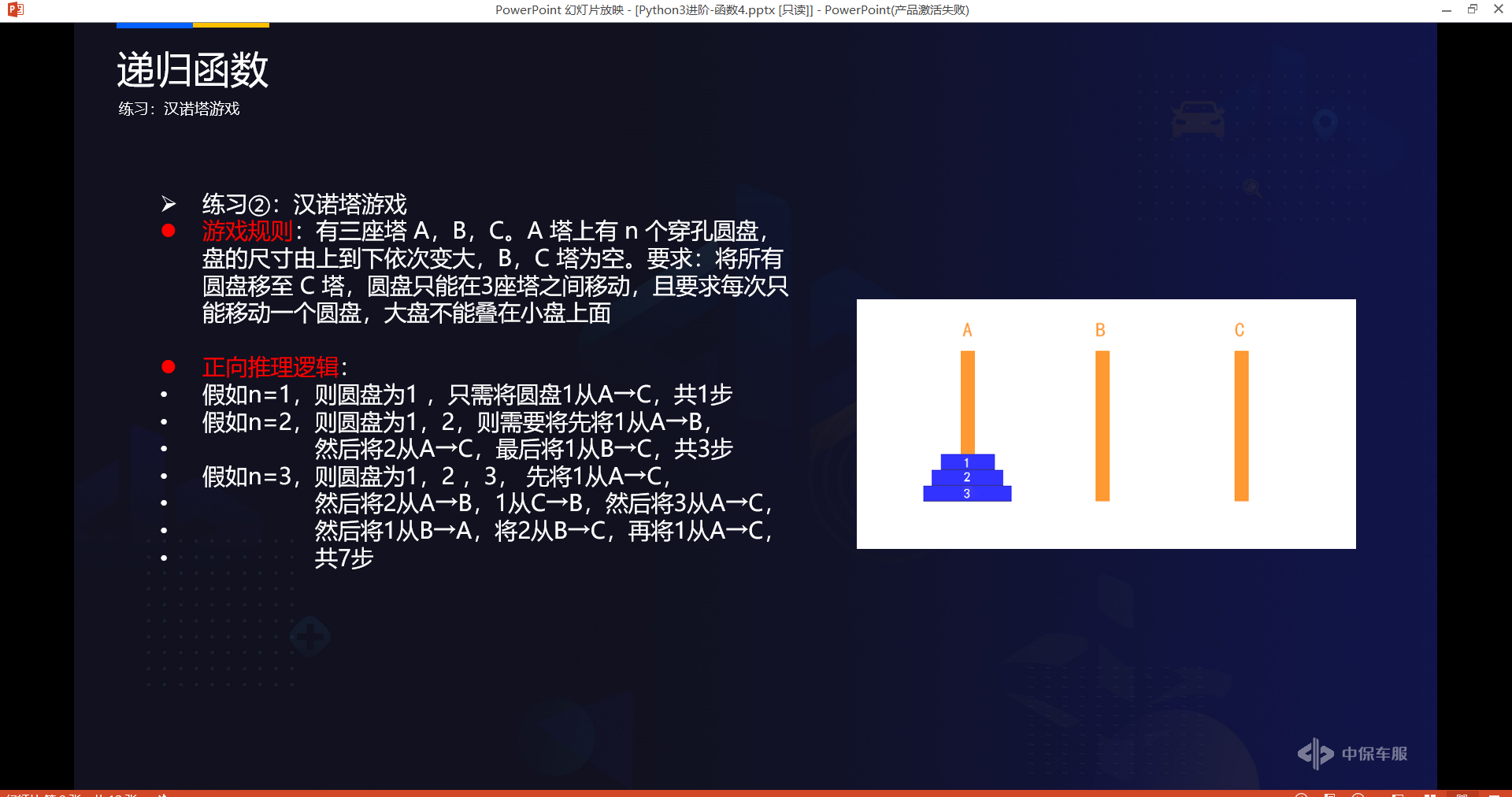
# 练习②汉诺塔游戏
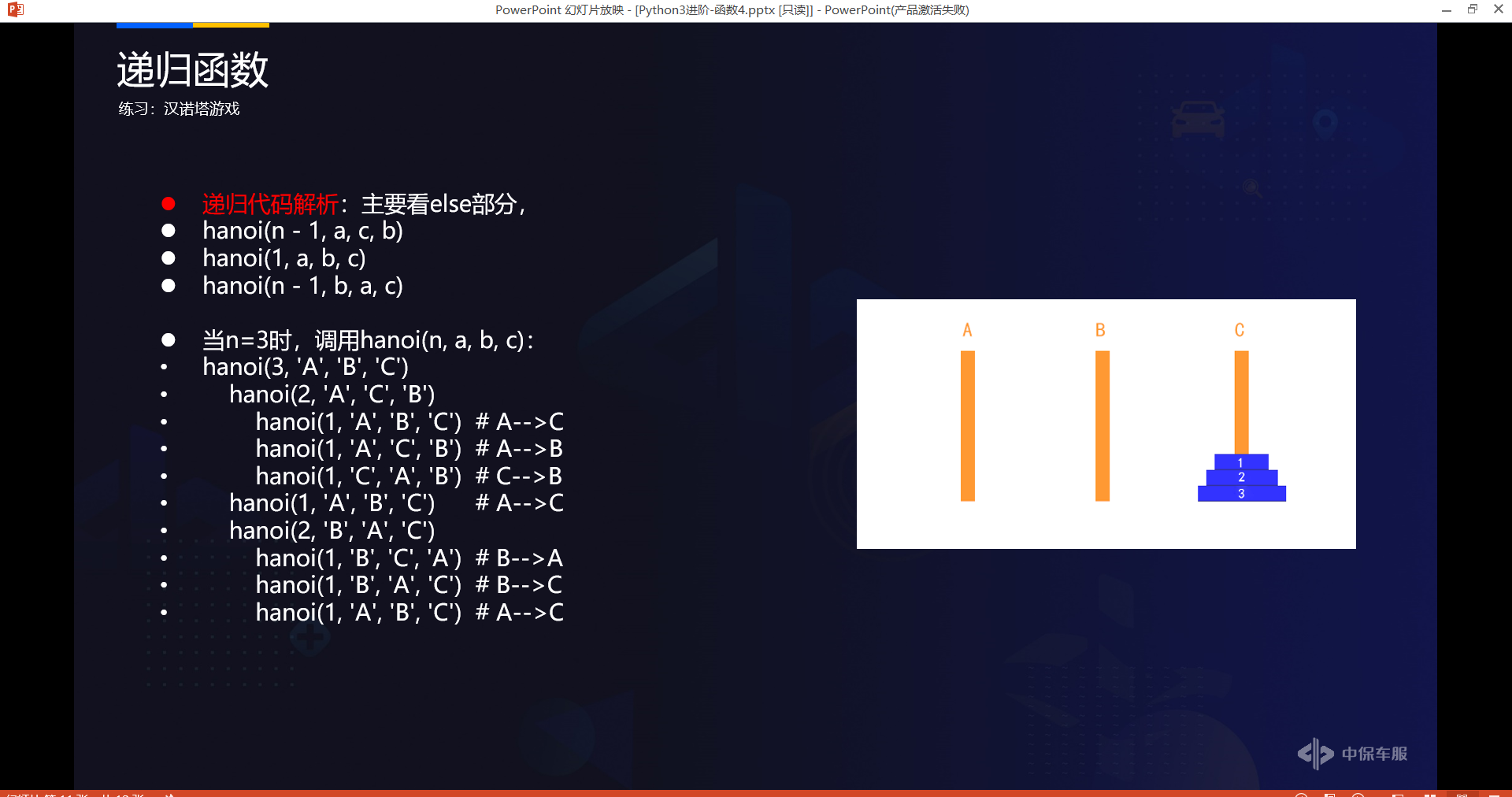
# 递归代码实现：区分n=1和n>1的情况，具体实现如下：
i = 1


def hanoi_1(n, a, b, c):
    global i
    if n == 1:
        print(f'第{i}步：', a, '-->', c)
        i += 1
    else:
        hanoi_1(n - 1, a, c, b)
        hanoi_1(1, a, b, c)
        hanoi_1(n - 1, b, a, c)


num = 3  # 圆盘个数
print('把', num, '个盘子全部移到C柱子的顺序为：')
hanoi_1(num, 'A', 'B', 'C')


# 完善解法二
m = 1


def move(n, mfrom, mto):
    global m
    print("第%d步:将%d号盘子从%s -> %s" % (m, n, mfrom, mto))
    m += 1


def hanoi_2(n, a, b, c):
    if n == 1:
        move(1, a, b)
    else:
        hanoi_2(n - 1, a, c, b)
        move(n, a, c)
        hanoi_2(n - 1, b, a, c)


print("移动步骤如下：")
hanoi_2(3, 'A', 'B', 'C')

>>返回主目录