Deep Learning 学习笔记（6）：神经网络( Neural Network )

神经元：

在神经网络的模型中，神经元可以表示如下

神经元的左边是其输入，包括变量x1、x2、x3与常数项1，

右边是神经元的输出

 

神经元的输出函数被称为激活函数（activation function），输出值被称为激活值（activation value）。

激活函数有很多种，其中最简单的莫过于sigmoid函数。

除非特别声明，否则博客里提及的激活函数均为sigmoid

 

神经网络：

多个神经元首尾相连连接成神经网络（Neural Network），可以表示如下：

 

尽管生物体中神经云之间的连接会更加复杂，

在常用的模型中，神经元的连接要遵循一定规则，

简单地来说就是要分层：上一层神经元的输出作为下一层的输入，

两层之间单向传递，没有反馈

同层之间的神经元没有交流。

 

下面我们来描述一下这个模型 :

神经网络 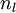\textstyle {n}_l 来表示网络的层数，

其中最左边的叫做出入层，最右边的称为输出层，中间的层被称为隐藏层

隐藏层的借点成为隐藏节点。隐藏层的数量为网络的“深度”

 

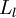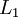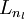我们将第 \textstyle l 层记为 \textstyle L_l ，于是 \textstyle L_1 是输入层，输出层是 \textstyle L_{n_l} 。

 

本例神经网络有参数 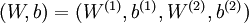\textstyle (W,b) = (W^{(1)}, b^{(1)}, W^{(2)}, b^{(2)}) ，

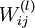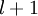其中 ， \textstyle W^{(l)}_{ij} （下面的式子中用到）是第 \textstyle l 层第 \textstyle j 单元与第 \textstyle l+1 层第 \textstyle i 单元之间的联接参数（权重，注意标号顺序）， 

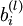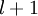\textstyle b^{(l)}_i 是第 \textstyle l+1 层第 \textstyle i 单元的偏置项。

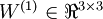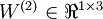因此在本例中， \textstyle W^{(1)} \in \Re^{3\times 3} ， \textstyle W^{(2)} \in \Re^{1\times 3} 。

注意，即偏置单元没有输入

 

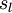 \textstyle s_l 表示第 \textstyle l 层的节点数，偏置单元不计在内

神经网络的计算：

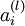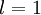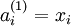
用 \textstyle a^{(l)}_i 表示第 \textstyle l 层第 \textstyle i 单元的激活值（输出值），当 \textstyle l=1 时， \textstyle a^{(1)}_i = x_i

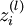\textstyle z^{(l)}_i 表示第 \textstyle l 层第 \textstyle i 单元输入加权和（包括偏置单元）

于是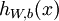，\textstyle h_{W,b}(x)  可以按如下方法计算

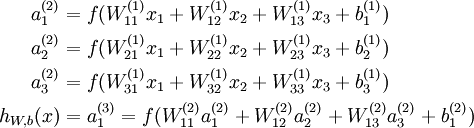
\begin{align} a_1^{(2)} &= f(W_{11}^{(1)}x_1 + W_{12}^{(1)} x_2 + W_{13}^{(1)} x_3 + b_1^{(1)}) \\ a_2^{(2)} &= f(W_{21}^{(1)}x_1 + W_{22}^{(1)} x_2 + W_{23}^{(1)} x_3 + b_2^{(1)}) \\ a_3^{(2)} &= f(W_{31}^{(1)}x_1 + W_{32}^{(1)} x_2 + W_{33}^{(1)} x_3 + b_3^{(1)}) \\ h_{W,b}(x) &= a_1^{(3)} = f(W_{11}^{(2)}a_1^{(2)} + W_{12}^{(2)} a_2^{(2)} + W_{13}^{(2)} a_3^{(2)} + b_1^{(2)}) \end{align}

 

 

计算过程可以用向量运算简化

这种由输入求输出，从左向右计算的算法，叫做前向传播算法

于是乎这种神经网络也叫做前馈神经网络

 

（完)

 

 

 

 

 

 

 

 

 

 

posted @ 2013-09-09 19:46  Pony_s  阅读(955)  评论(0)  编辑  收藏  举报