模拟费用流的一些小思考
感觉模拟费用流这个东西几乎可以和反悔贪心画上等号了(可能是我菜,所以理解有问题,欢迎开 d ),但是具体实施下来还是有许多的细节的。
如果是两两匹配的问题,实际上我们只需要将自己的反向情况塞到另一方的堆里,通过这种方式来实现退流的操作。如果是不需要满足最大流的费用流,我们是可以直接做的,但是这个方法在我们需要满足最大流的情况下求最小费用时就不那么有效了,因为我们不能保证流量是最大的。
具体的,我们以一道例题为例。
例子
我们考虑到这题就需要满足一个最大流的条件,所以我们要列出所有可能的退流情况。
首先,我们必然是考虑从左到右依次加入的,那么我们实际上是默认该点只能向自己的左边连边,所以我们要设置两种反悔,分别对应两种点向右边连边的情况。同时,还存在一般的反悔,即都在右边连边的情况下,反悔前者,使用后者。
此时我们再来考虑这几种反悔的流量,由于此题中第一种点的数量较少,所以最大流必然就是第一个点的数量。考虑我们让所有第一个点的有关流量都必须流,无论大小,但是对于第二种点的流,我们就需要贪心只流小于 \(0\) 的,这样方可使答案最小。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=1e5+5;
const long long INF=1e13;
int n,m;
struct People{int x;}a[N];
struct Restaurant{int x,c,w;}b[M];
struct Object{long long w;mutable int cnt;};
bool operator < (Object a,Object b){return a.w>b.w;}
priority_queue<Object> q1,q2;
long long cnt=0,res=0;
int main(){
cin>>n>>m;
for(int i=1;i<=n;++i) scanf("%d",&a[i].x);
for(int i=1;i<=m;++i) scanf("%d%d%d",&b[i].x,&b[i].w,&b[i].c);
for(int i=1;i<=m;++i) cnt+=b[i].c;
if(cnt<n) return printf("-1\n"),0;
q2.push((Object{INF,n}));
for(int i=1,j=1;i<=n||j<=m;){
if(i<=n&&(j>m||a[i].x<b[j].x)){
long long tmp=q2.top().w+a[i].x;
if(!(--q2.top().cnt)) q2.pop();
res+=tmp,q1.push((Object){-tmp-a[i].x,1});
i++;
}
else{
int CNT=0;
while(!q1.empty()&&CNT<b[j].c){
long long tmp=q1.top().w+b[j].x+b[j].w;if(tmp>=0) break;
int cnt=min(q1.top().cnt,b[j].c-CNT);
if(!(q1.top().cnt-=cnt)) q1.pop();
CNT+=cnt,res+=tmp*cnt,q2.push((Object){-tmp-b[j].x+b[j].w,cnt});
}
if(CNT) q1.push((Object){-b[j].x-b[j].w,CNT});
if(b[j].c-CNT) q2.push((Object){-b[j].x+b[j].w,b[j].c-CNT});
j++;
}
}
return printf("%lld\n",res),0;
}
/*
我们考虑可以建出一个比较简单的费用流模型,具体的,考虑将所有点排序,相邻两点间连以距离
为费用的边,然后每个餐厅再向汇点连对应流量和费用的边。
我们需要考虑模拟这个费用流。具体的,我们考虑反悔贪心,维护两个堆表示目前价值最小的送餐
员和餐厅,然后考虑选择一对之后,将其反面也丢入另一侧的堆中。
*/
总结
模拟费用流说到底还是大模拟,所以我们需要结合题目的具体费用流模型来设计符合要求的反悔贪心策略,一般考虑找到限制最大流的位置,这种流不能轻易退流,其他的即可贪心退流。又或者是存在使得流量始终加一的反悔贪心做法,这也是一种不错的想法。
P5470 [NOI2019] 序列
课后作业。首先考虑建出一个费用流模型。
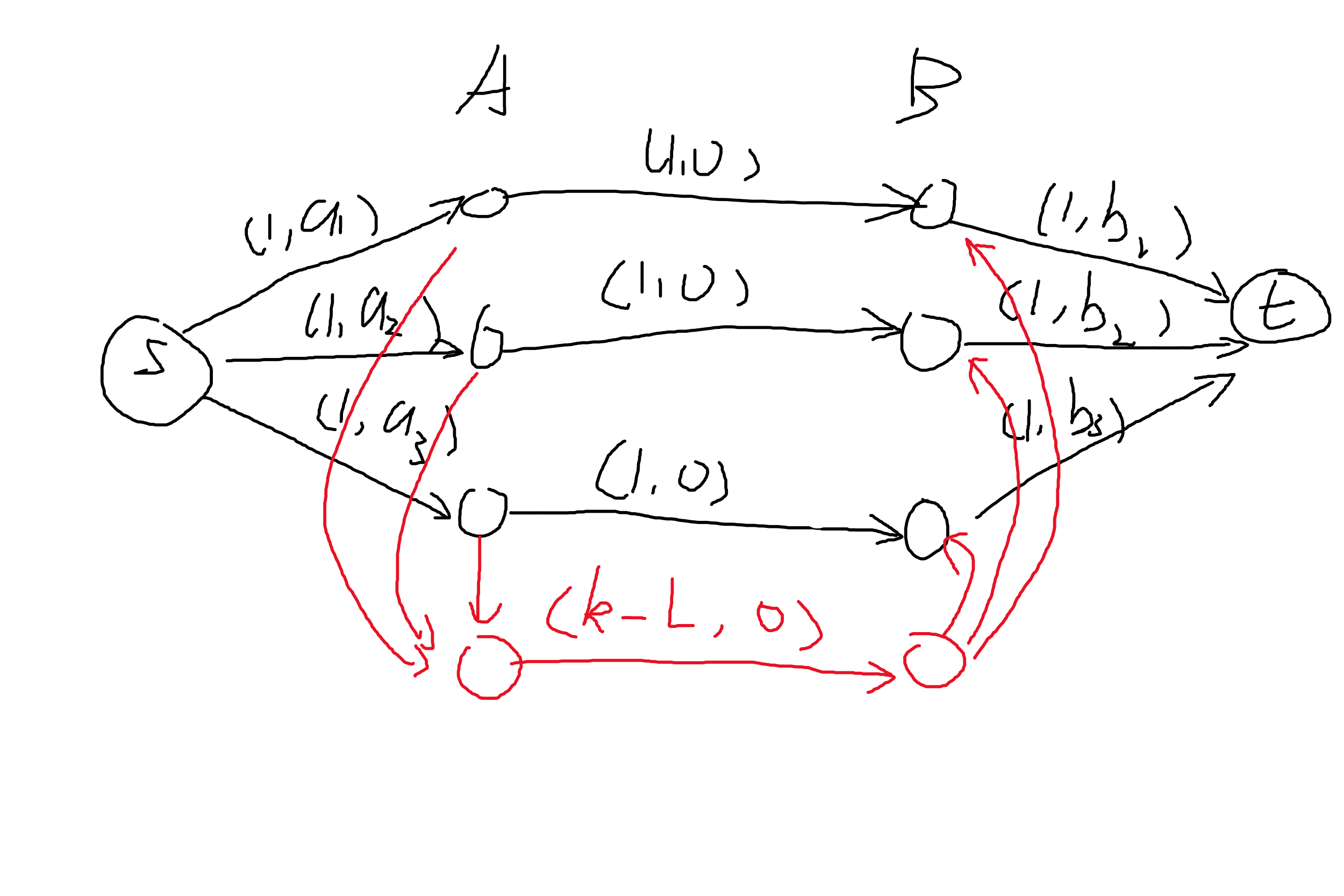
由于我们是两个序列各选 \(k\) 个,我们可以理解为选择 \(k\) 对,这样的话,每对有着相同或者不同两种情况,其中相同对的个数需要大于等于 \(l\) ,意味着不同对的个数需要小于等于 \(k-l\) 。由于上面的模型中,不同对的数只能走最下面的边,于是我们便限制了相同的对数。
跑流量为 \(k\) 的最大费用即可。
我们考虑如何用模拟费用流来处理这个模型。不会,全文完。
如何提高费用流效率?我们有个叫“模拟费用流”的东西。说白了,我对模拟费用流的理解就是,在特殊条件允许下,用贪心来取代 spfa 找最短路,用各种手段(代价取反、分类讨论等等)来模拟退流过程。
那么我们需要通过分析题目性质,通过恰当的贪心策略,得到最优的方案。
策略一:流量限制为 \(k-l\) 的边一定是有就走。
证明:显然,因为除了流量限制之外这个边是没有限制的。
具体实现:我们用两个堆维护当前自由的 \(a_i\) 和 \(b_i\) ,每次取出来最大的,如果两者的标号相同,就不消耗该边的流量,否则消耗一。
策略二:在不退流的情况下,我们考虑最大的一对 \(a_i,b_i\) ,直接选取即可。
策略三:考虑退流,即我们找到一个已经匹配的 \(a_i\) 和还未匹配的 \(b_i\) ,和另一任意 \(a_j\) ,三者加上 \(a_i\) 所匹配的那个一共四个重新连边即可。
策略四:基本同策略三,考虑两者的 \(a,b\) 位置交换。
感觉代码实现方面和上述策略的优先度方面需要仔细揣度,具体的,费用最大的优先选,费用相同的看能否减少特殊边的流量。
但是存在一个奇怪的问题,即我们如果将其作为模拟费用流的过程,我们当前每一步的操作实际上就是找到当前的最长路。为什么还需要考虑这一步对于后面的流量的影响呢?
哦,实际上这也是一个退流,退流的方式通过贪心表达出来就是上述那样,所以我们实际上可以更加形式化地表述这个过程。
我们考虑对于上面那张图的每一种边都维护一个堆,然后结合上述策略执行即可?
应该是这样的,具体的,第一个堆维护 \(S\rightarrow A\) ,第二个堆维护 \(B\rightarrow T\) ,第三个堆维护 \(A\rightarrow B\) ,第四个堆维护 \(S\rightarrow A\rightarrow C\) , 第五个堆维护 \(D\rightarrow B\rightarrow T\) ,第六个堆维护 \(C\rightarrow D\) 。
应该就是这样,代码咕咕咕。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号