P5838 [USACO19DEC]Milk Visits G

发现是一道比较裸的树上莫队，于是就开始刚，然后发现好像是最难的一道题……（本题解用于作者加深算法理解，也欢迎各位的阅读）

题意

给你一棵树，树有点权，询问一条路径上是否有点权为 \(c\) 的点。

题解

我们可以比较明显地发现询问是很像莫队的询问处理的，可以 \(O(1)\) 去扩展 \(l\) 和 \(r\) 。但是这题是树，所以我们需要引入欧拉序的概念。

欧拉序其实很像 \(dfs\) 序，但是会在出栈的时候多记录一次，我们可以利用欧拉序来将树上的路径转化为莫队需要的区间问题。

我们可以先画一张图：

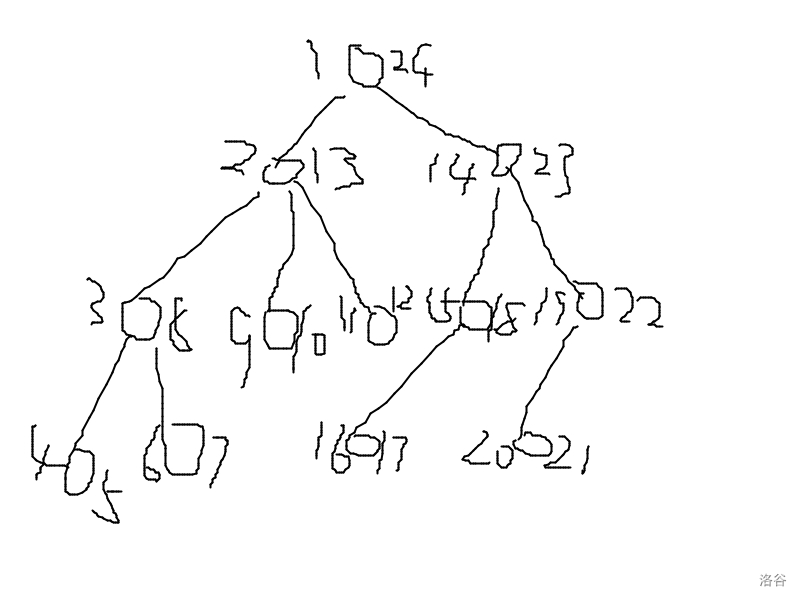
其中位于节点右侧的是入栈时间，位于节点左侧的是出栈时间。

我们不妨以每一个点的入栈时间为编号，欧拉序则为：

\[1~2~3~4~4~6~6~3~9~9~11~11~2~14~15~16~16~15~19~20~20~19~14~1 \]

比如对于 \(9\) ~ \(16\) 这一条路径，我们可以用时间 \(10\) ~ \(16\) 来表示，其中出现两次的点我们不进行计算，并且还需要多加上 \(9\) 和 \(16\) 的 \(lca\)：\(1\) ，这些可以用异或运算和特判来解决。即路径 \(x\) ~ \(y\)：\(lst_x\) ~ \(fir_y\) 。

同时我们可以发现，如果路径上的点是为祖先关系，我们需要特殊处理，可以发现是 \(fir_x\) ~ \(fir_y\) 。

因此我们将所有的路径都转化为区间之后就可以用莫队离线实现了，复杂度 \(O(n\sqrt n)\) 。可是不开 \(O2\) 过不了……

以上。

代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=1e5+5;
int n,m,type[N];
struct Edge{int nxt,to;}e[N<<1];int head[N];
void add(int u,int v,int i){e[i]=Edge{head[u],v},head[u]=i;}
int fir[N],lst[N],dfn[N<<1],cnt_dfn=0;
int dep[N],fa[N][25];
void dfs(int u)
{
	dfn[++cnt_dfn]=u,fir[u]=cnt_dfn;
	for(int i=head[u];i;i=e[i].nxt)
	{
		if(e[i].to==fa[u][0]) continue;
		fa[e[i].to][0]=u;
		dep[e[i].to]=dep[u]+1;
		dfs(e[i].to);
	}
	dfn[++cnt_dfn]=u,lst[u]=cnt_dfn;
}
int lca(int u,int v)
{
	if(dep[u]>dep[v]) swap(u,v);
	for(int i=20;i>=0;--i)
	{
		if(dep[fa[v][i]]>=dep[u])
		v=fa[v][i];
	}
	if(u==v) return u;
	for(int i=20;i>=0;--i)
	{
		if(fa[u][i]!=fa[v][i])
		u=fa[u][i],v=fa[v][i];
	}
	return fa[u][0];
}
struct Query{int l,r,lca,c,id;}q[M];
int bel[N<<1],size;
bool cmp(Query a,Query b)
{
	if(bel[a.l]^bel[b.l]) return bel[a.l]<bel[b.l];
	if(bel[a.l]^1) return a.r<b.r;
	return a.r>b.r;
}
int l=1,r=0,tag[N],cnt[N],ans[M];
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;++i) scanf("%d",&type[i]);
	for(int i=1,u,v;i<n;++i)
	{
		scanf("%d%d",&u,&v);
		add(u,v,i<<1);
		add(v,u,i<<1|1);
	}
	dep[1]=1,dfs(1);
	for(int i=1;i<=20;++i)
	{
		for(int j=1;j<=n;++j)
		fa[j][i]=fa[fa[j][i-1]][i-1];
	}
	size=sqrt(n*2);
	for(int i=1,cnt=0;i<=n*2;i+=size)
	{
		++cnt;
		for(int j=i;j<min(i+size,n*2+1);++j)
		bel[j]=cnt;
	}
	for(int i=1;i<=m;++i)
	{
		scanf("%d%d%d",&q[i].l,&q[i].r,&q[i].c),q[i].id=i;
		if(fir[q[i].l]>fir[q[i].r]) swap(q[i].l,q[i].r);
		q[i].lca=lca(q[i].l,q[i].r);
		if(q[i].lca==q[i].l) q[i].l=fir[q[i].l];
		else q[i].l=lst[q[i].l];
		q[i].r=fir[q[i].r];
	}
	// for(int i=1;i<=n*2;++i)
	// printf("%d ",dfn[i]);
	// printf("\n");
	sort(q+1,q+1+m,cmp);
	// for(int i=1;i<=m;++i)
	// printf("%d %d %d\n",q[i].l,q[i].r,q[i].lca);
	for(int i=1;i<=m;++i)
	{
		while(q[i].r>r)
		{
			tag[dfn[++r]]^=1;
			if(tag[dfn[r]]) cnt[type[dfn[r]]]++;
			else cnt[type[dfn[r]]]--;
		}
		while(q[i].r<r)
		{
			tag[dfn[r]]^=1;
			if(tag[dfn[r]]) cnt[type[dfn[r--]]]++;
			else cnt[type[dfn[r--]]]--;
		}
		while(q[i].l>l)
		{
			tag[dfn[l]]^=1;
			if(tag[dfn[l]]) cnt[type[dfn[l++]]]++;
			else cnt[type[dfn[l++]]]--;
		}
		while(q[i].l<l)
		{
			tag[dfn[--l]]^=1;
			if(tag[dfn[l]]) cnt[type[dfn[l]]]++;
			else cnt[type[dfn[l]]]--;
		}
		// printf("$$$%d %d\n",l,r);
		// for(multiset<int>::iterator i=st.begin();i!=st.end();++i)
		// printf("%d ",*i);
		// printf("\n");
		ans[q[i].id]=(cnt[q[i].c]||type[q[i].lca]==q[i].c);
	}
	for(int i=1;i<=m;++i) printf("%d",ans[i]);
	printf("\n");
	return 0;
}