CF786B Legacy

我表示这是老早以前的 \(XJ\) 练习题，但是我一直在咕咕咕，所以现在才做完。

题目大意

给你三种建图方式：

• 点 \(u\) 向点 \(v\) 连一条边，边权为 \(w\) 。
• 点 \(u\) 向 \([l,r]\) 区间内的点连一条边，边权均为 \(w\)。
• \([l,r]\) 区间内的点向点 \(v\) 连一条边，边权均为 \(w\)。

最后询问你一个点的单源最短路。

题解

我们可以比较轻易的想到，这是一道关于区间操作的题，我们需要一些关于区间操作的数据结构来优化连边，因为直接连边是肯定会炸的。

表示我们可以考虑线段树。因为向一段区间连边在线段树上就可以表示为向 \(log\) 级别个数的节点连边，那么我们只要将这棵线段树的父节点与子节点之间的连边处理好，就可以利用线段树的节点作为点的编号来进行建图。

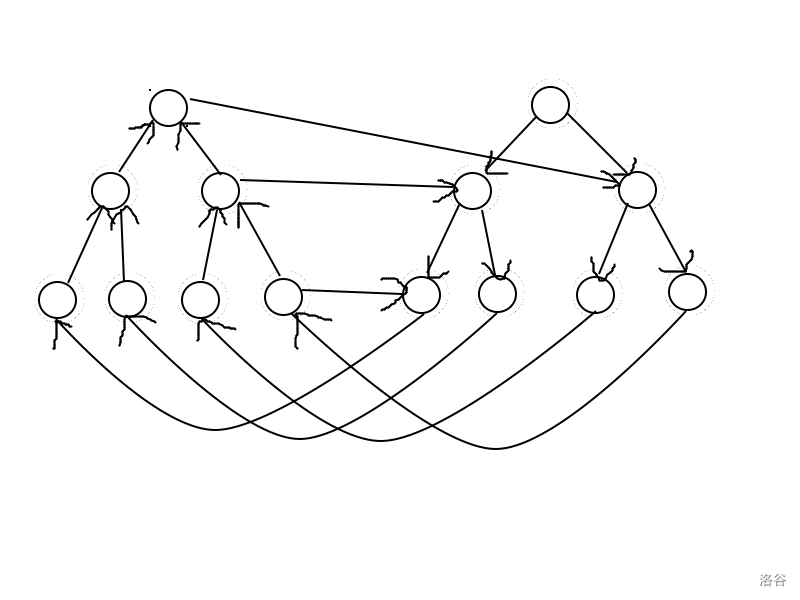
如图，所以我们甚至不需要建线段树，只需要线段树的节点编号就可以了。

还有，这道题卡 \(spfa\) ，甚至多带一个 \(log\) 都能被卡，伤心……

代码如下：

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+5;
int n,m,s;
int opt,u,v,l,r,w;
struct Edge{int nxt,to,val;}e[N<<6];
int fir[N<<4],size=0;
void add(int u,int v,int w)
{
	e[++size]=Edge{fir[u],v,w};
	fir[u]=size;
	return ;
}
void build(int p,int l,int r)
{
	if(l==r)
	{
		add(p+(N<<2),p,0);
		return ;
	}
	add(p<<1,p,0),add(p<<1|1,p,0);
	add(p+(N<<2),(p<<1)+(N<<2),0);
	add(p+(N<<2),(p<<1|1)+(N<<2),0);
	int mid=(l+r)>>1;
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r);
	return ;
}
void find(int p,int l,int r,int x,int y,vector<int> &now)
{
	if(x<=l&&r<=y)
	{
		now.push_back(p);
		return ;
	}
	int mid=(l+r)>>1;
	if(x<=mid)
	find(p<<1,l,mid,x,y,now);
	if(y>=mid+1)
	find(p<<1|1,mid+1,r,x,y,now);
	return ;
}
int dis[N<<4];
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;
bool vis[N<<4];
void dijkstra()
{
	for(int i=0;i<(N<<3);++i)
	dis[i]=1e18+7;
	vector<int> now;find(1,1,n,s,s,now);
	dis[now[0]]=0;
	q.push(make_pair(dis[now[0]],now[0]));
	while(!q.empty())
	{
		while(!q.empty()&&vis[q.top().second])
		q.pop();
		if(q.empty())
		break;
		pair<int,int> tmp=q.top();q.pop(),vis[tmp.second]=true;
		for(int i=fir[tmp.second];i;i=e[i].nxt)
		{
			if(dis[e[i].to]>tmp.first+e[i].val)
			{
				dis[e[i].to]=tmp.first+e[i].val;
				q.push(make_pair(dis[e[i].to],e[i].to));
			}
		}
	}
	return ;
}
signed main()
{
	cin>>n>>m>>s;
	build(1,1,n);
	for(int i=1;i<=m;++i)
	{
		scanf("%lld",&opt);
		if(opt==1)
		{
			scanf("%lld%lld%lld",&u,&v,&w);
			vector<int> a;find(1,1,n,u,u,a);
			vector<int> b;find(1,1,n,v,v,b);
			add(a[0],b[0]+(N<<2),w);
		}
		if(opt==2)
		{
			scanf("%lld%lld%lld%lld",&u,&l,&r,&w);
			vector<int> a;find(1,1,n,u,u,a);
			vector<int> b;find(1,1,n,l,r,b);
			for(int i=0;i<a.size();++i)
			{
				for(int j=0;j<b.size();++j)
				add(a[i],b[j]+(N<<2),w);
			}
		}
		if(opt==3)
		{
			scanf("%lld%lld%lld%lld",&v,&l,&r,&w);
			vector<int> a;find(1,1,n,l,r,a);
			vector<int> b;find(1,1,n,v,v,b);
			for(int i=0;i<a.size();++i)
			{
				for(int j=0;j<b.size();++j)
				add(a[i],b[j]+(N<<2),w);
			}
		}
	}
	dijkstra();
	for(int i=1;i<=n;++i)
	{
		vector<int> now;find(1,1,n,i,i,now);
		if(dis[now[0]]==1e18+7) printf("-1 ");
		else printf("%lld ",dis[now[0]]);
	}
	printf("\n");
	return 0;
}