分层图
分层图
讲真的...感觉有点像那么一点点的种类并查集
简单来说,就是把一个图分成很多层,然后对图进行一些处理
比较模板一点的东西就是直接在分层图上跑最短路,这个时候就涉及到了很多决策,每一个决策能进行一些特殊的操作,比如让某条边免费(边权为0,不是把边切掉),让某条边花费减半之类的,这个时候就可以用分层图了
然后讲讲分层图的具体实现。首先就是空间这个东西,你要有k个决策,那么你就要开k+1倍的空间,每一层空间涉及到一个决策,。然后对于第一层的图,还是正常的直接建图,数据怎么搞你就怎么搞。对于第二层及以上的图,将这一层和下一层连一条有向边,表示你这一次的决策
那么通过以上的一些分析,对于一个含n个点的图,我们需要开 n+k * n 的空间,即 n+k * n 个点,举个例子吧,大概就是以下这张图(这个图照搬我同桌的)

具体的实现方法,以例题为例(四倍经验爽不爽,会把四道题都放在下面的)
这道题非常模板啊(之后那三道题也非常模板),就是对一个非常正常的图,你需要求一个最短路,但是在你走的时候,你可以对你走的一些边进行一次改变,把这条边的边权改为之前的二分之一,那么这个时候最朴素的想法就是求一个最短路,并且记录这条最短路的边,对这些边排个序,把最长的几条边改了就行了,就有了以下程序(最短路这里就不讲了)
#include <bits/stdc++.h>
using namespace std;
int n,m,k,u,v,t,tot,ans;
int dis[20010],vis[20010],head[20010];
priority_queue<int> qq;
priority_queue<pair<int,int> > q;
struct node {
int to,net,val;
} e[20010];
struct nodes {
int id,num;
} pre[20010];
inline void add(int u,int v,int w) {
e[++tot].to=v;
e[tot].val=w;
e[tot].net=head[u];
head[u]=tot;
}
inline void dijkstra() {
memset(dis,20050206,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[1]=0;
q.push(make_pair(0,1));
while(!q.empty()) {
int x=q.top().second;
q.pop();
if(vis[x]) continue;
vis[x]=1;
for(register int i=head[x];i;i=e[i].net) {
int v=e[i].to;
if(dis[v]>dis[x]+e[i].val) {
dis[v]=dis[x]+e[i].val;
pre[v].id=x;
pre[v].num=e[i].val;
q.push(make_pair(-dis[v],v));
}
}
}
}
int main() {
scanf("%d%d%d",&n,&m,&k);
for(register int i=1;i<=m;i++) {
scanf("%d%d%d",&u,&v,&t);
add(u,v,t);
add(v,u,t);
}
dijkstra();
int kk=n;
while(kk!=1) {
qq.push(pre[kk].num);
kk=pre[kk].id;
}
while(k--) {
if(qq.empty()) break;
ans+=qq.top()/2;
qq.pop();
}
if(qq.empty()) {
printf("%d",ans);
return 0;
}
while(!qq.empty()) {
ans+=qq.top();
qq.pop();
}
printf("%d",ans);
return 0;
}
那么如果你是这样写的,恭喜你有70分啦,你甚至会发现你连第一个点都是WA,那么举个例子为什么你会错呢?
以下这个图,你跑出来的最短路应该是
1 -> 4 -> 5 -> 3 决策一次之后为18
然而另一条路应该是
1 -> 2 -> 3 决策一次之后为17
那这样你就错辽
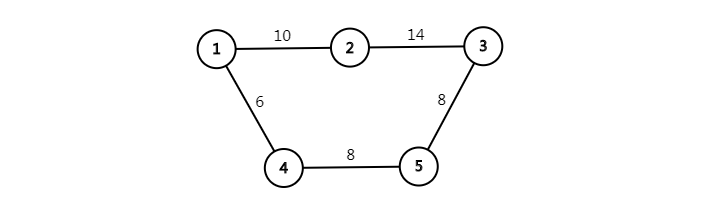
那么这样的话,就应该用分层图来做,那么直接看代码
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e4+50;
int n,m,k;
int head[MAXN*50],tot;
struct node{
int net,to,w;
}e[MAXN*50];
int d[MAXN*50];
bool v[MAXN*50]; //注意要多开k倍
void add(int u,int v,int w){
e[++tot].to=v;
e[tot].net=head[u];
e[tot].w=w;
head[u]=tot;
} //非常正常地村边
priority_queue< pair<int,int> > q;
void dij(int s){
fill(d,d+MAXN*50,20040915); //memset只能赋初值为0或-1,其他值应该是fill,不怎么了解的最好就用memset
memset(d,0x3f,sizeof d);
memset(v,false,sizeof v);
d[s]=0;
q.push(make_pair(0,s));
while(!q.empty()){
int x=q.top().second;
q.pop();
if(v[x]==true) continue;
v[x]=true;
for(register int i=head[x];i;i=e[i].net){
int y=e[i].to,z=e[i].w;
if(d[y]>d[x]+z){
d[y]=d[x]+z;
q.push(make_pair(-d[y],y));
}
}
}
} //非常正常的最短路
int main(){
scanf("%d%d%d",&n,&m,&k);
for(register int i=1;i<=m;i++){
int a,b,t;
scanf("%d%d%d",&a,&b,&t);
add(a,b,t);
add(b,a,t); //双向变
for(register int j=1;j<=k;j++){
add(a+j*n,b+j*n,t);
add(b+j*n,a+j*n,t); //在每一层中建一个正常地边
add(a+(j-1)*n,b+j*n,t/2);
add(b+(j-1)*n,a+j*n,t/2); //在下一层连一条单向边,表示你的决策,边权视题目而定
}
}
for(register int i=1;i<=k;i++) add(n+(i-1)*n,n+i*n,0); //终点单独连边
dij(1); //跑最短路
cout<<d[n+k*n]; //k个决策,所有第k+1层才是最后的答案
return 0;
}
那么这道题你就成功地A掉了啊,那么接下来就是非常快乐的三倍经验时刻,我会把题目挂在下面(题目不完全相同,但是只是略微区别),然后对于分层图还有另外一种做法,对于空间要求来说更低,蒟蒻暂且不会,之后应该会更吧
P2939 [USACO09FEB]Revamping Trails G
P1948 [USACO08JAN]Telephone Lines S
滚回来继续更新,开篇放题
一道紫题,还是挺难得,无论是思维难度还是编程难度(没办法判断太多了)
首先说明,我的一些思想和程序是参照了此篇题解之后的
首先看到题目的最小费用,以及一些操作,是可以想到搜索或者是最短路的,但是仔细想一番之后,其实是有点难度的。我们消耗的有两个东西,一是花费(就是钱),二是油
答案求最小花费,那我们最短路中建图时,就考虑以每次花费为边权,两个端点就是坐标就可以了。但是剩下一个油怎么办呢,就可以考虑用分层图的思想
我们分层分的是使用油的状态:满油(第1层),消耗了1个单位的油(第2层),消耗了2个单位的油(第3层)······所有油都消耗完了,那么我们就需要分\(k+1\)层图
那么确定如何分层和根据什么东西分层之后,如何建图呢?
- 对于每一个点
我们枚举走到当前点的所有使用油的情况,并向下一层连一条花费为0的边
- 当我们遇到了一个加油站
我们枚举走到这一个加油站的使用油的情况,很明显只需要枚举第\(2\)层~第\(k+1\)层,然后对当前点建一条指向该加油站边权为\(a\)的边,表示你加油这个状态
再由这个点,向下一层连一条花费为0的边
- 考虑自己修建加油站的情况
枚举每一种使用油的情况,建一条边权为\(a+c\)的边
然后直接跑最短路就可以了,但是因为这道题还要涉及到一些细节的问题,我直接放在程序里面讲
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e6+51;
int n,k,a,b,c;
int hh; //这是一个辅助变量
struct node{
int to,net,w;
}e[MAXN]; //正常的连边
int head[MAXN],tot;
void add(int x,int y,int z,int xx,int yy,int zz,int w){
int s=hh*(z-1)+(x-1)*n+y;
int t=hh*(zz-1)+(xx-1)*n+yy;
//这个地方和之前把二维转化为一维不太一样
//因为涉及到使用油的情况,有点像一个三维的图
//之前的公式是 (x-1)*n+y
//这里应该是 z*n*n+(x-1)*n+y
e[++tot].w=w;
e[tot].to=t;
e[tot].net=head[s];
head[s]=tot;
}
int oil;
int d[MAXN];
bool v[MAXN];
queue<int>q;
void spfa(int s){ //正常的SPFA
for(register int i=1;i<=hh*(k+1);i++){ //看上面的公式,这里应该有n*n*(k+1)个点
d[i]=220040915;
v[i]=false;
}
d[s]=0;
v[s]=true;
q.push(s);
while(!q.empty()){
int x=q.front();
q.pop();
v[x]=false;
for(register int i=head[x];i;i=e[i].net){
int y=e[i].to,z=e[i].w;
if(d[y]>d[x]+z){
d[y]=d[x]+z;
if(v[y]==false){
v[y]=true;
q.push(y);
}
}
}
}
}
int main(){
scanf("%d%d%d%d%d",&n,&k,&a,&b,&c);
hh=n*n; //懒得写n*n了,多写个hh
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
scanf("%d",&oil);
for(int l=1;l<=k;++l) add(i,j,l,i,j,l+1,0); //向下一层建一条边
if(oil){ //如果是加油站
for(int l=2;l<=k+1;++l) add(i,j,l,i,j,1,a); //强行给你把油加满,花费a块钱
//向四个方向建边
//因为已经加满油了,所以固定的建第一层到第二层的边就可以了
if(i<n) add(i,j,1,i+1,j,2,0);
if(j<n) add(i,j,1,i,j+1,2,0);
//注意往上和往左走是要给钱的
if(i>1) add(i,j,1,i-1,j,2,b);
if(j>1) add(i,j,1,i,j-1,2,b);
}else{
//枚举每一种用油的情况
for(int l=1;l<=k;++l){ //不循环到k+1,你不可能油空了还能用吧
//同上
if(i<n) add(i,j,l,i+1,j,l+1,0);
if(j<n) add(i,j,l,i,j+1,l+1,0);
if(i>1) add(i,j,l,i-1,j,l+1,b);
if(j>1) add(i,j,l,i,j-1,l+1,b);
}
for(int l=2;l<=k+1;++l) add(i,j,l,i,j,1,a+c);
//建一个加油站,不从1开始,是因为直接加满了
}
}
}
spfa(1);
int ans=220040915;
for(int i=1;i<=k+1;++i) ans=min(ans,d[hh*i]); //枚举到最后的终点时,每一种用油的情况,花费最下的一种
cout<<ans;
return 0;
}
P3119 [USACO15JAN]Grass Cownoisseur G
和大佬同桌一起做的,感谢大佬对我的指导,贴一下Ta的博客
我的最开始的思路就是DFS,因为想着DFS可以枚举往回走的情况,然而我发现题目读错了。逆行相当于建一条反向边,但是并没有规定必须在走过的路中逆行,你可以提前建这样一条反向边
然而我以为只能在走过的路中逆行,完美爆0
过了很久之后把Tarjan的很多题都刷了,然后找到了这道题,发现我们完全通过缩点把一些环缩成一个点,然后继续处理
如果没有这个逆行,我会想着跑最长路(SPFA或者拓扑排序),但是对于这个逆行,即建一条反向边,应该如何处理呢
没错,分层图。我记得我在我的博客中单独写了一篇文章讲分层图,但是放在那里面的题比较入门,建议先学一学。因为只需要建一条反向边,所以我们就只需要两层图就够了
记住,在分层图中,我们新建的一层图是不会改变原图的结构的,后面的每一层图想较于第一层图(原图)来说,是一模一样的建边,但是对于这个逆行,对于当前节点 \(i\),到达节点 \(j\) ,应该建一条 \(j\) 到 \(i+cnt\) 的边,然后跑最长路,整个题就解决了
#include <bits/stdc++.h>
using namespace std;
int n,m,x[520010],y[520010],ti,tot,cnt,ans,top,q[520010];
int dfn[520010],low[520010],dis[520010],vis[520010],num[520010],fir[520010],head[520010];
struct node {
int to,net,val;
} e[5200010];
inline void add(int u,int v,int w) {
e[++tot].to=v;
e[tot].val=w;
e[tot].net=head[u];
head[u]=tot;
}
inline void tarjan(int x) {
dfn[x]=low[x]=++ti;
q[++top]=x;
vis[x]=1;
for(register int i=head[x];i;i=e[i].net) {
int v=e[i].to;
if(!dfn[v]) {
tarjan(v);
low[x]=min(low[x],low[v]);
}
else {
if(vis[v]) low[x]=min(low[x],dfn[v]);
}
}
if(dfn[x]==low[x]) {
++cnt;
while(q[top+1]!=x) {
fir[q[top]]=cnt;
num[cnt]++;
vis[q[top]]=0;
top--;
}
}
}
inline void spfa(int s) {
for(register int i=1;i<=520000;i++) {
vis[i]=0;
dis[i]=-1;
}
queue<int> q;
vis[s]=1;
dis[s]=0;
q.push(s);
while(!q.empty()) {
int x=q.front();
q.pop();
vis[x]=0;
for(register int i=head[x];i;i=e[i].net) {
int v=e[i].to;
if(dis[v]<dis[x]+e[i].val) {
dis[v]=dis[x]+e[i].val;
if(!vis[v]) {
vis[v]=1;
q.push(v);
}
}
}
}
}
int main() {
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;i++) {
scanf("%d%d",&x[i],&y[i]);
add(x[i],y[i],0);
}
for(register int i=1;i<=n;i++) {
if(!dfn[i]) tarjan(i);
}
tot=0;
memset(head,0,sizeof(head));
for(register int i=1;i<=m;i++) {
if(fir[x[i]]==fir[y[i]]) continue;
add(fir[x[i]],fir[y[i]],num[fir[x[i]]]);
add(fir[x[i]]+cnt,fir[y[i]]+cnt,num[fir[x[i]]]);
add(fir[y[i]],fir[x[i]]+cnt,num[fir[y[i]]]);
//注意分层图的建边,这题只需要两层图
}
spfa(fir[1]); //在缩完点之后的图中跑最长路
printf("%d",dis[fir[1]+cnt]); //第二层图用来往回走
return 0;
}

