CF1720E Misha and Paintings 题解

神仙 2700。

首先统计出原数组中不同元素个数记作 \(cnt\)，如果 \(cnt\le k\) 说明元素个数不够，由于一次只能加一个颜色因此答案就是 \(k-cnt\)。

然后接下来要证明一个结论：答案上限为 2。

证明：

下面都以左上角为 \((1,1)\) 为条件证明，对于左上角不为 \((1,1)\) 的情况证明类似。

考虑每次以左上角 \((1,1)\) 为正方形顶点，边长一步步扩大，如下图（绿色部分）：

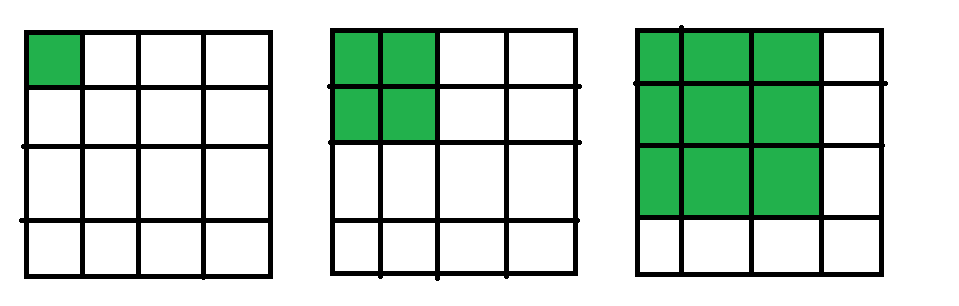
设正方形右下角 \((i,i)\)，那么我们从 \((i+1,i+1)\) 开始，每次往上往左覆盖一个（但是不与之前的正方形重合），如下图（蓝色部分，黑色部分为重叠）：

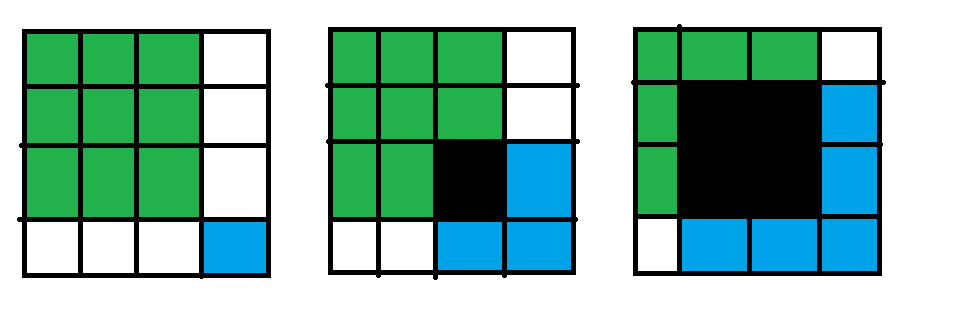
这就是两次覆盖，下面钦定这两次覆盖都使用剩余白色部分中没有的颜色覆盖。

注意到第一次覆盖之后，如果白色部分颜色种类为 \(k\) 或者是 \(k-1\)，那么我们可以使绿色部分颜色覆盖为原来就有的颜色（对应 \(k\)）或是一种新颜色（对应 \(k-1\)），此时答案为 1。该条件也是答案为 1 的充要条件。

如果白色部分颜色种类大于 \(k\)，我们需要第二次覆盖，注意到第二次覆盖从 \(1\times1\to2\times2\to...\) 时，每次扩展两格，则颜色可能减少 0,1,2。

由于我们需要第二次覆盖，因此蓝色+白色部分原颜色种类个数一定大于 \(k\)，因此我们可以证明过程中一定会有一组满足条件的绿色和蓝色矩形覆盖方案，使得白色部分为 \(k\) 或者 \(k-1\)，若为 \(k\) 那么就覆上两个相同且有的颜色，若为 \(k-1\) 那么一个覆有的一个覆没有的，特别的有人会问能不能 \(k-2\) 然后覆盖两个新的，但该情况其实可以归约到 \(k\) 和 \(k-1\) 的情况。

如果白色部分颜色种类小于 \(k-1\)，此时我们需要缩短正方形边长，因为正常情况下你已经没法做到再覆盖一次使得颜色种类为 \(k\)，最好情况就是类似于白色新覆盖一个，白色里面新覆盖一个可以做到两次，然而缩短边长同样可以两次：

考虑一种临界情况，边长为 \(i\) 时白色部分颜色种类小于 \(k-1\)，边长为 \(i-1\) 时白色部分颜色种类 \(>k\)（等于 \(k\) 或 \(k-1\) 时答案就是 1，上面已经证明），然后我们使用蓝色矩形尽可能覆盖边长为 \(i-1\) 的正方形，那么只会剩下左下角右上角两个格子没有覆盖。

注意到由于边长为 \(i\) 和 \(i-1\) 时白色部分颜色种类分别小于 \(k-1\) 和大于 \(k\)，因此这里面存在至少两种颜色跨度，无论这两种颜色是不是左上角右上角独有的，都可以得知蓝色矩形覆盖过程中会出现白色部分为 \(k\) 或者 \(k-1\) 的情况，因为尽可能覆盖时白色区域颜色种类最小也是 \(k-1\) 种。

上述除了证明白色部分颜色种类小于 \(k-1\) 缩短边长就可以之外，同时也证明了必然存在方案。

这样就证明了结论：答案上界为 2。

现在只需要考虑答案为 1 的情况（答案为 0 已经在 \(cnt\le k\) 中处理了），满足该情况就需要存在一个正方形满足其余部分颜色个数为 \(k\) 或 \(k-1\)，考虑先枚举长度 \(len\)，预处理 \(sum_{i,j}\) 表示长度为 \(len\) 时 \((i,j)\) 为左上角的正方形内完全包含多少种颜色，也就是 \(cnt-sum_{i,j}\) 为其余部分颜色个数。

为做到这一点，考虑预处理覆盖每个颜色的最小矩形 \((x1,y1),(x2,y2)\)，由于枚举长度为 \(len\)，我们可以知道对于每个颜色，有哪些正方形能覆盖到这个颜色，对这些正方形左上角顶点加一，即矩形加 1，这可以二维差分然后二位前缀和解决。

处理完 \(sum_{i,j}\) 后，只需要知道有无 \(cnt-sum_{i,j}\) 为 \(k\) 或 \(k-1\) 即可。

GitHub：CodeBase-of-Plozia

Code：

/*
========= Plozia =========
	Author:Plozia
	Problem:CF1720E Misha and Paintings
	Date:2022/9/20
========= Plozia =========
*/

#include <bits/stdc++.h>
typedef long long LL;

const int MAXN = 500 + 5;
int n, k, a[MAXN][MAXN], sum[MAXN][MAXN], cnt, fir[MAXN * MAXN][2], sec[MAXN * MAXN][2];
bool book[MAXN * MAXN];

int Read()
{
	int sum = 0, fh = 1; char ch = getchar();
	for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
	for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = (sum << 3) + (sum << 1) + (ch ^ 48);
	return sum * fh;
}

int main()
{
	n = Read(), k = Read();
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= n; ++j)
			book[a[i][j] = Read()] = 1;
	for (int i = 1; i <= n * n; ++i) cnt += book[i];
	if (cnt <= k) { printf("%d\n", k - cnt); return 0; }
	memset(fir, 0x7f, sizeof(fir));
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= n; ++j)
		{
			fir[a[i][j]][0] = std::min(fir[a[i][j]][0], i);
			fir[a[i][j]][1] = std::min(fir[a[i][j]][1], j);
			sec[a[i][j]][0] = std::max(sec[a[i][j]][0], i);
			sec[a[i][j]][1] = std::max(sec[a[i][j]][1], j);
		}
	int flag = 0;
	for (int len = 1; len <= n; ++len)
	{
		for (int i = 1; i <= n; ++i) for (int j = 1; j <= n; ++j) sum[i][j] = 0;
		for (int i = 1; i <= n * n; ++i)
		{
			if (!book[i]) continue ;
			if (len < std::max(sec[i][0] - fir[i][0], sec[i][1] - fir[i][1])) continue ;
			int Line = sec[i][0] - fir[i][0] + 1, Col = sec[i][1] - fir[i][1] + 1;
			int r1 = std::max(1, fir[i][0] - (len - Line)), c1 = std::max(1, fir[i][1] - (len - Col));
			int r2 = std::min(n - len + 1, fir[i][0]), c2 = std::min(n - len + 1, fir[i][1]);
			++sum[r1][c1]; --sum[r2 + 1][c1]; --sum[r1][c2 + 1]; ++sum[r2 + 1][c2 + 1];
		}
		for (int i = 1; i <= n; ++i)
			for (int j = 1; j <= n; ++j)
				sum[i][j] = sum[i][j] + sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1];
		for (int i = 1; i <= n; ++i)
			for (int j = 1; j <= n; ++j)
				if (cnt - sum[i][j] == k || cnt - sum[i][j] == k - 1) flag = 1;
	}
	if (flag == 1) printf("1\n");
	else printf("2\n");
	return 0;
}