数据结构专题 - 学习笔记：线段树分治
1. 前言
线段树分治，是一种数据结构，常用来离线维护一张图的连通性。
大致来讲，这张图的边会在一段时间内出现，别的时间消失，然后会有一些询问，线段树分治解决的就是这样的问题。
2. 详解
模板题：P5787 二分图 /【模板】线段树分治，下面假定 \(n,m\) 同阶。
首先考虑一个暴力做法：对于每一个时间，我们建图然后染色，这样复杂度是 \(O(n^2k)\) 的。
当然另一种判定二分图的方式是扩展域并查集，就是对每个点建立两个点 \(x\) 和 \(x+n\)，对于每条边 \((x,y)\) 合并 \(x,y+n\) 和 \(x+n,y\)，如果有一条边 \((x',y')\) 满足 \(x',y'\) 在一个集合内那么就不是二分图，否则就是二分图。
利用并查集做法复杂度照样是 \(O(n^2k)\) 的，不过并查集有一个优势是在不进行路径压缩的情况下我们可以撤销操作。
注意到每条边覆盖的是一段时间，因此我们考虑在时间轴上建线段树，然后将每条边插入到其所对应的区间中。
插入方法类似于线段树的区间修改，考虑往下递归，当递归到的节点被完全包含于修改区间的时候在这个节点插入这条边，然后不往下递归，我们需要某个点的连边信息时从根节点直接搜到叶节点，中途的点存的边不断插入即可，如下：
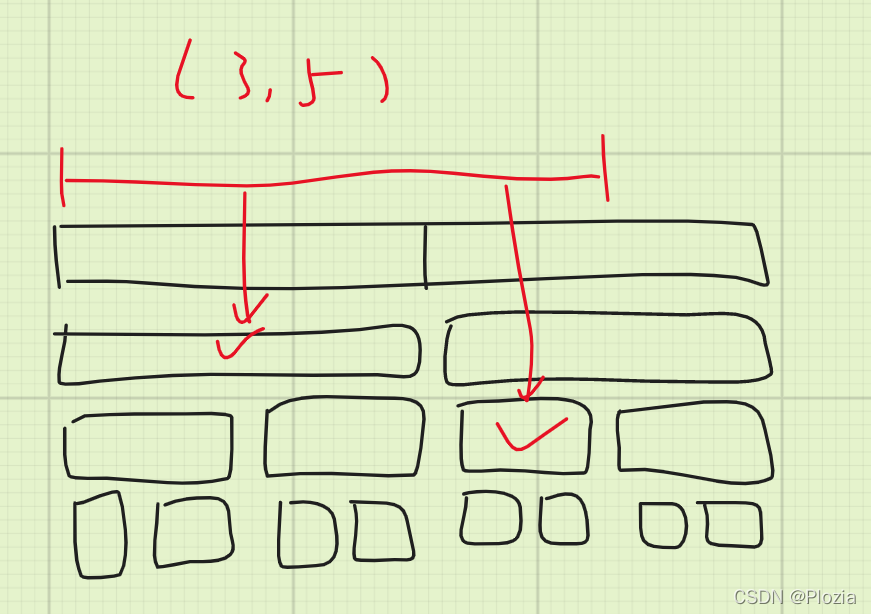
\((3,5)\) 这条边被插入到了上图打勾的两个区间内。
然后考虑 dfs 整棵树，往下搜的时候加入当这个节点所存的边，用扩展域并查集判定二分图，如果一个区间判定出不是二分图则其维护的时间段全都要打上标记。
向下搜索就是不断加边，至于回溯，考虑用一个栈维护加边操作，回溯时弹栈还原并查集即可。注意在这种做法下是不能路径压缩的，因此必须采用按秩合并，而且是用高度合并而不是用子树大小合并，因为并查集查询的复杂度看的是高度不是子树大小。
注意模板题对时间轴的处理。
GitHub：CodeBase-of-Plozia
Code：
/*
========= Plozia =========
Author:Plozia
Problem:P5787 二分图 /【模板】线段树分治
Date:2022/3/27
========= Plozia =========
*/
#include <bits/stdc++.h>
using std::vector;
using std::stack;
typedef long long LL;
const int MAXN = 1e5 + 5;
int n, m, k, cnt, ans[MAXN], fa[MAXN << 1], Height[MAXN << 1];
struct node { int x, y, l, r; } Edge[MAXN << 1];
struct STA { int x, y, h; } ;
struct SgT
{
vector <int> E;
}tree[MAXN << 2];
stack <STA> sta;
int Read()
{
int sum = 0, fh = 1; char ch = getchar();
for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = sum * 10 + (ch ^ 48);
return sum * fh;
}
int Max(int fir, int sec) { return (fir > sec) ? fir : sec; }
int Min(int fir, int sec) { return (fir < sec) ? fir : sec; }
int gf(int x) { while (fa[x] != x) x = fa[x]; return x; }
void Insert(int p, int l, int r, int Num, int lp, int rp)
{
if (lp >= l && rp <= r) { tree[p].E.push_back(Num); return ; }
int mid = (lp + rp) >> 1;
if (l <= mid) Insert(p << 1, l, r, Num, lp, mid);
if (r > mid) Insert(p << 1 | 1, l, r, Num, mid + 1, rp);
}
void Merge(int x, int y)
{
x = gf(x), y = gf(y);
if (Height[x] > Height[y]) std::swap(x, y);
sta.push((STA){x, y, Height[x] == Height[y]});
fa[x] = y; Height[y] += (Height[x] == Height[y]);
}
void dfs(int p, int lp, int rp)
{
int cnt = 0, flag = 0;
for (int i = 0; i < tree[p].E.size(); ++i)
{
int x = Edge[tree[p].E[i]].x, y = Edge[tree[p].E[i]].y;
if (gf(x) == gf(y))
{
for (int j = lp; j <= rp; ++j) ans[j] = 1;
flag = 1; break ;
}
if (gf(x) != gf(y + n)) Merge(x, y + n), ++cnt;
if (gf(y) != gf(x + n)) Merge(y, x + n), ++cnt;
}
if (lp < rp && !flag) { int mid = (lp + rp) >> 1; dfs(p << 1, lp, mid); dfs(p << 1 | 1, mid + 1, rp); }
while (cnt--)
{
STA tmp = sta.top(); sta.pop();
fa[tmp.x] = tmp.x; Height[tmp.y] -= tmp.h;
}
}
int main()
{
n = Read(), m = Read(), k = Read();
for (int i = 1; i <= m; ++i)
{
int x = Read(), y = Read(), l = Read(), r = Read();
Edge[i] = (node){x, y, l + 1, r};
if (l + 1 <= r) Insert(1, l + 1, r, i, 1, k);
}
for (int i = 1; i <= n * 2; ++i) fa[i] = i, Height[i] = 1;
dfs(1, 1, k);
for (int i = 1; i <= k; ++i) puts((ans[i] == 0) ? ("Yes") : ("No"));
return 0;
}
3. 总结
线段树分治将边拆解到区间里面，利用一些可撤销的数据结构进行 dfs 统计答案。
注意线段树分治是个离线算法，不能在线。
