图论专题-学习笔记:Prufer 序列
1. 前言
Prufer 序列,是一种用来描述树的序列,一般用于一些树上度数统计的题。
注意作者是 OIer,考虑到 Prufer 序列在 OI 里面的应用等,本篇文章只讲述 的求法。
2. 详解
设有一棵 点的树,则这个 点的树和一个长度为 的 Prufer 序列是一一对应的,下面给出树与 Prufer 序列的互相转换方式。
2.1 树 Prufer 序列
转换方式如下:
- 从当前树上所有度数为 1 的点中取出编号最小的点,将与其直接连接的边加入 Prufer 序列中。
- 删除选出的这个点,同时被加入 Prufer 序列的点度数要减一,如果该点度数变为 1 那么这个点就有可能被取出。
- 重复该操作直到只剩下两个点,此时算法结束,Prufer 序列长度为 。
使用堆可以很方便的完成这一系列操作,复杂度 。
这里放上一张图,来自参考资料中的 OI - Wiki 中的图片(不确定他们这张图是哪来的,反正我从这里引用过来):
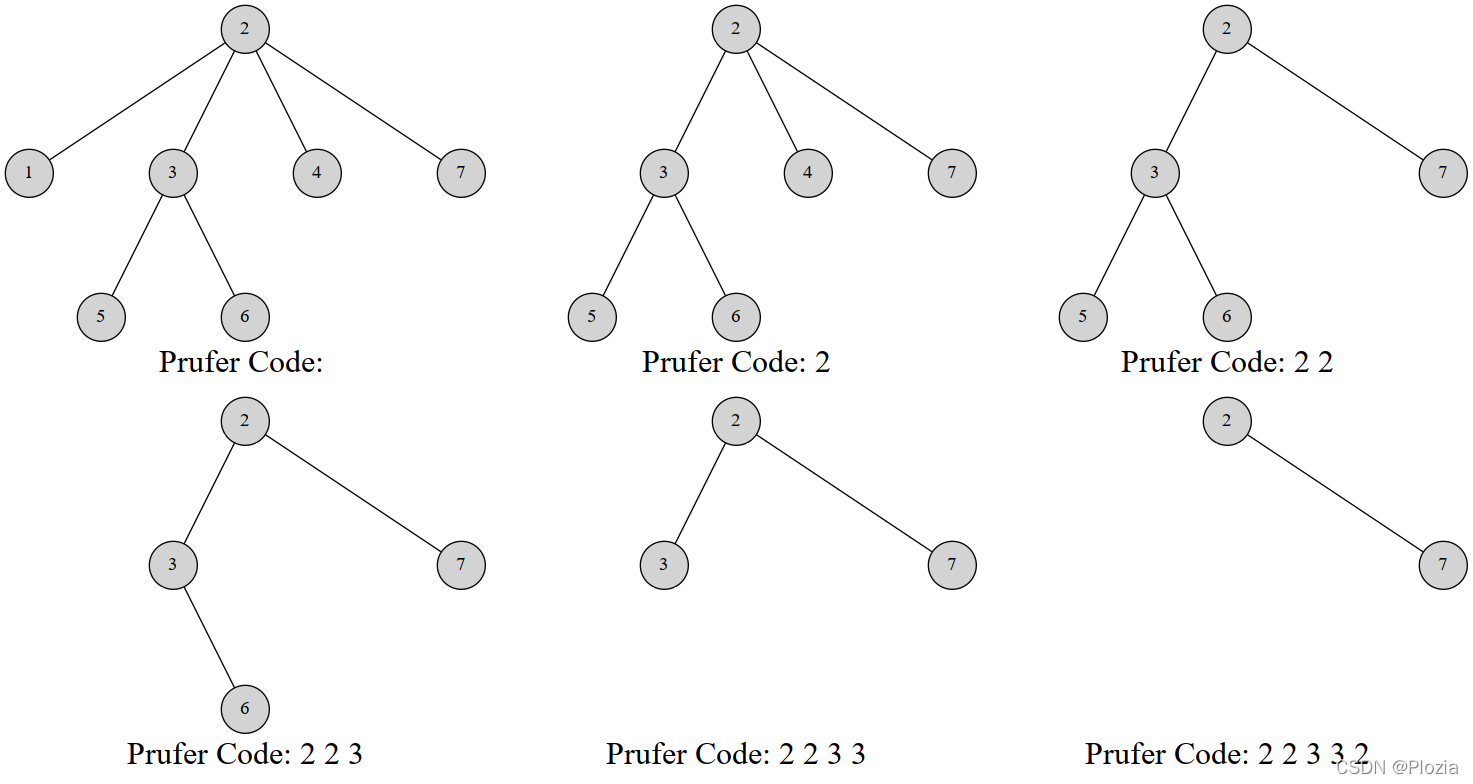
参考代码如下,其中 表示 的父亲,代码中以 为根节点。
void TreeToPrufer()
{
for (int i = 1; i < n; ++i) fa[i] = Read(), ++d[i], ++d[fa[i]];
priority_queue <int> q;
for (int i = 1; i <= n; ++i) if (d[i] == 1) q.push(-i);
for (int i = 1; i <= n - 2; ++i)
{
int x = -q.top(); q.pop();
Prufer[++Prufer[0]] = fa[x]; --d[fa[x]];
if (d[fa[x]] == 1) q.push(-fa[x]);
}
}
实际上,根据构造方式,我们可以得出 Prufer 序列的两个性质:
- 号点在 Prufer 序列中出现的次数为 号点度数 - 1。
同时,构造完 Prufer 序列后原树只会剩下两个节点,其中一个一定是 。
2.2 Prufer 序列 树
仿照树 Prufer 序列的做法,可以得到如下方式:
- 根据 Prufer 序列和上文的一个性质,算出所有点度数。
- 枚举 ,设 为 Prufer 序列,每次取出当前未被删除且度数为一的编号最小的点,设为 ,将 与 连边然后删去 ,同时减小 的度数。
- 最后应当会剩下两个度数为 1 的点,其中一个一定是 ,将这两个点连起来即可。
照样使用堆来实现这一过程,复杂度 。
参考代码如下,这里采用了链式前向星连边,然后使用一遍 dfs 求出 。
void dfs(int now, int father)
{
fa[now] = father;
for (int i = Head[now]; i; i = Edge[i].Next)
{
int u = Edge[i].To;
if (u == father) continue ;
dfs(u, now);
}
}
void PruferToTree()
{
for (int i = 1; i <= n - 2; ++i) Prufer[i] = Read(), ++d[Prufer[i]];
for (int i = 1; i <= n; ++i) ++d[i];
priority_queue <int> q;
for (int i = 1; i <= n; ++i) if (d[i] == 1) q.push(-i);
for (int i = 1; i <= n - 2; ++i)
{
int x = -q.top(); q.pop();
add_Edge(x, Prufer[i]); add_Edge(Prufer[i], x);
--d[Prufer[i]]; if (d[Prufer[i]] == 1) q.push(-Prufer[i]);
}
int p1 = -q.top(); q.pop();
add_Edge(p1, n); add_Edge(n, p1);
dfs(n, n);
}
3. 性质
首先前面提到过一个性质(设 号点度数为 ):
- 号点在 Prufer 序列中出现的次数为 。
然后利用 Prufer 序列,我们可以证明:
- 个点有标号无根树形态有 种。
以及一些需要度数的题都可以用 Prufer 序列求解。
这里再放上一个性质:对于给定 序列, 个点有标号无根树的种类有:
顺带一提,如果利用 Prufer 序列来造数据,随机情况下树高是 而不是 的。
4. 总结
Prufer 序列和树是一一对应的,与度数有很大的联系。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具