数据结构专题-学习笔记:K - D Tree
一些 Update
Update 2022/1/25:修正了 Delete 的代码。
1. 前言
本篇博文是作者学习 K - D Tree 时候的学习笔记。
K - D Tree,是一种实战运用中比较不错的数据结构,通常用来骗分或者是部分题的正解,然而复杂度玄学并且常数大。
那为啥还要学 K - D Tree?因为某些题专门卡你树套树或者 cdq 分治之类的,此时就需要 K - D Tree,而且 K - D Tree 好写好调。
2. 详解
首先我们要知道,K - D Tree 是一种维护高维空间内点集的数据结构, 表示维度,本文为了理解方便,取二维空间,本文的 统一指 行 列。
K - D Tree 一般有两种写法,一种是平衡树式 K - D Tree,每个节点都存一个点;另一种是线段树式 K - D Tree,只有叶子节点存点,这里只讲平衡树 K - D Tree 因为这个比较常见。
K - D Tree 的主要步骤有建树、插入 / 删除, 重构。
2.0 结构体
这里首先放一下结构体,可以先跳过,看后面代码的时候再返回来看。
struct kdtree
{
int ls, rs, Minx, Miny, Maxx, Maxy, val, lazy, Size;
#define ls(p) tree[p].ls // 左儿子
#define rs(p) tree[p].rs // 右儿子
#define Minx(p) tree[p].Minx // x 最小值
#define Maxx(p) tree[p].Maxx // x 最大值
#define Miny(p) tree[p].Miny // y 最小值
#define Maxy(p) tree[p].Maxy // y 最大值
#define val(p) tree[p].val // 点权和
#define lazy(p) tree[p].lazy // 删除懒标记
#define Size(p) tree[p].Size // 子树大小
}tree[MAXN];
注意上述中 ls(p),rs(p) 是必须的,lazy(p) 是删除操作必须的,Size(p) 是插入 / 删除操作必须的。
2.1 建树
首先我们需要明确一点,那就是 K - D Tree 本质上也是一棵平衡树,每个节点的编号就是点集中对应的点,比如这个点编号是 那么这个点对应的点就是 。
既然 K - D Tree 是棵平衡树,那么 K - D Tree 必然满足如下几个性质:
- 中序遍历就是原序列,注意这里的原序列是相对于点的位置而言的。
- 每个点记录的东西就是子树内所有点共同组成的,比如说点权和就是子树内所有点点权和。
- K - D Tree 需要平衡。
需要注意的是,严格意义上来讲每个点维护的其实是一个矩阵内的信息,这也就是上面结构体记录 Minx,Miny,Maxx,Maxy 的原因。
第三点是插入 / 删除要讨论的,第二步是 Update() 要讨论的,现在考虑如何建树。
我们其实可以仿照平衡树建树,把这个二维点集拎出来,然后通过一种类似于二分的方式建树。
回顾一下平衡树的建树过程,我们是在一个序列上二分的,设维护区间 那么我们将 和 分成两个传下去,这是在一个维度上划分的,并且第 个点的坐标就是 。
现在考虑 K - D Tree 在两个维度上划分,就有了两种划分方式:
- 轮换划分:每划分一次就转换划分标准,比如第一次按照 轴划分,第二次就换成 轴,第三次换回去,以此类推。
- 方差划分:算出当前需要维护的矩阵内的所有点 坐标方差和 坐标方差,哪个方差大就选哪个。
轮换划分写起来简便,方差划分效率高,当然实际上就是 7,8 行代码差距而已。
注意方差划分是需要使用 double 类型的,因此对于小数据跑不过轮换划分。
确定划分标准之后,将这一维的最中间那个点拉出来,就是当前子树的根节点,然后递归建树。
将过程具体模拟一下,下面采用的是方差划分,假设我们现在有这样一些点:
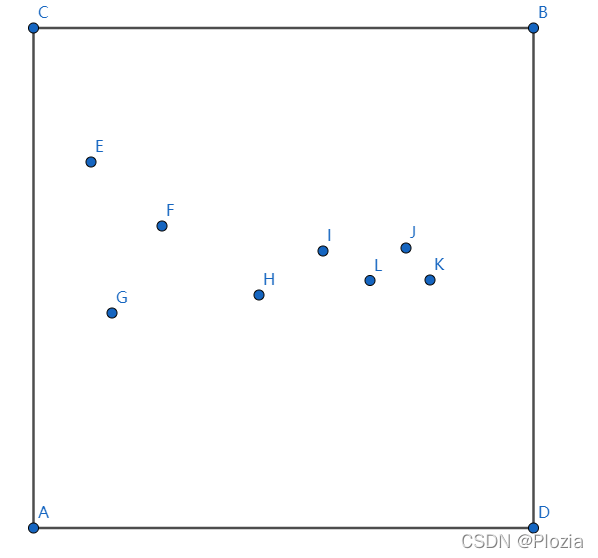
在矩阵 中,因 轴方差较大首先按照 轴划分,提取中间的点 维护 :
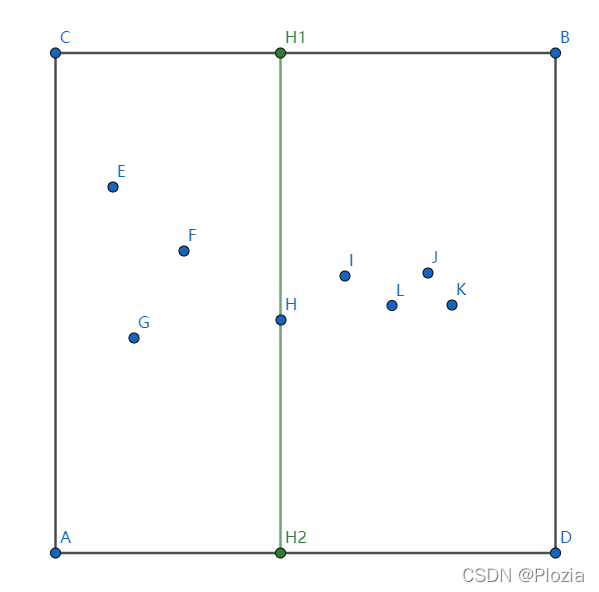
先看 ,注意到 轴方差较大按 轴划分,再看 ,注意到 轴方差较大按 轴划分,左边取 维护矩阵,右边取 维护矩阵:
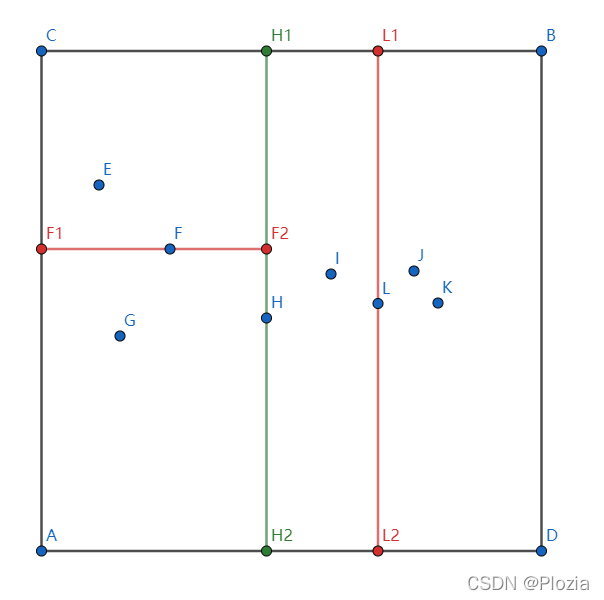
然后对 两个点维护一下,最后建的树应该是这样的:
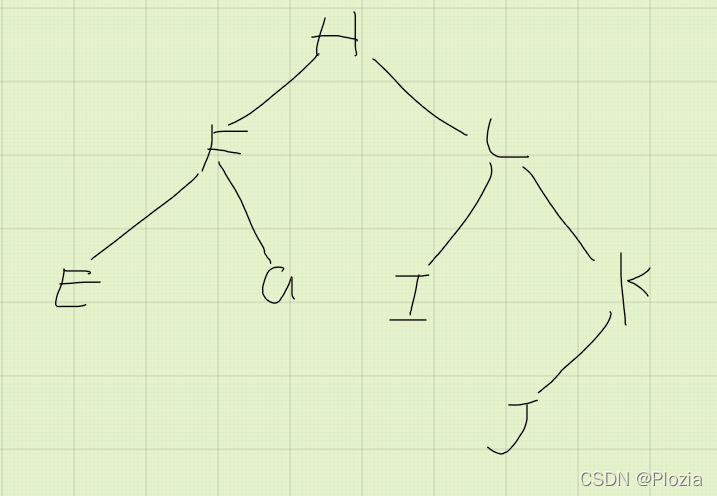
叶子节点地方可能会稍微有点不同,但是无伤大雅,依然是棵平衡树。
因此我们需要完成的有两件事,一件是算方差,另一件是找中间点。
算方差直接算就好了,找中间点相当于找第 大,利用 std::nth_element 可以找出第 大,顺便将小的移到左边,大的移到右边。
这一部分代码如下,其中 表示当前需要维护的点集的标号, 表示对应点按照哪个轴划分, 表示这个点的位置及其各种信息(如点权)。
int Build(int l, int r)
{
if (l > r) return 0;
int mid = (l + r) >> 1;
double avex = 0, avey = 0, valx = 0, valy = 0;
for (int i = l; i <= r; ++i)
avex += s[a[i]].x, avey += s[a[i]].y;
avex /= (r - l + 1), avey /= (r - l + 1);
for (int i = l; i <= r; ++i)
valx += (s[a[i]].x - avex) * (s[a[i]].x - avex),
valy += (s[a[i]].y - avey) * (s[a[i]].y - avey);
if (valx > valy)
std::nth_element(a + l, a + mid, a + r + 1, cmp1), d[a[mid]] = 1;
else
std::nth_element(a + l, a + mid, a + r + 1, cmp2), d[a[mid]] = 2;
ls(a[mid]) = Build(l, mid - 1); rs(a[mid]) = Build(mid + 1, r);
Update(a[mid]); return a[mid];
}
需要注意的是,对于一般的矩阵查询轮换划分平均下跑的较快,但是涉及到邻域查询这种乱搞的东西方差划分跑的比较快,但是还是建议写方差划分,因为其相对实现不错。
2.2 插入 / 删除
因为 K - D Tree 的划分方式每次不一样,所以我们没有办法像 Splay 那样旋转,又因为我们不能快速准确判断出当前点是属于哪个被维护的矩阵,而且即使能判断也会影响到该矩阵内很多点的划分依据,因此也不能像 FHQ Treap 的方法分裂合并。
所以不能旋转,不能分裂合并,似乎 K - D Tree 就没有什么好的维护方式了……吗?
这倒不一定,因为平衡树中有一个利器叫做替罪羊树。
首先回顾一下替罪羊树的建树和插入删除了:建树就是直接拎不多讲,插入是按照中序遍历为原序列插入的,删除是懒删除就是打个标记,不平衡了就拍扁重构。
跟 K - D Tree 很像对不对?实际上 K - D Tree 就是棵高维空间的替罪羊树。
由于我们之前已经记录下了每个点的划分依据,因此模仿替罪羊树,插入就是按照划分依据插入,删除就是找到点然后打懒标记假装删除然后自底向上维护。
插入代码如下:
void Insert(int &p, int x)
{
if (!p) { p = x; Update(p); return ; }
if (d[p] == 1)
{
if (s[x].x <= s[p].x) Insert(ls(p), x);
else Insert(rs(p), x);
}
else
{
if (s[x].y <= s[p].y) Insert(ls(p), x);
else Insert(rs(p), x);
}
Update(p); Check(p);
}
删除代码如下:
void Delete(int &p, int x)
{
if (!p) return ;
if (p == x) { lazy(p) = 1; Update(p); Check(p); return ; }
if (d[p] == 1)
{
if (s[x].x <= s[p].x) Delete(ls(p), x);
else Delete(rs(p), x);
}
else
{
if(s[x].y <= s[p].y) Delete(ls(p), x);
else Delete(rs(p), x);
}
}
2.3 重构
重构这一块也还是仿照替罪羊树,设一个 因子,当有一棵子树的大小超过了这棵树大小乘上 因子就拍扁重构,建议 取 之间的一个数,我一般取 。
这块的代码如下:
void Make_a(int p)
{
if (!p) return ;
Make_a(ls(p));
if (!lazy(p)) a[++cntn] = p;
Make_a(rs(p));
}
void Check(int &p)
{
if (Size(p) * alpha <= Size(ls(p)) || Size(p) * alpha <= Size(rs(p)))
{
cntn = 0; Make_a(p); p = Build(1, cntn);
}
}
注意这里的 Build() 是可以和建树的 Build() 一起用的,也就是为什么建树时要维护一个 。
2.4 时间复杂度 + 常数
目前理论证明 K - D Tree 各种操作的最优复杂度是 ,二维空间就是 ,还是挺优秀的一个复杂度,跟 比较接近吧,但是我不会证 /kk。
lxl:K - D Tree 常数大,是个没救的东西,不要去学它。
说一点我自己的理解吧:
首先要清楚 K - D Tree 常数确实有点大,这点是对的,但是根据其写法常数应该跟替罪羊树差不多,所以也不是特别大。
其次就是我们一般写的 K - D Tree 并不是理论最优复杂度的 K - D Tree,会多带一个 ,因为如果想要写理论最优复杂度的 K - D Tree 就会很烦,在 OI 中性价比不高,并且带上这个 之后常数似乎还变小了。
最后就是有些题确实 K - D Tree 能给出一个更加简明的解释,而且它能强制在线并且空间还小,因此有些出题人会利用这点只放 K - D Tree 而不放 cdq 和树套树过,下面就有。
综上所述,K - D Tree 其实还是蛮重要的一种数据结构,虽然 K - D Tree 没救是因为常数大而且很多时候能够被树套树和 cdq 替代,确实“没救”,但终究还是“有救”的,还是有学的必要。
我认为这个道理就跟替罪羊树要不要学一个道理吧,要学又没什么用,能够被 Splay 和 FHQ Treap 等替代,但是不要学又不行,因为思想非常关键。
上面只是我对 K - D Tree 是否要学的一些粗浅的认识,不喜轻喷,有误请指出。
3. 应用
先看一道模板题:P4357 [CQOI2016]K 远点对
这道题只有一个查询,因此我们考虑怎么写这个查询。
维护一个优先队列 q,里面至多装 k 个数表示从大到小 个最远距离,对于每一个点,我们都做一遍。
假设当前做的点是 ,我们需要将对 而言的前 个距离取出来,首先先跟当前搜到的节点 算一遍,如果更远就丢到优先队列里面。
然后因为我们知道每个点维护的矩阵(点集)是多少,把 Minx,Miny,Maxx,Maxy 取出来,计算一下当前这个要做的点与左右子树维护的矩阵的四个端点中的最大值,跟左子树做的是 ,跟右子树做的是 。
然后如果这两个里面只有一个比当前第 大要大,那么往那个子树搜就好了,但如果两个都比第 大要大,这个时候优先搜 较大的那一边,然后如果另外一边还是比第 大要大就再搜一遍。
这样做可以贪心理解,毕竟较大的那边更有可能出现第 大对吧。
注意这样做之后单次查询复杂度最坏还是 ,但是这不重要,因为本身写 K - D Tree 就不是为了拿满分的(跑得慢),而且对于大多数数据还是能过的。
GitHub:CodeBase-of-Plozia
Code:
/*
========= Plozia =========
Author:Plozia
Problem:P4357 [CQOI2016]K 远点对
Date:2022/1/13
========= Plozia =========
*/
#include <bits/stdc++.h>
using std::priority_queue;
typedef long long LL;
const int MAXN = 1e5 + 5;
int n, k;
struct node { LL x, y; } a[MAXN];
struct kdtree
{
int ls, rs;
LL Minx, Miny, Maxx, Maxy;
#define ls(p) tree[p].ls
#define rs(p) tree[p].rs
#define Minx(p) tree[p].Minx
#define Miny(p) tree[p].Miny
#define Maxx(p) tree[p].Maxx
#define Maxy(p) tree[p].Maxy
}tree[MAXN];
priority_queue < LL, std::vector <LL>, std::greater <LL> > q;
int Read()
{
int sum = 0, fh = 1; char ch = getchar();
for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = sum * 10 + (ch ^ 48);
return sum * fh;
}
LL Max(LL fir, LL sec) { return (fir > sec) ? fir : sec; }
LL Min(LL fir, LL sec) { return (fir < sec) ? fir : sec; }
LL Square(LL x) { return x * x; }
LL Calc(LL x, LL y) { return Max(Square(a[x].x - Minx(y)), Square(a[x].x - Maxx(y))) + Max(Square(a[x].y - Miny(y)), Square(a[x].y - Maxy(y))); }
bool cmp1(const node &fir, const node &sec) { return fir.x < sec.x; }
bool cmp2(const node &fir, const node &sec) { return fir.y < sec.y; }
void Update(int p)
{
Minx(p) = Maxx(p) = a[p].x; Miny(p) = Maxy(p) = a[p].y;
if (ls(p)) Minx(p) = Min(Minx(ls(p)), Minx(p)), Maxx(p) = Max(Maxx(ls(p)), Maxx(p)), Miny(p) = Min(Miny(ls(p)), Miny(p)), Maxy(p) = Max(Maxy(ls(p)), Maxy(p));
if (rs(p)) Minx(p) = Min(Minx(rs(p)), Minx(p)), Maxx(p) = Max(Maxx(rs(p)), Maxx(p)), Miny(p) = Min(Miny(rs(p)), Miny(p)), Maxy(p) = Max(Maxy(rs(p)), Maxy(p));
}
int Build(int l, int r)
{
if (l > r) return 0;
int mid = (l + r) >> 1;
double avex = 0, avey = 0, valx = 0, valy = 0;
for (int i = l; i <= r; ++i) avex += a[i].x, avey += a[i].y;
avex /= (r - l + 1), avey /= (r - l + 1);
for (int i = l; i <= r; ++i) valx += (a[i].x - avex) * (a[i].x - avex), valy += (a[i].y - avey) * (a[i].y - avey);
if (valx > valy) std::nth_element(a + l, a + mid, a + r + 1, cmp1);
else std::nth_element(a + l, a + mid, a + r + 1, cmp2);
ls(mid) = Build(l, mid - 1); rs(mid) = Build(mid + 1, r);
Update(mid); return mid;
}
void Ask(int l, int r, int x)
{
if (l > r) return ;
int mid = (l + r) >> 1; LL tmp = Square(a[mid].x - a[x].x) + Square(a[mid].y - a[x].y);
if (tmp > q.top()) { q.pop(); q.push(tmp); }
LL vall = Calc(x, ls(mid)), valr = Calc(x, rs(mid));
if (vall > q.top() && valr > q.top())
{
if (vall > valr) { Ask(l, mid - 1, x); if (valr > q.top()) Ask(mid + 1, r, x); }
else { Ask(mid + 1, r, x); if (vall > q.top()) Ask(l, mid - 1, x); }
}
else if (vall > q.top()) Ask(l, mid - 1, x);
else if (valr > q.top()) Ask(mid + 1, r, x);
}
int main()
{
n = Read(), k = Read() * 2;
for (int i = 1; i <= n; ++i) a[i].x = Read(), a[i].y = Read();
Build(1, n); for (int i = 1; i <= k; ++i) q.push(0);
for (int i = 1; i <= n; ++i) Ask(1, n, i);
printf("%lld\n", q.top()); return 0;
}
接下来看一下这道著名的例题:P4148 简单题。
这道题可以 K - D Tree,可以树套树,可以 cdq 分治,但是 20MB 空间卡掉了树套树,强制在线卡掉了 cdq 分治,于是我们只能使用 K - D Tree,这也从一个侧面说明了 K - D Tree 的重要性,毕竟有些出题人会只放 K - D Tree 过。
发现题目中有两个操作,单点加和矩阵求和,因此对于每个点除了维护当前点维护的矩阵外还要维护子树权值和。
我们可以考虑将单点加改成单点插入,点可重,这样就可以直接上 Insert() 的代码不需要任何修改。
对于矩阵求和,考虑从根节点开始,如果有一个点维护的矩阵被完全包含或者完全不包含于查询矩阵中,我们就可以直接返回而不需要再往下搜,否则我们就需要分别统计左右儿子以及自己这个点对答案的贡献。
因为这道题涉及到了插入,所以我们需要注意不平衡时拍扁重构,然后不要写丑,否则你的不重构跑的比重构还快。
GitHub:CodeBase-of-Plozia
Code:
/*
========= Plozia =========
Author:Plozia
Problem:P4148 简单题
Date:2022/1/14
========= Plozia =========
*/
#include <bits/stdc++.h>
typedef long long LL;
const int MAXN = 5e5 + 5;
const double alpha = 0.725;
int a[MAXN], d[MAXN], cntn, n, Root;
struct node { int x, y, val; } s[MAXN];
struct kdtree
{
int ls, rs, Minx, Miny, Maxx, Maxy, lazy, Size; LL val;
#define ls(p) tree[p].ls
#define rs(p) tree[p].rs
#define Minx(p) tree[p].Minx
#define Maxx(p) tree[p].Maxx
#define Miny(p) tree[p].Miny
#define Maxy(p) tree[p].Maxy
#define val(p) tree[p].val
#define lazy(p) tree[p].lazy
#define Size(p) tree[p].Size
}tree[MAXN];
int Read()
{
int sum = 0, fh = 1; char ch = getchar();
for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = sum * 10 + (ch ^ 48);
return sum * fh;
}
int Max(int fir, int sec) { return (fir > sec) ? fir : sec; }
int Min(int fir, int sec) { return (fir < sec) ? fir : sec; }
bool cmp1(const int &fir, const int &sec) { return s[fir].x < s[sec].x; }
bool cmp2(const int &fir, const int &sec) { return s[fir].y < s[sec].y; }
void Make_a(int p)
{
if (!p) return ;
Make_a(ls(p)); a[++cntn] = p; Make_a(rs(p));
}
void Update(int p)
{
val(p) = val(ls(p)) + val(rs(p)) + 1ll * s[p].val;
Size(p) = Size(ls(p)) + Size(rs(p)) + 1;
Minx(p) = Maxx(p) = s[p].x; Miny(p) = Maxy(p) = s[p].y;
if (ls(p))
{
Minx(p) = Min(Minx(p), Minx(ls(p))); Maxx(p) = Max(Maxx(p), Maxx(ls(p)));
Miny(p) = Min(Miny(p), Miny(ls(p))); Maxy(p) = Max(Maxy(p), Maxy(ls(p)));
}
if (rs(p))
{
Minx(p) = Min(Minx(p), Minx(rs(p))); Maxx(p) = Max(Maxx(p), Maxx(rs(p)));
Miny(p) = Min(Miny(p), Miny(rs(p))); Maxy(p) = Max(Maxy(p), Maxy(rs(p)));
}
}
int Build(int l, int r)
{
if (l > r) return 0;
int mid = (l + r) >> 1;
double avex = 0, avey = 0, valx = 0, valy = 0;
for (int i = l; i <= r; ++i) avex += s[a[i]].x, avey += s[a[i]].y;
avex /= (r - l + 1), avey /= (r - l + 1);
for (int i = l; i <= r; ++i) valx += (s[a[i]].x - avex) * (s[a[i]].x - avex), valy += (s[a[i]].y - avey) * (s[a[i]].y - avey);
if (valx > valy) std::nth_element(a + l, a + mid, a + r + 1, cmp1), d[a[mid]] = 1;
else std::nth_element(a + l, a + mid, a + r + 1, cmp2), d[a[mid]] = 2;
ls(a[mid]) = Build(l, mid - 1); rs(a[mid]) = Build(mid + 1, r);
Update(a[mid]); return a[mid];
}
void Check(int &p)
{
if (Size(p) * alpha <= Size(ls(p)) || Size(p) * alpha <= Size(rs(p)))
{
cntn = 0; Make_a(p); p = Build(1, cntn);
}
}
void Insert(int &p, int x)
{
if (!p) { p = x; Update(p); return ; }
if (d[p] == 1)
{
if (s[x].x <= s[p].x) Insert(ls(p), x);
else Insert(rs(p), x);
}
else
{
if (s[x].y <= s[p].y) Insert(ls(p), x);
else Insert(rs(p), x);
}
Update(p); Check(p);
}
int Query(int p, int r1, int c1, int r2, int c2)
{
if (!p || Minx(p) > r2 || Maxx(p) < r1 || Miny(p) > c2 || Maxy(p) < c1) return 0;
if (r1 <= Minx(p) && r2 >= Maxx(p) && c1 <= Miny(p) && c2 >= Maxy(p)) return val(p);
int val = 0;
if (s[p].x >= r1 && s[p].x <= r2 && s[p].y >= c1 && s[p].y <= c2) val += s[p].val;
val += Query(ls(p), r1, c1, r2, c2);
val += Query(rs(p), r1, c1, r2, c2);
return val;
}
int main()
{
Read(); int lastans = 0;
for (; ; )
{
int opt = Read();
if (opt == 3) break ;
if (opt == 1)
{
++n; s[n].x = Read() ^ lastans, s[n].y = Read() ^ lastans, s[n].val = Read() ^ lastans;
Insert(Root, n);
}
else if (opt == 2)
{
int r1 = Read() ^ lastans, c1 = Read() ^ lastans, r2 = Read() ^ lastans, c2 = Read() ^ lastans;
if (r1 > r2) std::swap(r1, r2); if (c1 > c2) std::swap(c1, c2);
printf("%d\n", lastans = Query(Root, r1, c1, r2, c2));
}
}
return 0;
}
4. 总结
K - D Tree 实际上就是用来维护高维空间的一个数据结构,可以做各种替罪羊树能做的事情(因为 K - D Tree 和替罪羊树非常相似),虽然复杂度玄学而且常数大,但不失为一种好的方法。



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 在鹅厂做java开发是什么体验
· 百万级群聊的设计实践
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战
· 永远不要相信用户的输入:从 SQL 注入攻防看输入验证的重要性
· 浏览器原生「磁吸」效果!Anchor Positioning 锚点定位神器解析