数据结构专题-学习笔记：线段树合并
一些 Update
Update 2021/12/16：修改垃圾回收部分的描述，改为更一般的描述空间回收并且加了一些解释说明。
1. 前言
线段树合并，是一种听起来高大上实际上难度并不大的算法，专门用于一些 DS 题目，可以在一定的复杂度内合并两棵线段树，这过程中有时会用启发式合并。
当然，如果你学过任何一种需要合并的数据结构（如 FHQ Treap），那么学习线段树合并将会非常简单。
前置知识：动态开点线段树，树上差分。
2. 详解
先上例题：P4556 [Vani有约会]雨天的尾巴。
题意简述：给出 \(n\) 点连通树，\(q\) 次操作，每次操作对 \(x \to y\) 路径上所有点加入一个大小为 \(z\) 的数，问加完后每个点上哪个大小的数最多，\(n,q \leq 10^5,z \leq 10^5\)。
这道题首先有个最直接的方式就是暴力跑所有路径，然后每个点开一个值域线段树存一下，每个点维护两个值 \(Maxn,ans\) 表示最大数的个数以及这个数，最后每个点查一下就好了，复杂度 \(O(qn \log n)\)，这个做法总应该会的吧qwq，不会好好想想（）
发现这样只有 50pts，于是想想怎么优化，这就需要用到线段树合并了。
首先简要说一下线段树合并的作用：对于两棵动态开点线段树，设这两棵树点数均为 \(x\)，那么线段树合并可以在 \(O(x)\) 的时间内将两棵线段树的信息合并到一棵上。如果两棵树点数不一样就需要看树的结构了，但是可以保证会至多遍历较大树一次。
那么怎么合并呢，就是对两棵树同时暴力 dfs，自底向上更新即可。
听起来确实很暴力呢，说白了就是将两棵树对应的点合到一起，那么他们相关的信息也被合到了一起，只不过实现的时候我们是先合并左右儿子然后再合并这个点，学过别的需要合并的数据结构的应该能很快理解。
画个图解释下：
假设现在我们有两棵线段树，每个点维护区间和（每个点上的数字就是区间和）：
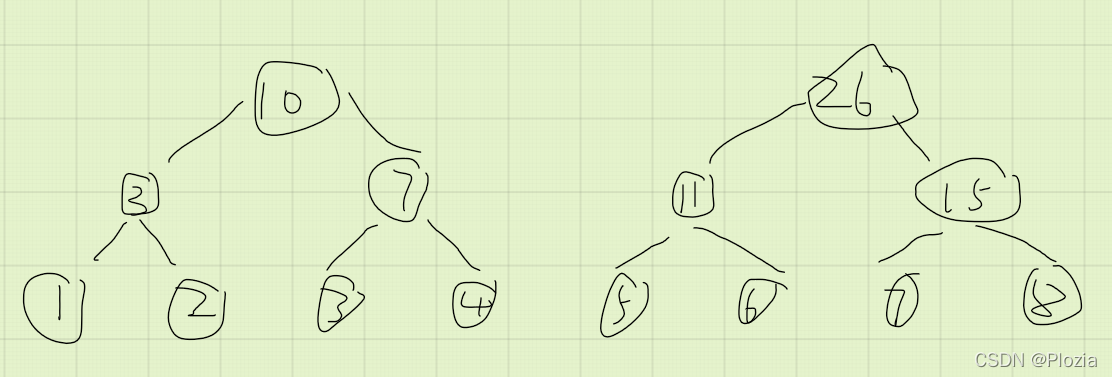
那么现在将这两棵线段树进行合并，结果就是这样的：
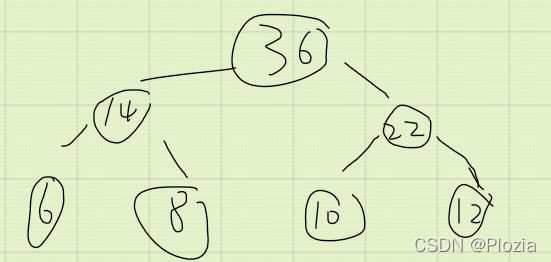
然后实现过程就是暴力！
回到例题，我们发现每次修改都是对路径的修改，于是这里我们可以套上一个树上差分，\(x,y,lca(x,y),fa_{lca(x,y)}\) 这四个点单点修改，然后对这棵树重新 dfs 然后自底向上进行线段树合并即可。
至于为啥复杂度是对的，因为你总共只有 \(4n\) 个节点对吧，因此自底向上合并的时候由于复杂度一般是点数较小树决定的，复杂度不会过 \(O(4n)\)，空间复杂度 \(O(4n \log n)\)。
关于线段树合并的写法就有两种形式了：
先贴一下结构体和 Update 函数：
struct SgT
{
int l, r, Maxn, ans;
#define l(p) tree[p].l
#define r(p) tree[p].r
#define Maxn(p) tree[p].Maxn
#define ans(p) tree[p].ans
}tree[MAXN * 100];
void Update(int p)
{
if (Maxn(l(p)) >= Maxn(r(p))) { Maxn(p) = Maxn(l(p)); ans(p) = ans(l(p)); }
else { Maxn(p) = Maxn(r(p)); ans(p) = ans(r(p)); }
}
一种写法是直接合并，在原树上修改值：
void Merge(int &p1, int p2, int l, int r) // 表示将树 p2 的信息合并到树 p1 上
{
if (!p1 || !p2) { p1 = p1 + p2; return ; }
if (l == r) { Maxn(p1) = Maxn(p1) + Maxn(p2); return ; }
int mid = (l + r) >> 1;
Merge(l(p1), l(p2), l, mid);
Merge(r(p1), r(p2), mid + 1, r);
Update(p1);
}
这种做法的好处是节省了空间，但是坏处是如果你需要询问这个点的相关内容需要在修改之后立刻询问才行，即使是像例题一样做在差分完毕之后统一 dfs 自底向上合并，也需要在这个点合并完之后立刻存下答案，否则就会造成答案错误，因为该做法合并的时候会出现多个树共用一个节点的情况，此时一旦任何一棵树被合并，所有的树答案都会被影响。
该做法只适用于修改完之后即刻询问的做法。
另外一种做法是不修改这个点点值，而是动态开点接着做（边合并边动态开点）：
int Merge(int p1, int p2, int l, int r)
{
if (!p1 || !p2) { p1 = p1 + p2; return p1; }
int p = ++cnt_SgT; // cnt_SgT 是计数器
if (l == r) { Maxn(p) = Maxn(p1) + Maxn(p2); ans(p) = l; return p; }
int mid = (l + r) >> 1;
l(p) = Merge(l(p1), l(p2), l, mid);
r(p) = Merge(r(p1), r(p2), mid + 1, r);
Update(p); return p;
}
这个做法会比较耗空间，但是好处就是你可以边修改边询问，询问修改互不干扰，因为你每次都动态开点了。
当然该做法耗空间是可以避免的，比如你使用一个空间回收的 Trick，这个 Trick 可以将那些再也用不到的点拿回来重复利用，其实相当于指针空间释放再开指针，而且空间回收是不会影响总复杂度的（顶多影响一点常数）。
但是特别的，如果你用了空间回收的话你就需要跟第一个做法一样合并完立刻存下答案了，理由就是空间回收会清空一个点的数据，这对以该节点为根的点的询问会有影响。
不过因为这道题空间复杂度不过 \(O(4n \log n)\)，所以现在不用空间回收也能过。
需要注意的是，如果线段树合并的过程中将一个点的信息存到另一个点上（信息移植，第一种做法）的复杂度与将两者信息提取出来合并到新点上（信息合并，第二种做法）的复杂度相同，那么两种做法都可以用，但是如果不同，则显然信息移植是比信息合并要优的，此时只能采用第二种做法。
比如说有的题，我们只需要单点操作也就是查询叶子结点的值，但是叶子结点的合并需要启发式合并，此时如果采用信息合并做法复杂度就是错的（除非用指针），因为信息合并复杂度是 \(O(Size_1+Size_2)\)，而如果采用信息移植就可以正常启发式合并，复杂度为 \(O(\min\{Size_1,Size_2\})\)。
下面贴模板题代码：
CodeBase：CodeBase-of-Plozia
Code：
/*
========= Plozia =========
Author:Plozia
Problem:P4556 【模板】线段树合并
Date:2021/12/5
========= Plozia =========
*/
#include <bits/stdc++.h>
int Max(int fir, int sec) { return (fir > sec) ? fir : sec; }
int Min(int fir, int sec) { return (fir < sec) ? fir : sec; }
typedef long long LL;
const int MAXN = 1e5 + 5;
int n, q, Head[MAXN], cnt_Edge = 1, Root[MAXN], cnt_SgT, fa[MAXN][21], dep[MAXN];
struct node { int To, Next; } Edge[MAXN << 1];
struct SgT
{
int l, r, Maxn, ans;
#define l(p) tree[p].l
#define r(p) tree[p].r
#define Maxn(p) tree[p].Maxn
#define ans(p) tree[p].ans
}tree[MAXN * 100];
int Read()
{
int sum = 0, fh = 1; char ch = getchar();
for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = sum * 10 + (ch ^ 48);
return sum * fh;
}
void add_Edge(int x, int y) { ++cnt_Edge; Edge[cnt_Edge] = (node){y, Head[x]}; Head[x] = cnt_Edge; }
void Update(int p)
{
if (Maxn(l(p)) >= Maxn(r(p))) { Maxn(p) = Maxn(l(p)); ans(p) = ans(l(p)); }
else { Maxn(p) = Maxn(r(p)); ans(p) = ans(r(p)); }
}
void dfs(int now, int father)
{
dep[now] = dep[father] + 1; fa[now][0] = father;
for (int i = Head[now]; i; i = Edge[i].Next)
{
int u = Edge[i].To;
if (u == father) continue ;
dfs(u, now);
}
}
void init()
{
for (int j = 1; j <= 20; ++j)
for (int i = 0; i <= n; ++i)
fa[i][j] = fa[fa[i][j - 1]][j - 1];
}
int LCA(int x, int y)
{
if (dep[x] < dep[y]) std::swap(x, y);
for (int i = 20; i >= 0; --i)
if (dep[fa[x][i]] >= dep[y]) x = fa[x][i];
if (x == y) return x;
for (int i = 20; i >= 0; --i)
if (fa[x][i] != fa[y][i]) x = fa[x][i], y = fa[y][i];
return fa[x][0];
}
void Insert(int &p, int x, int k, int l, int r)
{
if (!p) p = ++cnt_SgT;
if (l == r && l == x) { Maxn(p) += k; ans(p) = x; return ; }
int mid = (l + r) >> 1;
if (x <= mid) Insert(l(p), x, k, l, mid);
else Insert(r(p), x, k, mid + 1, r);
Update(p);
}
int Merge(int p1, int p2, int l, int r)
{
if (!p1 || !p2) { p1 = p1 + p2; return p1; }
int p = ++cnt_SgT;
if (l == r) { Maxn(p) = Maxn(p1) + Maxn(p2); ans(p) = l; return p; }
int mid = (l + r) >> 1;
l(p) = Merge(l(p1), l(p2), l, mid);
r(p) = Merge(r(p1), r(p2), mid + 1, r);
Update(p); return p;
}
void dfs2(int now, int father)
{
for (int i = Head[now]; i; i = Edge[i].Next)
{
int u = Edge[i].To;
if (u == father) continue ;
dfs2(u, now); Root[now] = Merge(Root[now], Root[u], 1, MAXN - 5);
}
}
int main()
{
n = Read(), q = Read();
for (int i = 1; i < n; ++i)
{
int x = Read(), y = Read();
add_Edge(x, y); add_Edge(y, x);
}
add_Edge(0, 1); add_Edge(1, 0);
dfs(0, 0); init();
for (int i = 1; i <= q; ++i)
{
int x = Read(), y = Read(), z = Read();
int l = LCA(x, y);
Insert(Root[fa[l][0]], z, -1, 1, MAXN - 5);
Insert(Root[l], z, -1, 1, MAXN - 5);
Insert(Root[x], z, 1, 1, MAXN - 5);
Insert(Root[y], z, 1, 1, MAXN - 5);
}
dfs2(0, 0);
for (int i = 1; i <= n; ++i)
{
if (Maxn(Root[i]) == 0) printf("0\n");
else printf("%d\n", ans(Root[i]));
}
return 0;
}
3. 总结
线段树合并就是一种暴力合并算法，结合动态开点线段树完成，但是我们可以通过诸如计算空间复杂度最大值，启发式合并等思路降低复杂度。
