CSP-S 2021 Unofficial 题解
T1 廊桥分配（airport）
这次 T1 带有很大的迷惑性。
其实吧本身这个 T1 不难，以国内区为例子，我们设 \(s_{u}\) 表示当分配给国内区 \(u\) 个廊桥的时候国内区有几架飞机能够停靠，不难发现如果规定 \(s_{u}\) 表示有几架飞机刚好停在第 \(u\) 个廊桥，就可以直接单点修改然后做一遍前缀和。
由于飞机停靠遵循先来后到原则，因此实际上求出 \(s_{u}\) 数组是可以用两个优先队列解决的，复杂度 \(O(n \log n)\)。
对国内区和国际区分别做一次，得到 \(s1,s2\) 两个数组之后，答案就是 \(\max_{i=0}^{n}(s1_i+s2_{n-i})\)。
这个做法倒是挺简单的，就是一个贪心思路，但问题是考场上给的两个小样例很具有迷惑性，让人以为如果设 \(f(x)=s1_x+s2_{n-x}\)，这个 \(f(x)\) 是满足单峰性的，然后很多人就写了个三分于是愉快的挂掉了（）
实际上考场上的大样例输出来看一眼就知道 \(f(x)\) 并不满足单峰性，然后就知道三分是假的了。
当然那个大样例的图画出来大概是这样的：
也就是说实际上大样例面对部分三分是能过的，还是相对比较水，当然至少有些人的三分被卡了。
Update：貌似三分的时候 \(r-l>50\) 之后转暴力就能场切……
T2 括号序列（bracket）
谁用两个数组前缀和优化啊，不是暴力枚举若干种情况更好算更好写（
翻了下洛谷题解，发现有一个暴力枚举 6 种可能状态的，这个做法看起来不错也和只用两个数组持平，因为你只用两个数组照样有 5,6 个转移方程，但是这个方法每个状态只需要一个转移方程所以本质没变（
下称超级括号序列为括号序列。
首先最基础的，设 \(f_{l,r,0}\) 表示区间 \([l,r]\) 内全为 * 的方案数，\(f_{l,r,1}\) 表示区间 \([l,r]\) 内表示为 (AAAA),(SASASA),(ASASAS),(S) 的方案数（A 为合法括号序列，S 为全 * 序列（有时长度可为 0，会说明），下同），其实就是 \(l,r\) 两个位置括号匹配，\(f_{l,r,5}\) 表示区间内为 ASASASA 的方案数，S 长度可以为 0，A 也可以只有一个（即 1 被 5 包含）。
其中 \(f_{l,r,0}\) 内 (S) 情况下 S 长度可以为 0，\(f_{l,r,5}\) 中 S 长度也可以为 0，据此可以发现初值 \(f_{i+1,i,0}=1\)。
接下来考虑要维护什么，注意到 \(f_{l,r,1}\) 中转移有 SASASA,ASASAS，因此设 \(f_{l,r,2}\) 表示 ASASAS 形式，\(f_{l,r,3}\) 表示 SASASA 形式，这样 \(f_{l,r,1}\) 转移就好了。
至于 \(f_{l,r,5}\)，为了避免算重，考虑枚举串中需要的第一个 A，这样剩下的就是形如 SASASA 的，用 \(f_{l,r,3}\) 即可。
考虑 \(f_{l,r,2},f_{l,r,3}\) 的转移，注意到枚举掉第一个 S/A 后剩下的都是形如 SASASAS 的，因此设 \(f_{l,r,4}\) 表示 SASASAS 的情形，而这个转移在枚举了第一个 S 之后变成了 ASASAS，就是 \(f_{l,r,2}\)。
然而我们需要明确一下这里面 S 是否能为空（显然 A 是可以相邻的但 S 不能相邻且部分情况不能为空），因此 6 个状态的相对严谨定义如下：
- \(f_{l,r,0}\)：
S，其中S不可为空。 - \(f_{l,r,1}\)：
(A),(SASA),(ASAS),(S)，其中(A)中A可为空（这里的A可以是广义上的括号序列，也就是 \(f_{l,r,5}\)，但是别的均不可以），(S)中S不可为空；(SASA),(ASAS)中两端的S和A不可为空，其余可为空。 - \(f_{l,r,2}\)：
ASAS，其中两端的S均不可为空，其余S可为空。 - \(f_{l,r,3}\)：
SASA，其中两端的S均不可为空，其余S可为空。 - \(f_{l,r,4}\)：
SASAS，其中两端的S不可为空，其余S可为空，特别的，本情况包含 \(f_{l,r,0}\)（即单独有一个S）。 - \(f_{l,r,5}\)：
ASASASA，S可为空，特别的，本情况包含 \(f_{l,r,1}\)（即单独有一个A）。
注意 \(f_{l,r,4}\) 和 \(f_{l,r,5}\) 包含单个 S/A 的情况是方便转移，实际上你也可以强制规定必须至少有 SAS/AA(ASA) 等子串，但是那样子转移写起来烦一点。
接下来考虑转移（\(l<r,len=r-l+1\)）：
- \(f_{l,r,0}\)：特判一下就好了，注意判掉 \(len>k\) 的情况因为这样非法。
- \(f_{l,r,1}\)：如果 \(l,r\) 两个位置能构成一对括号，则有转移 \(f_{l,r,1}=f_{l+1,r-1,0}+f_{l,r,5}+f_{l,r,3}+f_{l,r,2}\)，否则不能转移。
- \(f_{l,r,2}\)：考虑枚举第一个
A，由于中间S可为空那么可以是ASAS也可以是SASAS，则 \(f_{l,r,2}=\sum_{k=l}^{r-1}f_{l,k,1}\times (f_{k+1,r,2}+f_{k+1,r,4})\)。后面的类似，都是枚举第一个S/A然后考虑第二个位置是不是S即可。 - \(f_{l,r,3}=\sum_{k=l}^{r-1}f_{l,k,0}\times f_{k+1,r,5}\)。
- \(f_{l,r,4}=\sum_{k=l}^{r-1}f_{l,k,0}\times f_{k+1,r,2}\)。
- \(f_{l,r,5}=\sum_{k=l}^{r-1}f_{l,k,1}\times(f_{k+1,r,3}+f_{k+1,r,5})\)。
- 所有 \(f_{l,r,p}\) 算完后，\(f_{l,r,5}\leftarrow f_{l,r,1}+f_{l,r,5},f_{l,r,4}\leftarrow f_{l,r,0}+f_{l,r,4}\)。
最后答案 \(f_{1,n,5}\)。
T3 回文（palin）
这道题我考场上的时候敲了个 \(O(2^n)\)（不是 \(O(2^{2n})\)） 的代码，然后成功搞到 40pts。
进入正题。
我们设 \(Match_i\) 表示互相相等的两个数，另外那个数的位置，也就是说如果 \(a_i=a_j\)，那么 \(Match_i=j,Match_j=i\)。
然后我们就可以得到一个奇怪的性质：设每次取出 \(a_i\) 之后我们在 \(Match_i\) 位置上打个标记，那么除第一个数之外，每次取出的数 \(a_j\) 其 \(Match_j\) 位置左右两边有且仅有一个位置是有标记的。
证明的话其实也比较简单：
我们发现箭头指的那个点左右两边都被打标记了，这个数所匹配的另一个数比左右两个数都要迟一点取出，由于取出的数列是个回文串，那么这个打箭头的数必须要先被取出，可是这样的话左右两边就有一个数要被取出了，这样就打破了回文串的性质。
啥你说两边都没有标记可不可以？问题是想想都知道不可能啊，只有第一个数会出现这种情况除非你写挂了（
然后我们根据上述性质贪心的从左边选，找到解就输出，没了。
这个复杂度是 \(O(T\sum n)\) 的，但是我不会证qwq
T4 交通规划（traffic）
这题只有紫我是不认同的，我认为应该是黑（不过最开始是黑后来降紫的），主要是这题没学过网络流基本不会做法虽然学过也不会，以及为什么这题洛谷上卡常啊？
下面默认所有附加点颜色不会均相同。
首先可以注意到题目要求将每个点染色使得所有同色附加点与异色附加点隔开，也就是要求分成若干个黑白连通块，且黑白连通块的交界边的边权最小，然后有一个显然的结论就是尽可能使连通块个数少，显然。
然后就有一个网络流的做法：建立超源超汇，其中超源连向所有白色点，所有黑色点连向超汇（这里都是单向边，注意如果只有一个颜色直接输出 0），然后原题转化为求最小割，跑一遍最大流即可，使用朴素的 dinic 可以做到 [60, 65]pts，如果网络流大力卡常加优化可以过，但是显然你赛场上写不出来加了无数优化的 HLPP（
部分分有很多 \(k=2\)，实际上也是对做法提示最大的一部分。考虑将 \(k=2\) 和网络流结合起来（红色是最小割）（图是手绘，略丑见谅）：
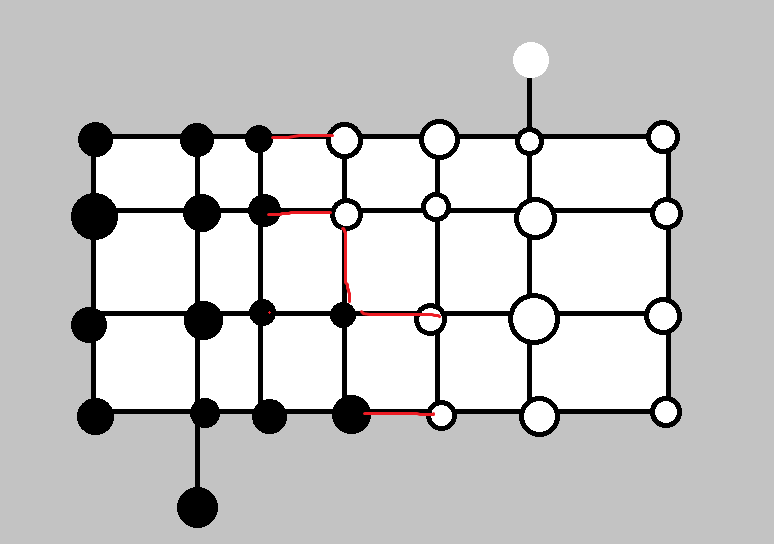
然后看了看，这似乎能用一条线画出来？
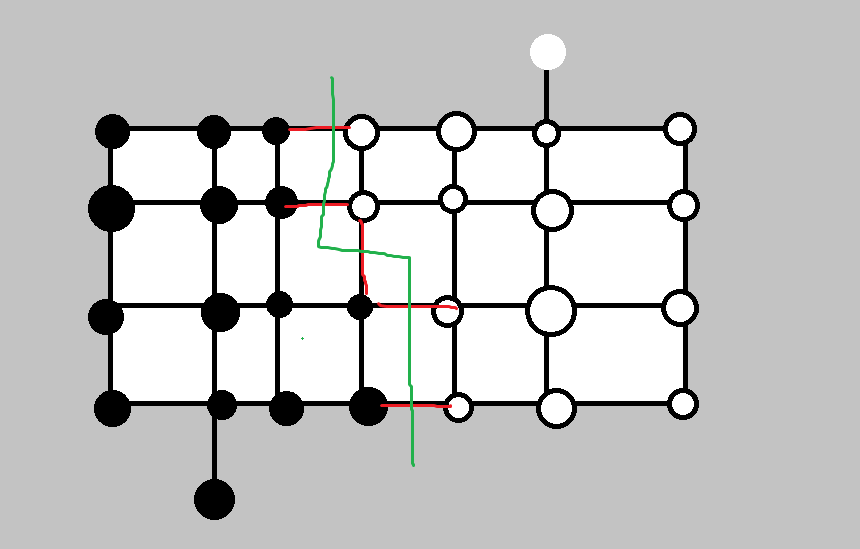
想想也合理，毕竟我们是要将这些附加点分成若干个连通块，连通块的分界线自然也可以用一条线画出来。
由于网络流不可行所以需要另想办法，注意到这条线一定会经过很多的边然后经过网格，于是可以考虑将这些网格作为点，四连通相邻网格间边权就是中间这条隔断的边，转化后的图如下（附加点还没动）：
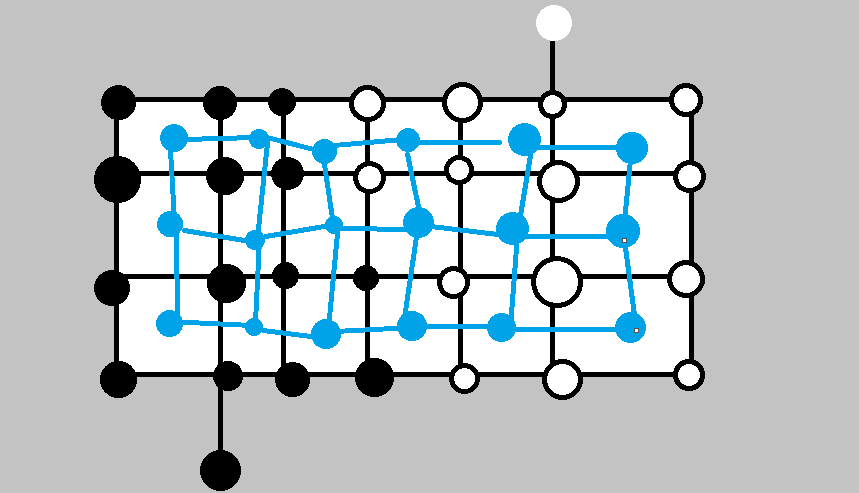
此时你发现，最小割就转化成了若干条连续的边组合，也就是最短路。但是没有起点终点？
附加点就是起点终点，注意到两个附加点颜色不同，将外面的灰色部分本质上分隔成了两个连通块，这两个连通块就是起点终点，而连边就是通过最外围的一圈连进去，如下：
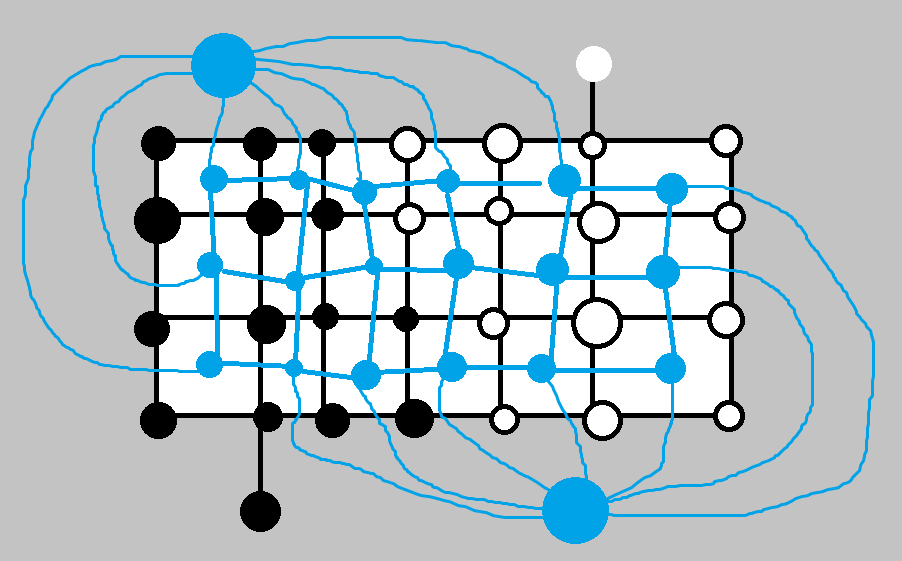
至此，问题转化为求起点和终点的最短路。
接下来考虑 \(k\ne2\) 的做法，其实还是可以弄成很多很多的起点和终点：
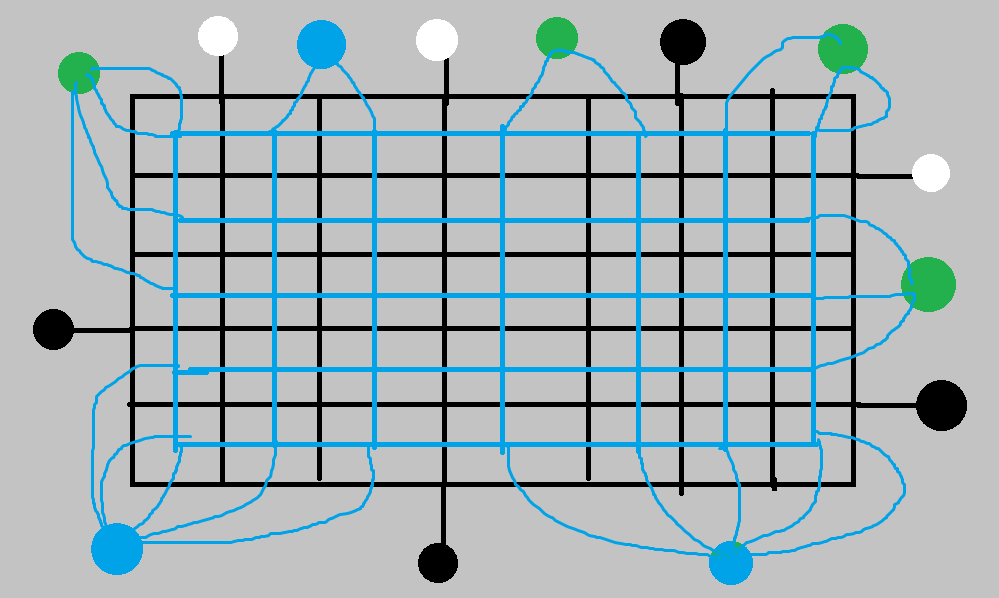
注意到上式有部分绿色点和蓝色点，绿色点隔壁两个附加点异色，白色点隔壁两个附加点同色，其实就是说所有的绿色点作为起终点需要两两配对，而蓝色点完全可以并到隔壁的两个附加点中，这样也能使连通块个数最小。
这样，题目就变成了有若干个点，将这些点两两配对使得每一对的最短路之和最小，下面为了方便将所有起终点顺时针排序。
然后有两个结论：起终点配对方案数就是相同长度的合法普通括号序列的方案数（不是超级括号序列），所有起终点路径无交。
这两个结论证明很麻烦，感性理解就是钦定起终点配对之后相邻的显然能够靠的更近因此有括号序列，然后无交就是说有交了可以将中间部分消掉，严谨证明算了，分类讨论太多很困难。
接下来考虑如何求解答案，注意到答案形式一定是括号序列之后就可以设计 dp（要断环成链）：设 \(f_{i,j}\) 表示第 \(i\) 个点到第 \(j\) 个点的答案，根据括号序列转移式可得 \(f_{i,j}=\min\{f_{i+1,j-1}+d_{i,j},\min_{k=i}^{j-1}\{f_{i,k}+f_{k+1,j}\}\}\)，其中 \(d_{i,j}\) 表示 \(i\) 点到 \(j\) 点的关键点。
这样就做完了，复杂度？建图部分 \(O(nm+k)\)，跑最短路暴力跑 \(O(nmk)\)，dp 求解 \(O(k^3)\)，显然可过。
但是有几个点需要注意：
- 转化图的时候每个点编号不要搞错。
- 这题洛谷上有点卡常，所以如果发现自己卡不进去记得只在 dp 的时候开 long long 别的时候全开 int，如果还进不去可能还需要哪个地方再卡卡常或者夜深的时候交。
- 数组开大。
还有很多实现上的细节不提了，谁写谁知道（
总结
2022/11/2 来写的总结，现在过来看发现 T1,T3 两个题还是比较简单的，然后 T2 的 dp 涉及如果用两个数组前缀和优化写起来很烦，但是如果用 6 个状态就比较容易算重而且状态设计相对难想一点，不过综合考虑建议赛时用第一个做法（你也基本上想不到第二个做法），但是赛后补题的时候可以使用第二个做法，至于 T4 网络流推正解这一步差评（没学过很难推），卡常差评，但是图的转化这一步是很妙的。
