图论专题-学习笔记:2 - SAT 问题
一些 update
update 2021/11/12:修正了文章中的一些语言。
1. 前言
本篇文章将会对 2 - SAT 问题做一个讲解。
前置知识:强连通分量/缩点。
2. 详解
首先我们需要知道 2 - SAT 是什么。
实际上 2 - SAT 是 k - SAT 的一种特殊情况。
k - SAT 问题的一般描述就是有一些物品,每个物品均有 \(k\) 个状态,给出一些限制条件,诸如 A 为 a 状态则 B 为 b 状态之类的,问有无可行解,有时还会让你求解。
目前 k - SAT 问题(\(k > 2\))已经被证明无多项式解法,只能暴力求解,但是 2 - SAT 因为其优良的性质使得当我们只需要任意一组解或者是判有无解的时候,可以采用 \(O(n + m)\) 算法解决。
2 - SAT 一般描述如下:
现给出 \(n\) 个布尔类型的值,可真可假,有 \(m\) 种限制条件,限制条件是如下 3 种情况之一:
- 若 \(A = p\),则 \(B = q\)。
- \(A = p\) 与 \(B = q\) 至少有一个成立。
- A 必须为 \(p\)。
剩余别的所有情况都可以转化为上述三种情况。
现给出这些限制条件,问你有没有一组取值,使得这组取值能够满足所有限制条件,如果有还需要求出一组可行解。
解决 2 - SAT 问题的方案一般是建图。
对于每一个变量 \(x\) 我们建两个点 \(x_0,x_1\),分别表示变量 \(x\) 取 0 或者取 1。
- 若 \(A = p\),则 \(B = q\)。
为了方便,只讨论若 \(A = 1\),则 \(B = 1\),其余情况可以类推。
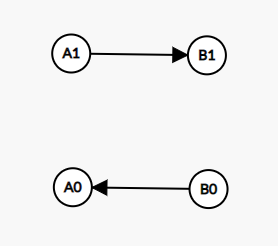
考虑连边 \(A_1 \to B_1,B_0 \to A_0\),这么连边的意义是如果 \(A = 1\),那么根据连边可以推出 \(B = 1\),如果 \(B = 0\),那么根据连边可以推出 \(A = 0\)。
注意 \(B_0 \to A_0\) 正确性是因为原命题的逆否命题正确。
- \(A = p\) 与 \(B = q\) 至少有一个成立。
为了方便,只讨论 \(A = 1\) 与 \(B = 1\) 至少有一个成立,其余情况可以类推。
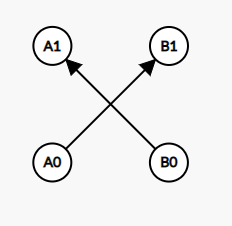
考虑连边 \(A_0 \to B_1,B_0 \to A_1\),意义是如果 \(A = 0\) 则 \(B = 1\) 必然成立,同理 \(B = 0\) 则 \(A = 1\) 必然成立。
- A 必须为 \(p\)。
为了方便,只讨论 \(A = 1\) 的情况,其余情况可以类推。
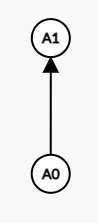
对于这种情况,直接连边 \(A_0 \to A_1\),意义是如果 \(A = 0\),根据连边可以发现 \(A = 1\),这意味着 \(A \ne 0\),只能是 \(A = 1\),该连边可以控制 \(A \ne 0\)。
这么操作之后,我们得到了一张有向图,其中的有向边表示推出关系。
那么接下来如何判断有无解呢?
采用强连通分量算法。
假设说某变量 \(x\),其两个点 \(x_0,x_1\) 处于同一个强连通分量中,这说明从 \(x = 0\) 出发能够推出 \(x = 1\),从 \(x = 1\) 出发能够推出 \(x = 0\),因此 \(x \ne 0,x \ne 1\),这样就无解了。
那么如何求出一组可行解呢?
首先对这一张图缩点,然后我们就得到了一张 DAG。
如果 \(x_0\) 处于强连通分量 \(A\) 中,\(x_1\) 处于强连通分量 \(B\) 中,且 \(A\) 的拓扑序小于 \(B\),那么有两种可能:
- \(x_0,x_1\) 互不干扰。
- \(x_0\) 能够推出 \(x_1\)。
发现无论哪种情况选择 \(x_1\) 都是正确的,因此对于变量 \(x\) 而言,\(x_0,x_1\) 哪个拓扑序大选哪个能够保证选出来的解是正确的。
所以我们需要对建出来的图缩点,然后跑拓扑排序,求出拓扑序,然后求解……
吗?
不需要!在求强连通分量的时候我们已经得到拓扑序了。
若采用 Kosaraju 算法(两遍 dfs):
求强连通分量的时候我们会得到一个 Color[] 数组表示其属于的强连通分量的编号,而根据 Color[] 数组可以直接推出两个强连通分量的拓扑序大小:
- 对于缩点之后的图上的两个点 \(i,j\),如果 \(Color_i < Color_j\),则 \(i\) 一定能够走到 \(j\)。换言之,求出这张图的拓扑序后 \(i\) 在 \(j\) 前面。
上述结论的证明过程我在我的文章图论专题-学习笔记:强连通分量中证明过,此处不再证明,想了解的读者可以进入我的文章了解。
实质上 Color[] 就是新图的拓扑序(之一)。
若采用 Tarjan 算法:
采用 Tarjan 算法需要注意的一点就是求出的 scc[] 数组是反过来的,也就是说 scc[] 越大其拓扑序越小,这点跟 Kosaraju 算法是不一样的,也比较容易出错。
证明的话实际上是因为 Tarjan 求强连通分量的时候我们是倒着标记强连通分量的,因此拓扑序最小的强连通分量其标号是最大的。
我更推荐 Kosaraju 算法~
洛谷模板题:P4782 【模板】2-SAT 问题。
洛谷的模板题只有情况 2。
Code:GitHub CodeBase-of-Plozia P4782 【模板】2-SAT 问题.cpp
3. 总结
2 - SAT 问题的一般解法是根据逻辑关系进行拆点连边,然后求强连通分量判断有无解以及求出一组解。


