数学/数论专题-专项训练:线性基#2
0. 一些 update
update on 2021/7/17:增添了 P4151 [WC2011]最大XOR和路径 的一些说明。
1. 前言
本篇博文是作者学习线性基时候的一些专项训练,难度比数学/数论专题-专项训练:线性基#1稍微大了一点。
因为作者是个 OIer,本文只讨论 OI 中常见的线性基。
阅读本文前请先确保学过线性基。
2. 练习题
题单:
P4301 [CQOI2013] 新Nim游戏
做这道题需要知道一个前置知识:传统 Nim 游戏的先手必败条件为 \(\bigoplus_{i=1}^{n}a_i=0\)。
因此先手需要想个办法使得不管后手怎么拿,都组合不出 0。
而线性基具有如下两个性质:
- 线性基内的数不能异或出 0。
- 对于一个序列 \(d\) 而言,其线性基数的个数是固定的,不会因为插入数的顺序而改变。
因此我们可以考虑求一下原序列的线性基。
在求线性基的过程中我们会得到一些数插入失败,而这些数就是要被拿走的数,拿走之后剩下的数就不能异或出 0 了(因为线性基内的数不能异或出 0 了)。
题中要求取走火柴数尽量小,那么我们只需要将 \(a_i\) 从大到小排序就可以了。
Code:GitHub CodeBase-of-Plozia P4301 [CQOI2013] 新Nim游戏.cpp
P4151 [WC2011]最大XOR和路径
对于一条 \(1 \to n\) 的路径,我们可以拆成两部分:一些环 + 一条链。
先不考虑链,求一下环能异或出的最大值。
我们可以搜索出所有的环,然后将这些环上的异或权值全部丢到线性基里面,那么对于求出来的线性基我们求个最大值就好了。
那么这一条链要怎么选呢?实际上这一条链可以随便选。
简单证明一下:
假设路径 \(B\) 比路径 \(A\) 更优,由于 \(A,B\) 共同构成了一个环,那么在异或线性基的时候 \(A\) 会异或上这个环,这样路径就变成了 \(B\)。
因此选哪条链是没差别的。
Code:GitHub CodeBase-of-Plozia P4151 [WC2011]最大XOR和路径.cpp
增加一个说明:
考虑一下下面这张图:
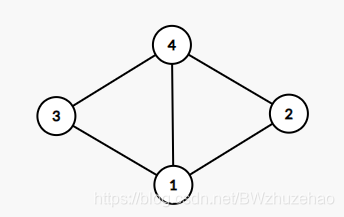
考虑两种可能的 DFS 树:
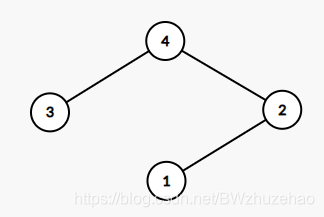
此种情况将会出现环 \(\{1,2,4,3\},\{1,2,4\}\)。
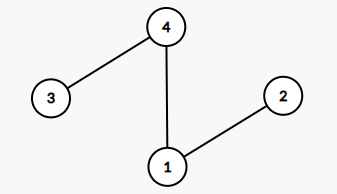
此种情况会出现 \(\{3,4,1\},\{4,1,2\}\)。
我们发现两种情况出现的环并不相同,那么为什么答案是对的呢?
实际上第一种情况得到环 \(\{1,3,4\}\) 的方法就是先将两个环写成边集的形式:\(\{(3,4),(4,2),(2,1),(1,3)\},\{(1,2),(2,4),(4,1)\}\)。
对这两个集合进行异或,可以直接得到 \(\{(3,4),(4,1),(1,3)\}\),也就是环 \(\{1,3,4\}\)。
因此我们可以说明不同的 DFS 树对于得到的最后结果实际上是一样的,可以用大环异或小环得到另外一个小环。
P5556 圣剑护符
首先我们需要转化一下查询操作的题意:查询两个不同子集其异或结果相同等价于查询是否有一个非空子集使得其异或结果为 0。
那么转化题意之后两个操作就变成了树上路径异或,树上路径查询。
发现查询操作可以使用线性基来维护。
哈?你跟我说这么多点都用线性基?
因此这道题我们需要一点类似于根号分治的思想。
发现值域为 \([0,2^{30})\),因此线性基内数的个数至多只有 30 个,对于那些路径长度大于 30 的直接输出 YES。
对于小于 30 的路径呢?由于数的数量很少,直接插入线性基不就好了。
因此现在我们整理一下查询做法:根据路径长度分类,大于 30 直接输出 YES,否则就直接暴力线性基查询。
发现我们需要知道路径长度以及 LCA,这玩意貌似求个深度然后倍增就可以了。
但是因为存在修改操作,因此我们采用树链剖分。
对于修改操作,树剖之后我们直接维护一棵线段树区间修改即可,由于异或满足交换律和结合律因此正确性是对的。
查询操作上面已经讲过了,但是因为我们已经树剖了因此求 LCA 和路径长度直接树剖查询即可。
然后这道题就做完了,注意一下线性基的清 0。
Code:GitHub CodeBase-of-Plozia P5556 圣剑护符.cpp
3. 总结
线性基实际上只是一种工具(从后面两题可以清晰的看出来),对于一些异或结果为 0 或者是异或的最大最小值问题线性基有很好的效果。
但是虽然线性基这么好用,也需要注意不是时时刻刻异或问题都是线性基可以解决的。
- 不要忘记拆位处理这个技巧。
- 如果是最大/最小值问题,有时会采用线性基。
- 对于一些推式子的问题,不要忘记这个式子:\(a \oplus b=a \mid b - a \& b\)。
- 对于一些其他问题,就是普通的二进制问题,不用想多。


