P3640 [APIO2013]出题人 题解

一道神仙图论题，很考验各位对最短路以及染色问题的理解。

首先说明 1 点，实质上神秘问题就是经典的染色问题。

---

这里首先简要分析一下给出的几个代码的特色：

• FloydWarshall：稳定的 $O(V^3)$ 运行。下称 Floyd。
• OptimizedBellmanFord：加了优化的 Bellman-Ford，但是只要在每一轮松弛的时候有一个点的 $dis$ 被改变了就会被彻底卡成 $O(V^2E)$，于是负环可以派上用场。下称 Bellman-Ford/BF。
• ModifiedDijkstra：也有人说这是堆优化的 SPFA，这玩意在正权图上表现良好，但是只要我们构造一些奇怪的负权边就被卡掉了，更具体的分析见后文。下称 Dijkstra/dij。
• Gamble1：永远不会 TLE。
• Gamble2：永远会 TLE。
• RecursiveBacktracking：暴力染色的代码，这玩意及其容易卡。下称 RB。

---

Subtask 1：放 Dijkstra，卡掉 Floyd，$T=107$。

Subtask 3：放 Bellman-Ford，卡掉 Floyd，$T=105$。

因为计数器大于 1000000 时就会 TLE，因此我们只需要构建一组有 101 个点，但是没有任何边的图就可以了。

询问只需要询问 1 组，随便哪两个点都行。

$T=1+101+1+2=105$，能够通过这两个点。

---

Subtask 2：放 Floyd，卡掉 Bellman-Ford，$T=2222$。

Subtask 5：放 Dijkstra，卡掉 Bellmam-Ford，$T=1016$。

这两组数据需要卡掉 BF。

但是前面已经分析过，只需要来一个简单的负环，然后边数尽量大就好。

对于 Subtask 2：点数 $V=100$，然后搞一个负环，边数尽量大即可。

对于 Subtask 5：由于 dij 在负权图上容易被卡，因此我们需要一条 $0->1$ 的单向边，然后 $2,3,4$ 构成负环，剩下的所有点随便连边，边数尽量大就好。注意 $0,1$ 这两个点必须是单独构成一个连通块。

---

Subtask 4：放 Floyd，卡掉 Dijkstra，$T=157$。

Subtask 6：放 Bellman-Ford，卡掉 Dijkstra，$T=143$。

本题最难的两个点，需要好好研究一下题目中的 dij 代码。

P.S. 如果你是非 C++ 党或者懒得研究代码，请直接跳到两份代码后面的分析。

首先一般的 Dijkstra 代码是这样的：（我写的一份）

void dijkstra()
{
    memset(dis, 0x3f, sizeof(dis));
    memset(book, 0, sizeof(book));
    priority_queue <pri> q; q.push((pri){1, 0}); dis[1] = 0;
    while (!q.empty())
    {
        pri x = q.top(); q.pop();
        if (book[x.now]) continue ;
        book[x.now] = 1;
        for (int i = Head[x.now]; i; i = Edge[i].Next)
        {
            int u = Edge[i].to;
            if (dis[u] > dis[x.now] + Edge[i].val)
            {
                dis[u] = dis[x.now] + Edge[i].val;
                if (!book[u]) q.push((pri){u, dis[u]});
            }
        }
    }
}

题目给的是这样的：

while (Q--) {
    scanf("%d %d", &s, &t);

    vector<int> dist(V, INF);
    dist[s] = 0;
    priority_queue< IntPair, vector<IntPair>, greater<IntPair> > pq;
    pq.push(IntPair(0, s));
    while (!pq.empty()) {
      counter++;
      if (counter > 1000000) {
        printf("TLE because iteration counter > 1000000\n");
        return 1;
      }

      IntPair front = pq.top(); pq.pop();
      d = front.first; u = front.second;
      if (d == dist[u]) {
        for (j = 0; j < (int)AdjList[u].size(); j++) {
          IntPair v = AdjList[u][j];
          if (dist[u] + v.second < dist[v.first]) {
            dist[v.first] = dist[u] + v.second;
            pq.push(IntPair(dist[v.first], v.first));
          }
        }
      }
    }

    printf("%d\n", dist[t]);
  }

大致特色是这样的：

• 题目给的代码是对于每一组询问都做一遍 Dijkstra。于是我们只需要构造 10 组相同询问，每组询问运行次数超过 100000 即可。
• 对比两份代码，会发现题目给的代码并没有 $book$ 数组。这将会导致答案正确，但是我们可以构造一些奇怪的东西卡掉它。
• 其实如果你对 SPFA 这个已死的算法足够精通的话，你还会发现实际上这个代码是优先队列优化的 SPFA（SLF 优化 SPFA）。而一个常识就是 SLF 优化 SPFA 是可以被卡成指数级别的，因此我们也可以尝试着将其卡成指数级别。

那么怎么卡呢？看下图：

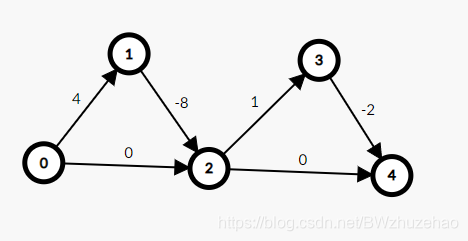
我们从 0 开始找，走 $0 \to 2 \to 4$，走不了了，返回。

然后 $2 \to 3 \to 4$，发现能够更新最短路。

在更新完 $2,3,4$ 之后算法回退到 1，然后走 $0 \to 1 \to 2$，会发现能够更新 $2$ 的最短路。

然后又重复上面的过程，傻傻的 Dijkstra 就被我们卡掉了。

总结一下就是：

• 考虑构建一个形如上面的三元环 $V,V+1,V+2$，$V$ 向 $V+2$ 连一条边权为 0 的边，向 $V+1$ 连一条边权为 $dis$（$dis$ 很大），然后 $V+1$ 向 $V+2$ 连一条边权为 $-dis \times 2$ 的边。
• 然后构建 $V+3,V+4,V+5$，不过此时 $dis$ 需要除以 2。

这样做的原理就是在一个三元环中，$V$ 将会走到 $V+2$ 两次：$V \to V+2$，$V \to V+1 \to V+2$，而且只要 $V$ 被走到就会重复上述过程。

当然你也可以不这么构建，反正只要原理相同就可以了。

于是我们只要构建足够多的三元环，就可以顺利的将 Dijkstra 卡成指数级别。

Bellman-Ford 呢？

反正这玩意没有负环，BF 不是随便跑qwq

对于 Floyd，你根本没法构造点数大于 100 的图（$T$ 很小），而且你也没必要构造，只需要卡掉 Dijkstra 就好了~

这两个 Subtask 有两个需要注意的地方：

• 千万注意连边顺序，一定是先连 $V \to V+2$，再连 $V \to V+1 \to V+2$，否则 Dijkstra 会一次得出正确答案。
• 由于这两个 Subtask 的 $T$ 都非常小，因此一定要注意你一共输出了多少个整数，需要计算清楚。

---

Subtask 7：卡掉 RecursiveBacktracking。

Subtask 8：放 RecursiveBacktracking。

暴力染色的代码太好卡了，只要构造一个近似完全图就可以将这玩意卡掉，随机都行。

前提：不是非酋。

放 RB 过也很简单，因为染色问题的暴力代码在二分图上表现良好，于是我们只需要构造一个二分图即可。

但是这两个 Subtask 有最小限制 $V \geq 71，E \geq 1501$。

计算一下：$2 + 1501 \times 2=3004$，要求只能有 3004 个整数。

看样子这两组点是要到极限了。

然而暴力染色代码复杂度在二分图上跟点数没有太大关系，而对于 Subtask 7 反正你是要卡掉它。

于是这两个点 $V=100$（对于 Subtask 8 可以更大），然后 $E=1501$。

Subtask 7 随便构造近似的完全图，Subtask 8 构造二分图即可。

---

Summary：

这道题让我们见识到了毒瘤出题人卡你最短路的若干种方法各种最短路算法（Floyd，优化 Bellman-Ford，SLF 优化 SPFA）的优缺点，是一道非常好的图论题，可以加深对最短路的了解与掌握。