P3623 [APIO2008]免费道路 题解
最小生成树好题。
下面规定鹅卵石路长度为 1,水泥路长度为 0,则题中要求的是一棵边权为 的生成树。
这道题一开始的时候我会认为边权为 1 的边可以随便加,毕竟根据样例来看,删这一条换另一条并没有什么问题。
于是就有一种做法是先选好 条 1 边,然后剩下的 0 边随意加。
然而根据下面这张图,你就会发现上述做法有问题:
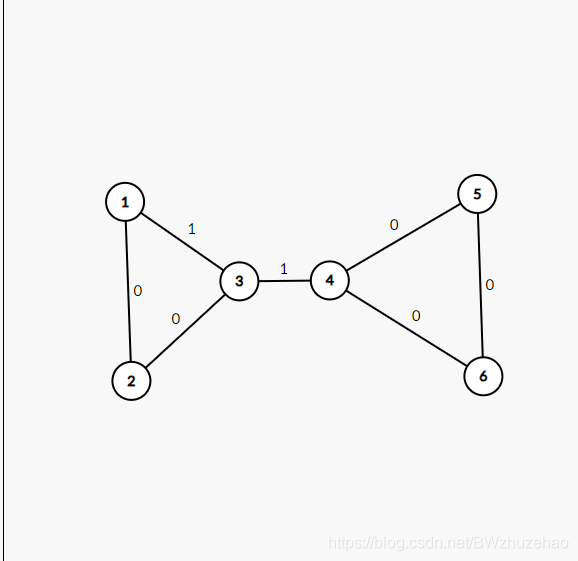
如果此时 ,而你又挑选了 的话……
此时图根本不连通!
因此,有一些边是一定要加的。
那么怎么知道哪些边一定要加呢?
考虑对图做一遍最小生成树,记录一下加入到最小生成树的 1 边数量,这些 1 边就是一定要加的,因为如果删了这些边就不合法了。
然后呢?先加入这些必须加的 1 边,然后在剩下的所有 1 边中加边直到加满,这些边是可以随便选的。最后拿 0 边补齐即可。
无解情况:
- 必须加的 1 边大于 。
- 总共的 1 边不足 。
代码:
/*
========= Plozia =========
Author:Plozia
Problem:P3623 [APIO2008]免费道路
Date:2021/4/22
========= Plozia =========
*/
#include <bits/stdc++.h>
typedef long long LL;
const int MAXN = 20000 + 10, MAXM = 100000 + 10;
int n, m, k;
struct node { int x, y, z; } a[MAXM];
struct Union
{
int fa[MAXN];
void init() { for (int i = 1; i <= n; ++i) fa[i] = i; }
int gf(int x) { return (fa[x] == x) ? x : fa[x] = gf(fa[x]); }
void hb(int x, int y) { if (gf(x) != gf(y)) fa[fa[x]] = fa[y]; }
}u;
int read()
{
int sum = 0, fh = 1; char ch = getchar();
for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = (sum << 3) + (sum << 1) + (ch ^ 48);
return sum * fh;
}
bool cmp1(const node &fir, const node &sec) { return fir.z < sec.z; }
bool cmp2(const node &fir, const node &sec) { return fir.z > sec.z; }
int main()
{
n = read(), m = read(), k = read();
for (int i = 1; i <= m; ++i) a[i].x = read(), a[i].y = read(), a[i].z = read() ^ 1;
std::sort(a + 1, a + m + 1, cmp1);
u.init(); int tmp, sum;
tmp = 0, sum = n;
for (int i = 1; i <= m; ++i)
{
if (u.gf(a[i].x) != u.gf(a[i].y))
{
u.hb(a[i].x, a[i].y);
if (a[i].z == 1) a[i].z = -1, ++tmp;
--sum; if (sum == 1) break ;
}
}
if (tmp > k) { printf("no solution\n"); return 0; }
if (sum != 1) { printf ("no solution\n"); return 0; }
std::sort(a + 1, a + m + 1, cmp2);
u.init(); sum = n;
for (int i = 1; i <= m; ++i)
if (a[i].z == -1) { --sum; u.hb(a[i].x, a[i].y); }
for (int i = 1; i <= m; ++i)
{
if (sum == 1) break ;
if (a[i].z == -1) continue ;
if (tmp == k && a[i].z == 1) continue ;
if (u.gf(a[i].x) != u.gf(a[i].y))
{
u.hb(a[i].x, a[i].y);
if (a[i].z == 1) ++tmp, a[i].z = -1;
if (a[i].z == 0) a[i].z = -2;
--sum; if (sum == 1) break ;
}
}
if (tmp != k) { printf("no solution\n"); return 0; }
for (int i = 1; i <= m; ++i)
{
if (a[i].z == -2) printf("%d %d 1\n", a[i].x, a[i].y);
if (a[i].z == -1) printf("%d %d 0\n", a[i].x, a[i].y);
}
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!