图论专题-学习笔记:强连通分量
一些 update
update on 2021/8/12:增加了对于 Kosaraju 算法优势的分析。
1. 前言
强连通分量,是图论的一个东西。
这个东西可以将有向图变为一张 DAG,而在 DAG 上就可以使用各种技巧了。
2. 定义
分量的定义:在一张给定的有向图中,如果点 \(a,b\) 能够互相到达,就称点 \(a,b\) 在一个分量中。
显然的,分量具有传递性,即若 \(a,b\) 在一个分量,\(b,c\) 在一个分量,那么 \(a,c\) 也在一个分量。
强连通分量:对于一张图 \(G\),设其点集为 \(V\),如果能够从中选出一些点构成点集 \(V'\),满足 \(V'\) 内的所有点都在一个分量内,且 \(V'\) 内的所有点都不与 \(V'\) 之外的点在一个分量内,那么点 \(V'\) 称作图 \(G\) 的一个强连通分量。
根据定义可以知道,强连通分量里面的所有点都是能够互相到达的。
3. 求法
强连通分量有很多求法,而笔者使用的求法是 Kosaraju 算法,该算法采用两次 dfs 确定强连通分量,也就是俗称的两遍 dfs 求强连通分量。
该算法的步骤如下:
- 首先先对整张图做一遍 dfs(任意点开始均可),对于每一个点,当遍历完其所有出边之后将这个点压入一个栈 \(sta\)。
- 然后将 \(sta\) 反转。
- 从 \(sta\) 的第一个元素开始,建立一张反向图,在反向图中做一遍 dfs,此时从一个点能够遍历到的所有点属于一个强连通分量。
注意第三步是有顺序的,也就是反转 \(sta\) 之后从头开始选择点遍历,每个点只遍历一次。
那么这个算法为什么是正确的呢?
假设反转前的 \(sta=\{a,b,c,...,z\}\)。
那么反转之后 \(z\) 是第一个,假设在反向图中 \(z\) 能到达 \(a,b,c\)。
那么显然的,此时在正向图中能够保证 \(a,b,c\) 能够到达 \(z\)。
但是为什么 \(z\) 能够到达 \(a,b,c\) 呢?
因为在反转前的 \(sta\) 中,\(a,b,c\) 在 \(z\) 前面。
这就意味着 \(a,b,c\) 必须在 \(z\) 之前进栈,而在 \(z\) 之前进栈,要么是 \(a,b,c\) 与 \(z\) 不连通,但是这种情况已经被排除了。
因此,只能是 \(z\) 能够到达 \(a,b,c\),这样才能够说明 \(a,b,c\) 在 \(z\) 前面。
证毕。
关于这一部分的代码可以看应用的缩点代码,这里面包含了强连通分量的代码。
除了 Kosaraju 算法之外,最常用的求强连通分量的算法就是 Tarjan 算法了。
那么 Kosaraju 算法有什么优点呢?
- 思路比 Tarjan 算法简洁易懂。
- 代码不容易出错。
- 有一个很神奇的特性,这个特性将会在应用板块中讲解。
而且特别的,由于求强连通分量的 Tarjan 算法和求割点与桥的 Tarjan 算法在实现细节上是有一定不同的,有些时候容易将两者搞混,因此笔者只讲述 Kosaraju 算法。
4. 应用
强连通分量有 2 个应用,一个是缩点,一个是 2 - SAT,此处只讲缩点。
例题:P3387 【模板】缩点
强连通分量的一个好处是能够将一张有向图变为一张 DAG。
- 怎么变呢?
因为一个强连通分量里面的所有点互相可达,因此我们可以将这些点的信息合并成一个点,那么在这么做之后这张图就会变成一张 DAG。
- 为什么是 DAG?
假设图中还有环,那么这些点就属于一个强连通分量,但是我们已经将所有的强连通分量缩成一个点了,矛盾。
- 缩点有什么用吗?
DAG 最好用的地方就是拓扑排序!利用拓扑排序 + DP,可以解决很多图上问题。
代码:
/*
========= Plozia =========
Author:Plozia
Problem:P3387 【模板】缩点
Date:2021/4/15
========= Plozia =========
*/
#include <bits/stdc++.h>
using std::queue;
typedef long long LL;
const int MAXN = 1e4 + 10, MAXM = 1e5 + 10;
int n, m, val[MAXN], cnt_EEdge = 1, a[MAXN], HHead[MAXN], cnt_Edge = 1, sta[MAXN], Top, col, Color[MAXN], Head[MAXN];
int cnt[MAXN], ans, f[MAXN];
struct node { int to, val, Next; } EEdge[MAXM << 1], Edge[MAXM << 1];
bool vis[MAXN];
int read()
{
int sum = 0, fh = 1; char ch = getchar();
for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = (sum << 3) + (sum << 1) + (ch ^ 48);
return sum * fh;
}
void add_EEdge(int x, int y, int z) { ++cnt_EEdge; EEdge[cnt_EEdge] = (node){y, z, HHead[x]}; HHead[x] = cnt_EEdge; }
void add_Edge(int x, int y, int z) { ++cnt_Edge; Edge[cnt_Edge] = (node){y, z, Head[x]}; Head[x] = cnt_Edge; }
//千万注意不能搞错原图和新图的存储!!!
int Min(int fir, int sec) { return (fir < sec) ? fir : sec; }
int Max(int fir, int sec) { return (fir > sec) ? fir : sec; }
void dfs1(int now)
{
vis[now] = 1;
for (int i = HHead[now]; i; i = EEdge[i].Next)
{
int u = EEdge[i].to;
if (EEdge[i].val == 0) continue;
if (vis[u]) continue; dfs1(u);
}
sta[++Top] = now;//进栈
}
void dfs2(int now, int col)
{
vis[now] = 1; Color[now] = col;//染色,记录是哪一个强连通分量
for (int i = HHead[now]; i; i = EEdge[i].Next)
{
int u = EEdge[i].to;
if (vis[u] || EEdge[i].val == 1) continue;
dfs2(u, col);
}
}
void Topsort()//拓扑排序 + DP
{
queue <int> q;
for (int i = 1; i <= col; ++i)
if (cnt[i] == 0) q.push(i), ans = Max(ans, f[i] = a[i]);
while (!q.empty())
{
int x = q.front(); q.pop();
for (int i = Head[x]; i; i = Edge[i].Next)
{
int u = Edge[i].to; --cnt[u];
f[u] = Max(f[u], f[x] + a[u]);
ans = Max(ans, f[u]);
if (cnt[u] == 0) q.push(u);
}
}
}
int main()
{
n = read(), m = read();
for (int i = 1; i <= n; ++i) val[i] = read();
for (int i = 1; i <= m; ++i)
{
int u = read(), v = read();
add_EEdge(u, v, 1); add_EEdge(v, u, 0);
}
for (int i = 1; i <= n; ++i)
if (!vis[i]) dfs1(i);//一次 dfs
memset(vis, 0, sizeof(vis));
std::reverse(sta + 1, sta + Top + 1);//注意反转!
for (int i = 1; i <= n; ++i)
if (!vis[sta[i]]) { ++col; dfs2(sta[i], col); }//二次 dfs
for (int i = 1; i <= cnt_EEdge; i += 2)
{
int u = EEdge[i ^ 1].to, v = EEdge[i].to;
if (Color[u] != Color[v]) { add_Edge(Color[u], Color[v], 1); cnt[Color[v]]++; }
//建立新图
}
for (int i = 1; i <= n; ++i) a[Color[i]] += val[i];//处理新图的点权
Topsort(); printf("%d\n", ans);
return 0;
}
接下来,在确定理解上述代码之后,讲解 Kosaraju 算法的特性:
- 对于缩点之后的图上的两个点 \(i,j\),如果 \(Color_i < Color_j\),则 \(i\) 一定能够走到 \(j\)。换言之,求出这张图的拓扑序后 \(i\) 在 \(j\) 前面。
为什么会有这样的特性呢?简要证明如下:
首先考虑 3 个点的情况:
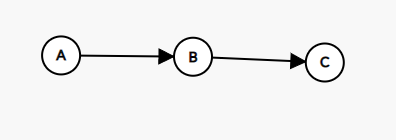
设上图中的 A,B,C 是 3 个强连通分量。
考虑我们第一遍 dfs 时候栈内 A,B,C 的顺序。
假设首先从 A 开始 dfs,那么 \(A \to B \to C\),C 进栈,B 进栈,A 进栈,栈内为 CBA,翻转后为 ABC,取出来做第二遍 dfs 时 \(Color_A < Color_B < Color_C\),结论成立。
如果从 B 开始 dfs,那么 \(B \to C\),C 进栈,B 进栈,然后再次从 A 开始 dfs,A 进栈,栈内同样为 CBA,翻转后同样为 ABC。
此时你会发现上面这段话说明了两件事情:
- 结论的正确性。
- 结论对于任意一种 dfs 的先后顺序都成立。
综合这两点,可以得知在只有 3 个强连通分量的时候结论完全正确。
那么现在推广到一般情况,对于我们缩点后建出的图而言,是一张 DAG,而这张 DAG 上有若干条链,对于每一条链上的所有强连通分量而言,我们可以类比上述 3 个点的证明得知:无论以何种顺序遍历这条链,翻转栈内这些强连通分量的相对顺序始终是按照链上这些强连通分量的相对顺序排序的。
由于 DAG 就是由这些链共节点组成的,对于每条链都满足上述性质,自然整张 DAG 都满足上述性质。
综上,要证明的结论成立。
2 - SAT 问题求一组可行解时需要用到上述结论。
对 2 - SAT 问题感兴趣的可以看一下我的这篇文章:图论专题-学习笔记:2 - SAT 问题
5. 总结
强连通分量定义:对于一张图 \(G\),设其点集为 \(V\),如果能够从中选出一些点构成点集 \(V'\),满足 \(V'\) 内的所有点都在一个分量内,且 \(V'\) 内的所有点都不与 \(V'\) 之外的点在一个分量内,那么点 \(V'\) 称作图 \(G\) 的一个强连通分量。
求法:Kosaraju 算法,采用两遍 dfs,第一遍正向图,第二遍将栈反转后反向图。
应用:缩点与 2-SAT。


