DP专题-专项训练：状压 DP

目录

• 一些 update
• 1. 前言
• 2. 练习题
  • P2704 [NOI2001] 炮兵阵地
  • P2157 [SDOI2009]学校食堂
  • P5005 中国象棋 - 摆上马
• 3. 总结

一些 update

update on 2021/7/19：发现第二道题目的代码贴错了，现已更正。

1. 前言

本篇博文是状压 DP 的练习题博文。

没有学过状压 DP？

传送门：DP专题-学习笔记：状态压缩 DP

状压 DP 非常之灵活，这里选了 3 道经典题。

更多的题目？请前往洛谷用户 @StudyingFather 的 一个动态更新的洛谷综合题单 查看。

2. 练习题

题单：

• P2704 [NOI2001] 炮兵阵地
• P2157 [SDOI2009]学校食堂
• P5005 中国象棋 - 摆上马

P2704 [NOI2001] 炮兵阵地

这道题是一道简单题，相信各位掌握了互不侵犯那题后很容易解决。

设 \(f_{i,j,k}\) 表示 \(1-i\) 行，第 \(i\) 行状态为 \(j\)，第 \(i-1\) 行状态为 \(k\) 的方案数。

那么转移方程如下：

\[f_{i,j,k}=\max\{f_{i-1,k,l}+Sum_j\} \]

保证 \(j,k,l\) 状态合法。

判断状态合法？\((j \& k) || (k \& l) || (l \& j)\)

于是就结束了……

等一等！我 MLE 了！

这也就是在上一篇博文中作者特别提及过的问题。

这道题需要压缩空间。

两种方法：

1. 采用滚动数组的方式，减少第一维的空间。
   因为这道题的转移当前行只和上一行有关系，因此第一位只需要开 2，然后利用 \(i \mod 2\) 来转移即可。
2. 上篇博文中作者提到过，这道题如果我们将合法状态输出，会发现 最多只有 60 个。 所以完全可以直接压缩后两位状态到 60。

当然可以两个一起，但是感觉没什么用处。

代码：

/*
========= Plozia =========
	Author:Plozia
	Problem:P2704 [NOI2001] 炮兵阵地
	Date:2021/3/2
========= Plozia =========
*/

#include <bits/stdc++.h>
#define Max(a, b) ((a > b) ? a : b)

typedef long long LL;
const int MAXN = (1 << 10) + 10, MAXP = 60 + 10;
int n, m, cnt, State[MAXN], Sum[MAXN], a[100 + 10][100 + 10], Map[100 + 10], f[100 + 10][MAXP][MAXP], ans = 0;

int read()
{
	int sum = 0, fh = 1; char ch = getchar();
	for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
	for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = (sum << 3) + (sum << 1) + (ch ^ 48);
	return sum * fh;
}

void dfs(int pos, int sum, int num)
{
	if (pos >= m) {State[++cnt] = sum; Sum[cnt] = num; return ;}
	dfs(pos + 1, sum, num);
	dfs(pos + 3, sum + (1 << pos), num + 1);
}

int main()
{
	n = read(), m = read();
	Map[0] = (1 << m) - 1;
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= m; ++j)
		{
			char ch; std::cin >> ch;
			if (ch == 'P') a[i][j] = 1;
			Map[i] += a[i][j] * (1 << (m - j));
		}
	dfs(0, 0, 0);
	for (int i = 1; i <= cnt; ++i)
		for (int j = 1; j <= cnt; ++j)
			f[1][i][j] = Sum[i];
	for (int i = 2; i <= n; ++i)
	{
		for (int j = 1; j <= cnt; ++j)
		{
			if (!((Map[i] & State[j]) == State[j])) continue;
			for (int k = 1; k <= cnt; ++k)
			{
				if (!((Map[i - 1] & State[k]) == State[k])) continue;
				for (int l = 1; l <= cnt; ++l)
				{
					if (!((Map[i - 2] & State[l]) == State[l])) continue;
					if ((State[j] & State[k]) || (State[k] & State[l]) || (State[j] & State[l])) continue;
					f[i][j][k] = Max(f[i][j][k], f[i - 1][k][l] + Sum[j]);
				}
			}
		}
	}
	for (int i = 1; i <= cnt; ++i)
		for (int j = 1; j <= cnt; ++j)
			ans = Max(ans, f[n][i][j]);
	printf("%lld\n", ans);
	return 0;
}

P2157 [SDOI2009]学校食堂

先补充一个式子：

\[a \text{ or } b \text{ - } a \text{ and } b = a \text{ xor } b \]

不过不知道这个结论好像也可以做

神仙状压 DP 题。

第一眼看上去的时候我傻了：\(1\leq n \leq 1000\).

这怎么状压啊？没法状压啊？

然后我又看了一眼数据：\(0 \leq B_i \leq 7\)。

哦那没事了。

于是我们首先有了一个状态的雏形：\(f_{i,j}\) 表示当前做到第 \(i\) 个人而且 \([1,i-1]\) 的人全部都拿过了饭的最小等待时间，其中当前第 \(i\) 个人以及其后面 7 个人拿饭组成的状态为 \(j\)。

于是你会发现状态转移方程写不出来。

写不出来吗？我们试着写一写：

1. 如果第 \(i\) 个人拿了饭，也就是 \(j \& 1\) 为真，那么此时 \(i\) 就可以走人，直接转移时间到 \(f_{i+1,j>>1}\)。
2. 如果第 \(i\) 个人不拿饭，那么我们需要从后面挑一个人出来拿饭，于是就。。。。。。

你会发现，如果我们不知道上一个拿饭的人是谁，是无法算出转移新增的时间的！

于是我们引入第三维变量 \(k\) 来记录上一个拿饭的人，\(k \in [-8,7]\) 表示距离 \(i\) 的位置，也就是上一个拿饭的人是 \(i+k\)。

那么再次写转移方程：

1. 如果第 \(i\) 个人拿了饭，也就是 \(j \& 1\) 为真，那么此时 \(i\) 就可以走人，直接转移时间到 \(f_{i+1,j>>1,k-1}\)。
2. 如果第 \(i\) 个人不拿饭，也就是 \(j \& 1\) 为假，此时我们需要从后面挑一个人出来拿饭，假设这个人是 \(i+l\)，那么他将影响到的是 \(f_{i,j|(1<<l),l}\)。
   什么意思呢？由于第 \(i\) 个人不拿饭，那么没法转移到第 \(i+1\)，但是第 \(l\) 个人先拿了饭，此时的状态就会变成 \(j|(1<<l)\)，上一个人编号为 \(i+l\)。
   但是需要注意的是，考虑到 \(i\) 后面的人可能会有更小的容忍值，那么此时我们需要变量 \(r\) 来记录当前最多能够使谁拿饭（也就是编号最大的），如果超出这个值就说明有人不能容忍了，要立刻停止转移。

初值：\(f_{1,0,0}=0\)，其余为正无穷。答案：\(\min\{f_{n+1,0,i}|i \in [-8,0]\}\)。

需要注意的是，考虑到数组维度不能开负数，\(k\) 都要加 8，而这就导致了很多细节性的问题，需要注意。

代码：

#include <bits/stdc++.h>
#define Min(a, b) ((a < b) ? a : b)
using namespace std;

typedef long long LL;
const int MAXN = 1000 + 10, MAXP = (1 << 8) - 1;
int n, t[MAXN], b[MAXN], f[MAXN][MAXP][20];

int read()
{
	int sum = 0, fh = 1; char ch = getchar();
	for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
	for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = (sum << 3) + (sum << 1) + (ch ^ 48);
	return (fh == 1) ? sum : -sum;
}

namespace Plozia
{
	void main()
	{
		n = read();
		memset(t, 0, sizeof(t)); memset(b, 0, sizeof(b));
		for (int i = 1; i <= n; ++i) t[i] = read(), b[i] = read();
		memset(f, 0x3f, sizeof(f));
		f[1][0][7] = 0;
		for (int i = 1; i <= n; ++i)
			for (int j = 0; j <= MAXP; ++j)
				for (int k = -8; k <= 7; ++k)
				{
					if (f[i][j][k + 8] != 0x3f3f3f3f)
					{
						if (j & 1) f[i + 1][j >> 1][k - 1 + 8] = Min(f[i + 1][j >> 1][k - 1 + 8], f[i][j][k + 8]);
						else
						{
							int r = 0x3f3f3f3f;
							for (int l = 0; l <= 7; ++l)
							{
								if ((j >> l) & 1) continue;
								if (i + l > r) break;
								r = Min(r, i + l + b[i + l]);
								f[i][j | (1 << l)][l + 8] = Min(f[i][j | (1 << l)][l + 8], f[i][j][k + 8] + ((i + k) ? (t[i + k] ^ t[i + l]) : 0));
							}
						}
					}
				}
		int ans = 0x3f3f3f3f;
		for (int i = 0; i <= 8; ++i)
			ans = Min(ans, f[n + 1][0][i]);
		printf("%d\n", ans);
		return ;
	}
}

int main()
{
	int t = read();
	while (t--) Plozia::main();
	return 0;
}

P5005 中国象棋 - 摆上马

相信自己的做法，大喊一声 ：I won't MLE！你就会过这道题。

于是我就 MLE 了。

先假设空间限制为 256 MB，然后来想这道题。

这是一道二维的状压 DP，模仿第一题不难想到设 \(f_{i,j,k}\) 表示当前做到第 \(i\) 行，当前行状态为 \(j\)，上一行状态为 \(k\) 的方案数。

因为马攻击范围可以到上下两行，所以需要枚举上上行状态 \(l\)。

那么转移方程如下：

\[f_{i,j,k}=\sum f_{i-1,k,l} \]

其中保证 \(j,k,l\) 不会互相冲突。

初值：\(f_{1,i,0}=1\)，第二行需要特别处理，因为没有上上行。

于是我们可以先写下面这样的代码：

for (int i = 0; i < (1 << m); ++i)
		for (int j = 0; j < (1 << m); ++j)
			if (i 与 j 不冲突) f[2][j][i] = (f[2][j][i] + f[1][i][0]) % P;
for (int i = 3; i <= n; ++i)
	for (int j = 0; j < (1 << m); ++j)
		for (int k = 0; k < (1 << m); ++k)
		{
			f[i][j][k] = 0;
			if (j 与 k 冲突) continue;
			for (int l = 0; l < (1 << m); ++l)
			{
				if (k 与 l 冲突) continue;
				if (j 与 l 冲突) continue;
				f[i][j][k] = (f[i][j][k] + f[i - 1][k][l]) % P;
			}
		}
ans = 0;
for (int i = 0; i < (1 << m); ++i)
	for (int j = 0; j < (1 << m); ++j)
		if (i 与 j 不冲突) ans = (ans + f[n][i][j]) % P;

然后来考虑怎么处理冲突问题。

冲突分两种：两行冲突（Two_attack）和三行冲突（Three_attack）。

• 两行冲突：也就是单行对下一行的攻击是否与下一行冲突。
• 三行冲突：也就是第一行的跨行攻击是否对第三行冲突。

不好理解？那就对了，反正我说的也不是人话， 上图！

两行冲突：

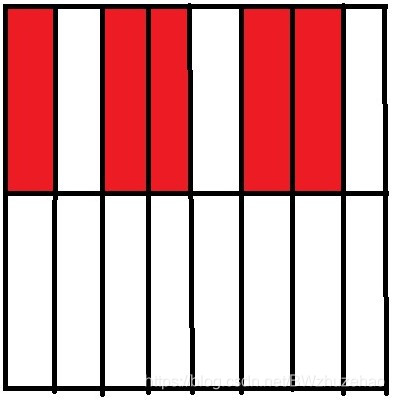
从右往左考虑。记当前状态为 10110110

第一个格子没有马，跳过。

第二个格子有马，那么这个格子右边有马吗？没有。于是可以向右攻击。但是他左边有马，于是不能向左攻击。

那么就变成了这样：

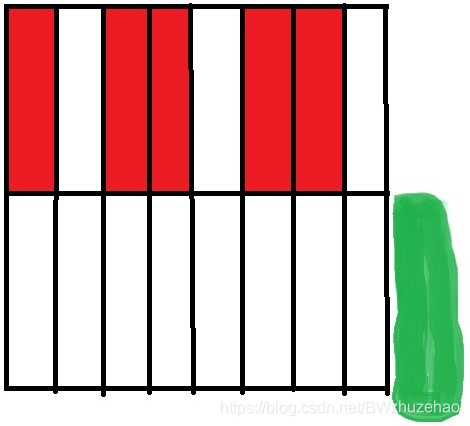
第三个格子，右边有马，左边没有马，那么可以向左边攻击。

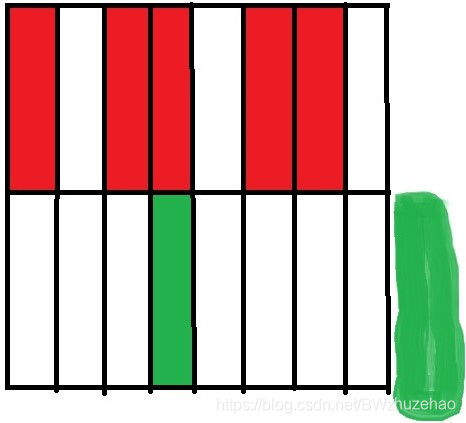
这么循环反复，最后就变成了这样：

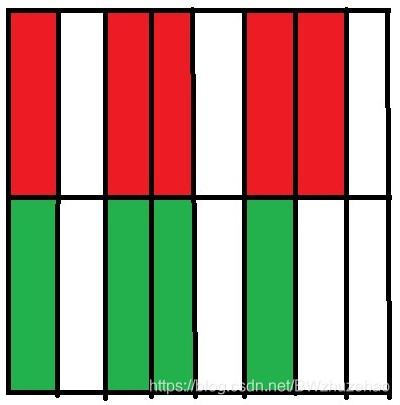
三行冲突（暂且不考虑两行冲突）：

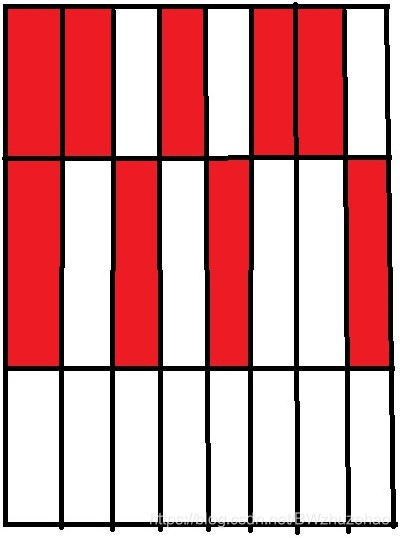
还是考虑第一行，发现右数第二格有马，而且没被挡住，那么可以向下面两行攻击。

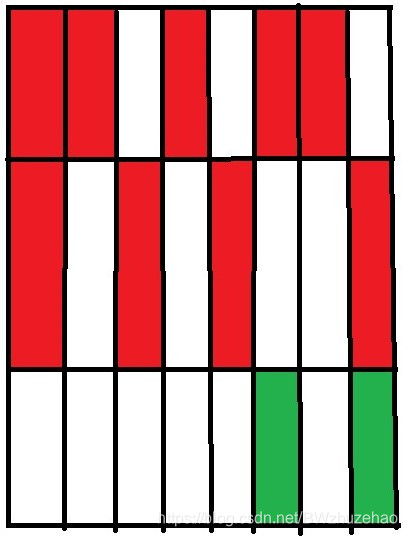
然后右数第三个，有马且没被挡住，可以向下攻击。

那么继续做下去，发现只有第一列的马被挡住，那么最后结果如下：

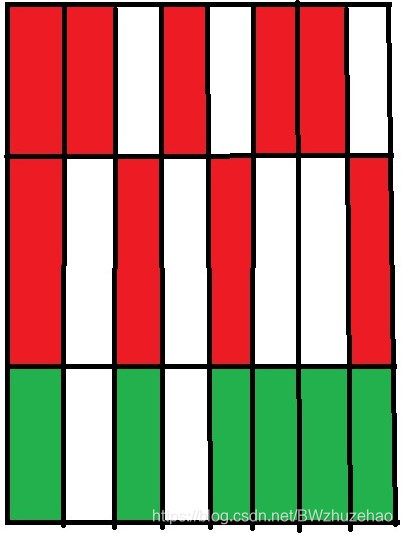
于是就做完了。

关于代码实现：

首先我们需要两个基础函数：

int Getbit(int x, int a)//返回 x 的二进制下第 a 位且保留右侧 0
{
	if (a < 1) return 0;
	return x & (1 << (a - 1));
}

int check(int x, int a)//查询 x 的二进制下第 a 位
{
	if (a < 1) return 0;
	if (x & (1 << (a - 1))) return 1;
	return 0;
}

然后就可以愉快的打代码了。

这里有一个小技巧：-1 的补码是 11111111111111111111111111111111（32 个1），可以利用这个来处理位运算。

Two_attack 和 Three_attack 如下：

int Two_attack(int k)//k 是上面一行状态
{
	int State = 0;
	for (int i = 1; Getbit(-1, i) <= k; ++i)
	{
		if (!check(k, i)) continue;
		if (!check(k, i - 1)) State |= Getbit(-1, i - 2);
		if (!check(k, i + 1)) State |= Getbit(-1, i + 2);
	}
	return State;
}

int Three_attack(int k, int l)//k 是第一行，l 是第二行
{
	int State = 0;
	for (int i = 1; Getbit(-1, i) <= k; ++i)
	{
		if (!check(k, i)) continue;
		if (!check(l, i)) State |= Getbit(-1, i - 1), State |= Getbit(-1, i + 1);
	}
	return State;
}

那么就做完了。

特别提醒：因为本题毒瘤的空间限制，必须使用滚动数组压缩空间。

代码：

/*
========= Plozia =========
	Author:Plozia
	Problem:P5005 中国象棋 - 摆上马
	Date:2021/3/5
========= Plozia =========
*/

#include <bits/stdc++.h>

typedef long long LL;
const int P = 1e9 + 7;
int n, m;
LL f[3][64][64], ans;

int read()
{
	int sum = 0, fh = 1; char ch = getchar();
	for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
	for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = (sum << 3) + (sum << 1) + (ch ^ 48);
	return (fh == 1) ? sum : -sum;
}

int Getbit(int x, int a)//返回 x 的二进制下第 a 位且保留右侧 0
{
	if (a < 1) return 0;
	return x & (1 << (a - 1));
}

int check(int x, int a)//查询 x 的二进制下第 a 位
{
	if (a < 1) return 0;
	if (x & (1 << (a - 1))) return 1;
	return 0;
}

int Two_attack(int k)//k 是上面一行状态
{
	int State = 0;
	for (int i = 1; Getbit(-1, i) <= k; ++i)
	{
		if (!check(k, i)) continue;
		if (!check(k, i - 1)) State |= Getbit(-1, i - 2);
		if (!check(k, i + 1)) State |= Getbit(-1, i + 2);
	}
	return State;
}

int Three_attack(int k, int l)//k 是第一行，l 是第二行
{
	int State = 0;
	for (int i = 1; Getbit(-1, i) <= k; ++i)
	{
		if (!check(k, i)) continue;
		if (!check(l, i)) State |= Getbit(-1, i - 1), State |= Getbit(-1, i + 1);
	}
	return State;
}

int main()
{
	n = read(), m = read();
	for (int i = 0; i < (1 << m); ++i) f[1][i][0] = 1;
	for (int i = 0; i < (1 << m); ++i)
		for (int j = 0; j < (1 << m); ++j)
			if ((!(Two_attack(i) & j)) & (!(Two_attack(j) & i))) f[2][j][i] = (f[2][j][i] + f[1][i][0]) % P;
	for (int i = 3; i <= n; ++i)
		for (int j = 0; j < (1 << m); ++j)
			for (int k = 0; k < (1 << m); ++k)
			{
				f[i % 3][j][k] = 0;
				if (Two_attack(j) & k) continue;
				if (Two_attack(k) & j) continue;
				for (int l = 0; l < (1 << m); ++l)
				{
					if (Two_attack(l) & k) continue;
					if (Two_attack(k) & l) continue;
					if (Three_attack(l, k) & j) continue;
					if (Three_attack(j, k) & l) continue;
					f[i % 3][j][k] = (f[i % 3][j][k] + f[(i - 1) % 3][k][l]) % P;
				}
			}
	ans = 0;
	for (int i = 0; i < (1 << m); ++i)
		for (int j = 0; j < (1 << m); ++j)
			if ((!(Two_attack(i) & j)) & (!(Two_attack(j) & i))) ans = (ans + f[n % 3][i][j]) % P;
	printf("%lld\n", ans);
	return 0;
}

3. 总结

状压 DP 还是非常灵活的，非常考验思维能力以及代码能力，需要多加练习。