字符串专题-学习笔记：KMP
1.概述
KMP 算法是一种字符串算法，具体解决的问题为字符串匹配问题：
给出一个模式串 \(t\)，文本串 \(s\)，请问 \(t\) 是否为 \(s\) 的字串 / \(t\) 在 \(s\) 中出现了几次等等问题。
后文中无特殊说明，\(n\) 为文本串 \(s\) 的长度，\(m\) 为模式串 \(t\) 的长度。
2.例题
我们要求两个东西：
- 模式串 \(t\) 在文本串 \(s\) 中出现的位置。
- 模式串 \(t\) 的 \(border\) 长度。
我们暂且先不管这个 \(border\)，考虑第 1 个问题。
显然有一种暴力匹配的方法：直接从最前面的位置开始，在文本串 \(s\) 中截出长度为 \(m\) 的字串，\(O(m)\) 暴力匹配。
然而，这样做会发现最坏理论复杂度到了 \(O(nm)\)！我们不能忍受。
于是 KMP 就出现了。
比如面对这样的两个字符串：
文本串 s = a a a b a c a b a c d
模式串 t = a b a
规定起始点为 \(i\)。
如上所示，假设我们现在匹配到了 \(i = 2\) 的位置。我们发现不匹配（失配），那么如果是暴力做法，那么在 \(i = 3\) 的位置就会重新匹配一次。
但是我们完全可以不用这么做，因为 模式串 \(t\) 的前面两个字符跟文本串 \(s\) 的前面两个字符相同，可以直接从第 3 位开始匹配。
而 KMP 的任务就是尽可能多的实现上面这句话。
那么我们又怎么判断要跳到哪里呢？
还记得 \(border\) 吗？\(border\) 可以帮助我们判断要跳到哪里。
比如说我们现在在文本串第 \(i\) 个位置开始匹配，结果失配了，假设失配位置为 \(j\)，那么我们直接从 \(border_j\) 开始匹配。
下文记 \(Next_i\) 为 \(border_i\)。
想想为什么？\(border\) 的定义是：在一个字符串 \(s\) 中，如果一个串 \(str\) 满足其既是 \(s\) 的前缀，又是 \(s\) 的后缀，那么 \(str\) 就是 \(s\) 的一个 \(border\)，而一个串的 \(border\) 指他的所有 \(border\) 的最长长度。
那么如果模式串 \(t\) 失配，我们可以跳到 \(Next_t\) 这个位置继续匹配，而不需要直接从头匹配。
那么如何求 \(Next\) 数组呢？
2.1 自匹配操作
求 \(Next\) 数组在 KMP 中称为自匹配操作。
比如对于模式串 \(\text{t = a b a b a c a b a}\)，我们要对其进行自匹配操作。
注意：\(Next_i=i\) 是没有意义的！
首先显然的，\(Next_1=0\)。
那么 \(Next_2\) 呢？还是等于 0。
\(Next_3\)？等于 1。
但是我们是怎么知道 \(Next_3\) 等于 1 的呢？上图！
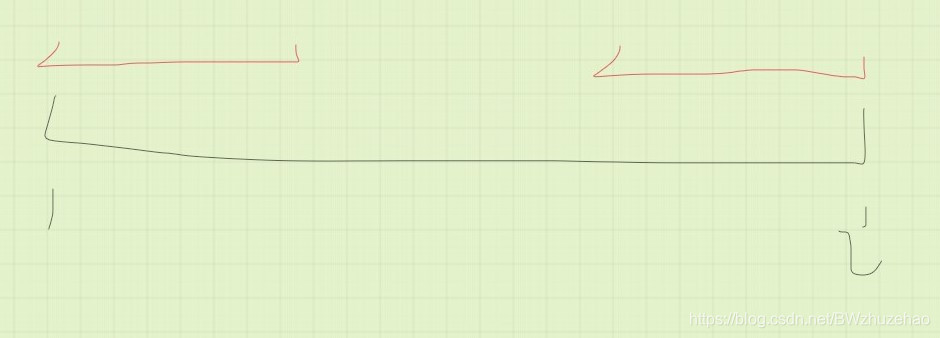
比如我们要求 \(Next_i\)，而此时我们已经保证 \(Next_{1...i-1}\) 已经求好。
上图中红色部分表示这个串的 \(border\)。
设 \(Next_{i-1}=j\)，那么我们假设 \(j\) 在这个位置：
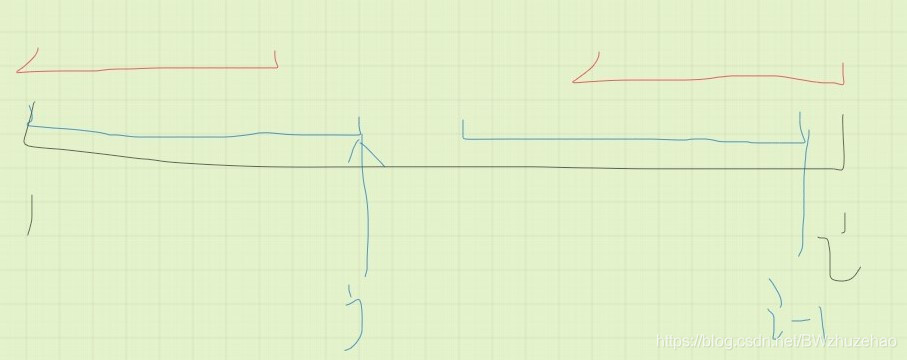
由于上图中两个蓝色部分完全相同，那么我们首先判断一下 \(t_{j +1}\) 跟 \(t_i\) 是否相同，如果相同 \(Next_i\) 就求出来了。
但是不相同呢？或许有的人会说了：那不是还要暴力查找吗？
不需要！因为 \(Next_{i-1}=j\)，此时如果我们再取 \(k=Next_j\)（为了方便擦去了红色部分）：
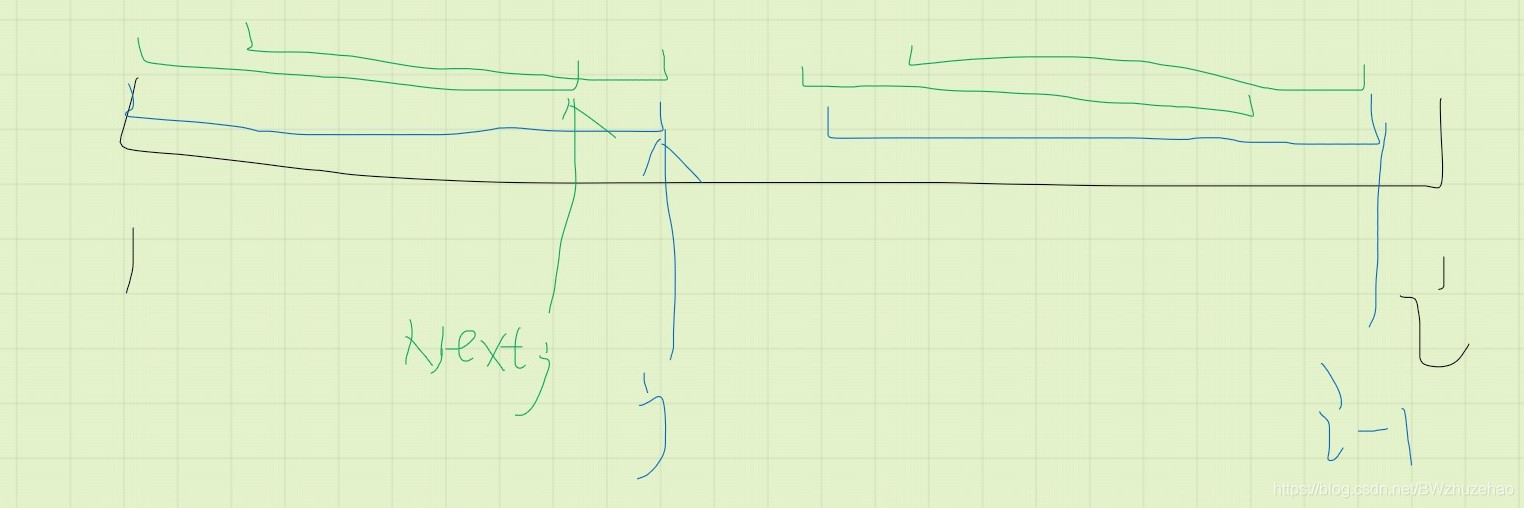
图很丑（确信
那么首先在 \([1,j]\) 内两段绿色字符串相等，而由于 \(Next_{i-1}=j\)，根据传递性，\([1,k]\) 就会跟 \([i-k,i-1]\) （也就是最后这段绿色的）相同，此时我们只需要判断 \(t_{k+1}\) 是否等于 \(t_i\) 就可以了。相同就结束，不相同？继续这么做呗！
所以我们会发现，实质上 KMP 充分利用了 \(border\) 的性质，以 \(Next\) 数组为媒介，减少了转移次数，从而降低时间复杂度。
不过需要注意：当 \(j\) 跳到 0 时，如果 \(t_1 \ne t_i\)，此时 \(Next_i = 0\)；否则其余所有情况，\(Next_i = j + 1\)。
那么在 \(\text{t = a b a b a c a b a}\) 中，\(Next_3=1\) 也就不难想了吧！
对于这个文本串 \(t\) ，\(Next=\{0,0,1,2,3,0,1,2,3\}\)。
于是自匹配操作漂亮解决。
代码：
int j = 0;//初始化为 0
for (int i = 2; i <= m; ++i)
{
while (j && s2[j + 1] != s2[i]) j = Next[j];//不断往前找
if (s2[j + 1] == s2[i]) ++j;//注意 +1
Next[i] = j;
}
其实此时你会发现，题目要求的 \(border\) 长度就是我们的 \(Next\) 数组。
2.2 字符串的匹配
那么回到我们的问题：求模式串 \(t\) 在文本串 \(s\) 内分别出现在哪几个位置。
现在有了 \(Next\) 数组，再加上我们前面说的，应该不难想了。
首先我们先初始化 \(j=0\)，然后开始暴力匹配。
当我们发现 \(t_{j+1}=s_i\) 时，匹配成功，\(j\) 右移。
否则，\(t\) 和 \(s\) 失配，此时根据我们最开始所说的，我们将 \(j\) 重置为 \(Next_j\) 继续匹配。
当完全匹配到一个字符串时，我们输出位置 并且重置 \(j=Next_j\)。（这点非常重要！否则在下一个位置匹配的时候 \(j\) 会被重置为一些奇奇怪怪的东西，导致操作失误，想知道的读者可以自己尝试）
那么这就是 KMP 的字符串匹配过程。
代码：
j = 0;
for (int i = 1; i <= n; ++i)
{
while (j && s2[j + 1] != s1[i]) j = Next[j];//不相同就跳
if (s2[j + 1] == s1[i]) ++j;//注意 +1
if (j == m) {printf("%d\n", i - m + 1); j = Next[j];}//一定要重置！
}
2.3 时间复杂度分析
KMP 的时间复杂度有一点迷。
在随机数据下：
对于每一个 \(i\) 位置，我们在匹配字符串时（包括自匹配）正常情况下 \(j++\) 只会执行一次，那么 \(i\) 从 1 到 \(n\)，\(j\) 从 1 到 \(m\)，互不干扰，时间复杂度为 \(O(n+m)\)。
但是很遗憾的是据说 KMP 比较容易被卡成 \(O(nm)\) 的时间复杂度，不过作者目前还没有找到 hack 数据。
还是 hash 好，稳定的 O(n) 算法
2.4 代码
话说上面都放出来了还有必要再放一遍吗
代码：
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int MAXN = 1e6 + 10;
int n, m, Next[MAXN];
char s1[MAXN], s2[MAXN];
int read()
{
int sum = 0, fh = 1; char ch = getchar();
while (ch < '0' || ch > '9') {if (ch == '-') fh = -1; ch = getchar();}
while (ch >= '0' && ch <= '9') {sum = (sum << 3) + (sum << 1) + (ch ^ 48); ch = getchar();}
return sum * fh;
}
int main()
{
scanf("%s", s1 + 1);
scanf("%s", s2 + 1);
n = strlen(s1 + 1); m = strlen(s2 + 1);
int j = 0;//初始化为 0
for (int i = 2; i <= m; ++i)
{
while (j && s2[j + 1] != s2[i]) j = Next[j];//不断往前找
if (s2[j + 1] == s2[i]) ++j;//注意 +1
Next[i] = j;
}
j = 0;
for (int i = 1; i <= n; ++i)
{
while (j && s2[j + 1] != s1[i]) j = Next[j];//不相同就跳
if (s2[j + 1] == s1[i]) ++j;//注意 +1
if (j == m) {printf("%d\n", i - m + 1); j = Next[j];}//一定要重置！
}
for (int i = 1; i <= m; ++i) printf("%d ", Next[i]);
printf("\n"); return 0;
}
3.总结
KMP 的思想其实就是充分利用各个前后缀之间的关系，使得我们在字符串失配的时候不至于从头开始匹配，从而大大降低时间复杂度。
